Diedro
| Diedro | ||
|---|---|---|
 Imagen del sólido | ||
| Caras | 2 n-gónos | |
| Aristas | n | |
| Vértices | n | |
| Grupo de simetría | Dnh, [2,n], (*22n), orden 4n | |
| Poliedro dual | Hosoedro n-gonal regular | |
| Símbolo de Schläfli | {n,2} | |
| Símbolo de Wythoff | 2 | n 2 | |
| Símbolo de Coxeter-Dynkin |
| |
Un diedro es un tipo de poliedro formado por dos caras poligonales que comparten el mismo conjunto de n aristas. En el espacio euclidiano tridimensional, es degenerado si sus caras son planas, mientras que en el espacio esférico tridimensional, un diedro con caras planas puede considerarse como una lente, un ejemplo de lo que es el dominio fundamental de un espacio lente L(p,q).[1]
Como teselado esférico, puede existir un diedro como forma no degenerada, con dos caras de n lados que cubren la esfera, siendo cada cara una semiesfera, y los vértices en un gran círculo. Es regular si los vértices están igualmente espaciados.
El dual de un diedro n-gonal es un hosoedro n-gonal, en el que n caras del dígono comparten dos vértices.
Etimología
[editar]El término diedro procede de la palabra griega δίεδρος (díedros) y significa "dos lados". Es un polígono regular (triángulo, cuadrado...) que tiene una cara frontal y una cara posterior. En la serie de los poliedros es el caso especial plano más simple.
La expresión se usa dentro de teoría de grupos como grupo diedral y también en la descripción del ángulo entre dos superficies, que se conocen como ángulo diedro.
En cristalografía, se llaman formas cristalinas no cerradas, que constan de dos superficies con un borde común. Estas formas se denominan domos (δῶμα "casa") si las dos superficies están reflejadas entre sí, o esfenoides (σφήν "cuña") cuando se fusionan mediante dos operaciones de simetría. El domo es la forma superficial general (y homónima) de la clase monoclínica (grupo puntual de clase m), mientras que el esfenoide define la clase monoclínico-esfenoidal (de clase 2).[2]
-
Diedros monoclínicos: esfenoide de forma saliente (izquierda) y domo con forma cóncava (derecha)
-
Ángulo diedro, como el ángulo formado entre dos planos
Como poliedro de caras planas
[editar]Un diedro puede considerarse un prisma degenerado cuyas bases son polígonos planos de dos caras que están conectadas "espalda con espalda", de modo que el objeto resultante no tiene profundidad. Los polígonos deben ser congruentes, pero pegados de tal manera que uno sea la imagen especular del otro. Esto se aplica solo si la distancia entre las dos caras es cero; para una distancia mayor que cero, las caras son polígonos infinitos (un poco como las caras digonales del hosoedro apeirogonal, que tienen un ancho mayor que cero y son franjas infinitas).
Los diedros se pueden deducir del teorema de unicidad de Aleksándrov, que caracteriza las distancias en la superficie de cualquier poliedro convexo como localmente euclidianas, excepto en un número finito de puntos con defecto angular positivo sumando 4π. Esta caracterización es válida también para las distancias en la superficie de un diedro, por lo que el enunciado del teorema de Aleksándrov requiere que los diedros se consideren poliedros convexos.[3]
Algunos diedros pueden surgir como miembros del límite inferior de otras familias de poliedros: un prisma con bases digonales sería un diedro cuadrado y una pirámide con una base digonal sería un diedro triangular.
Un diedro regular, con el símbolo de Schläfli {n, 2}, está formado por dos polígonos regulares, cada uno con Símbolo de Schläfli {n}.[4]
Como teselado de la esfera
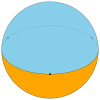
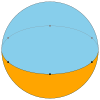
[editar]Un diedro esférico está formado por dos polígonos esféricos que comparten el mismo conjunto de n vértices, en un círculo máximo ecuatorial; cada polígono de un diedro esférico llena una semiesfera.
Un diedro esférico regular está formado por dos polígonos esféricos regulares que comparten el mismo conjunto de n vértices, igualmente espaciados en un círculo máximo ecuatorial.
El poliedro regular {2,2} es auto-dual, y es tanto un hosoedro como un diedro.
| Espacio | Esférico | Euclídeo | ||||||
|---|---|---|---|---|---|---|---|---|
| Nombre del teselado | (Hengonal) Monógono |
Diedro | (Triangular) Diedro |
(Tetragonal) Diedro cuadrado |
Diedro | Diedro | ... | Diedro apeirogonal |
| Imagen del teselado | 
|

|
|

|

|
|
... | 
|
| Símbolo de Schläfli | {1,2} | {2,2} | {3,2} | {4,2} | {5,2} | {6,2} | ... | {∞,2} |
| Diagrama de Coxeter-Dynkin | ... | |||||||
| Caras | 2 {1} | 2 {2} | 2 {3} | 2 {4} | 2 {5} | 2 {6} | ... | 2 {∞} |
| Aristas y vértices | 1 | 2 | 3 | 4 | 5 | 6 | ... | ∞ |
| Configuración de vértices | 1.1 | 2.2 | 3.3 | 4.4 | 5.5 | 6.6 | ... | ∞.∞ |
Diedro apeirogonal
[editar]Cuando n tiende a infinito, un diedro n-gonal se convierte en un diedro apeirogonal como una teselación bidimensional:
Dítopos
[editar]Un dítopo regular es un análogo n dimensional de un diedro, con el símbolo de Schläfli {p, ..., q, r, 2}. Tiene dos facetas, {p, ..., q, r}, que tienen todas sus crestas, {p, ..., q} en común.[5]
Véase también
[editar]Referencias
[editar]- ↑ Gausmann, Evelise; Lehoucq, Roland; Luminet, Jean-Pierre; Uzan, Jean-Philippe; Weeks, Jeffrey (7 de diciembre de 2001). «Topological Lensing in Spherical Spaces». Classical and Quantum Gravity 18 (23): 5155-5186. ISSN 0264-9381. doi:10.1088/0264-9381/18/23/311. Consultado el 27 de diciembre de 2021.
- ↑ Hans-Joachim Bautsch, Will Kleber, Joachim Bohm (1998). Oldenbourg Wissenschaftsverlag, ed. Einführung in die Kristallographie (Introducción a la cristalografía). p. 56.}}
- ↑ O'Rourke, Joseph (2010), On flat polyhedra deriving from Alexandrov's theorem, Bibcode:2010arXiv1007.2016O, arXiv:1007.2016.
- ↑ Coxeter, H. S. M. (January 1973), Regular Polytopes (3rd edición), Dover Publications Inc., p. 12, ISBN 0-486-61480-8.
- ↑ McMullen, Peter; Schulte, Egon (December 2002), Abstract Regular Polytopes (1st edición), Cambridge University Press, p. 158, ISBN 0-521-81496-0.


