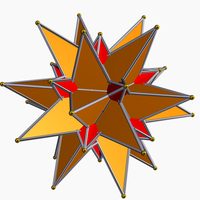
Compuesto de gran dodecaedro estrellado y gran icosaedro
| Compuesto de gran dodecaedro estrellado y gran icosaedro | |
|---|---|
| |
| Tipo | Estelación y compuesto |
| Diagrama de Coxeter-Dynkin |     ∪
|
| Envolvente convexa | Dodecaedro |
| Poliedros | 1 gran icosaedro 1 gran dodecaedro estrellado |
| Caras | 20 triángulos 12 estrellas pentagonales |
| Aristas | 60 |
| Vértices | 32 |
| Grupo de simetría | Icosaédrica (Ih) |
Existen dos formas diferentes del compuesto de gran dodecaedro estrellado y gran icosaedro: uno es un poliedro compuesto y una estelación del gran icosidodecaedro; y el otro es una estelación del icosidodecaedro.[1]
Compuesto dual[editar]
Puede verse como un poliedro compuesto de un gran icosaedro y un gran dodecaedro estrellado. Es uno de los cinco compuestos construidos a partir de sólidos platónicos o de sólidos de Kepler-Poinsot, y sus duales. Es un estelación del gran icosidodecaedro.
Tiene simetría icosaédrica (Ih) y presenta la misma disposición de vértices que el gran triacontaedro rómbico.
Puede verse como uno de los dos equivalentes tridimensionales del compuesto de dos pentagramas ("decagrama" {10/4}). Esta serie continúa en la cuarta dimensión con los compuestos de 4-politopos estrellados.
Estelación del icosidodecaedro[editar]
Este poliedro es una estelación del icosidodecaedro, y como tal figura en el índice de modelos de Wenninger con el número 61. Tiene la misma disposición de vértices que un triacontaedro rómbico, su envolvente convexa.
Las facetas de la estelación para su construcción son:
 Facetas trinagulares |
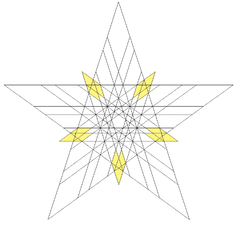 Facetas pentagonales |
Véase también[editar]
- Compuesto de dos tetraedros
- Compuesto de cubo y octaedro
- Compuesto de dodecaedro e icosaedro
- Compuesto de pequeño dodecaedro estrellado y gran dodecaedro
Referencias[editar]
- ↑ Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9., pág. 90.
Bibliografía[editar]
- Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 0-521-54325-8., págs. 51-53.
- Martyn Cundy and A. Rollett. "Great Icosahedron Plus Great Stellated Dodecahedron". §3.10.4 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 132-133, 1989.
Enlaces externos[editar]
- Weisstein, Eric W. «Great Icosahedron-Great Stellated Dodecahedron Compound». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Gran dodecaedro estrellado más gran icosaedro - modelo de papel metálico
- VRML George Hart: modelo transparente VRML
| Control de autoridades |
|
|---|
Datos: Q5156874