Disposición de vértices
En geometría, una disposición de vértices es un conjunto de puntos en el espacio descritos por sus posiciones relativas. Pueden ser caracterizados por su uso en politopos.
Por ejemplo, una disposición de vértices cuadrada se entiende como cuatro puntos en un plano, con ángulos y distancias iguales respecto a un punto central.
Dos politopos comparten la misma disposición de vértices si comparten el mismo N-esqueleto.
Disposición de vértices[editar]
El mismo conjunto de vértices puede ser conectado por lados o aristas de maneras diferentes. Por ejemplo, el pentágono y pentagrama tienen la misma disposición de vértices, mientras que el segundo conecta los vértices alternadamente.
 Pentágono
|
 Pentagrama
|
Una disposición de vértices es a menudo descrita por la envolvente convexa del politopo que la contiene. Por ejemplo, el pentagrama regular puede decirse que tiene una disposición de vértices pentagonal (regular).
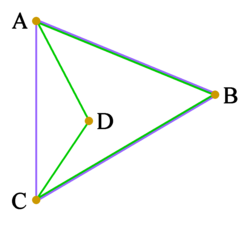
|
ABCD Es un cuadrilátero cóncavo (verde). Su disposición de vértices es el conjunto {A, B, C, D}. Su envolvente convexa es el triángulo ABC (azul). La disposición de vértices de la envolvente convexo es el conjunto {A, B, C}, que no coincide con el cuadrilátero; en este caso, la envolvente convexa no es una manera adecuada de describir la disposición de vértices. |
Recubrimientos teselados infinitos también pueden compartir disposiciones de vértices comunes.
Por ejemplo, este enrejado triangular de puntos puede ser conectado para formar distintas distribuciones de triángulos isósceles o de caras rómbicas.
 Puntos de enrejado |
 Teselado triangular |
 Teselado rómbico |
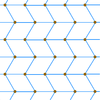 en Zig-zag |
 hexagonal |
Disposición de aristas[editar]
Los poliedros también pueden compartir una disposición de aristas difiriendo en la configuración de sus caras.
Por ejemplo, el gran dodecaedro (con caras cruzadas) comparte su disposición de aristas con el icosaedro convexo:
 Icosaedro (20 triángulos) |
 Gran dodecaedro (12 pentágonos cruzados) |
Disposición de caras[editar]
Los politopos de cuatro dimensiones también pueden tener la misma disposición de caras, lo que significa que tienen similares vértices, aristas, y disposición de caras, pero puede diferir en sus células tridimensionales.
Por ejemplo, del diez-no convexo-regular politopo de Schläfli-Hess, hay sólo 7 únicas disposiciones de caras distintas.
Por ejemplo, el gran estrellado de 120-células y el mayor estrellado de 120-células, ambos con caras pentagrámicas, aparece visualmente indistinguible sin una representación de sus células:
 Gran estrellado de 120-células (120 pequeño dodecaedro estrellado) |
 Mayor estrellado de 120-células (120 mayor dodecaedro estrellado) |
Clases de politopos similares[editar]
George Olshevsky defiende el término de regimiento para designar un conjunto de politopos que comparten una disposición de lados, y de forma generalizada, n-regimiento para un conjunto de politopos cuyos elementos comparten disposición de elementos hasta la dimensión n. Sinónimos para casos especiales incluyen los términos de compañía para un 2-regimiento (compartiendo caras) y ejército para un 0-regimiento (compartiendo vértices).
