Cardán

Modelo esquemático de una junta cardán.

El cardán es un sistema mecánico, descrito por primera vez por Girolamo Cardano, que permite unir dos ejes no coaxiales (es decir, que cada eje no se encuentra en la misma línea que el otro). Su objetivo es transmitir el movimiento de rotación desde un eje conductor a otro conducido a pesar de no ser colineales.​

Frente a otro tipo de articulaciones tiene la característica de ser una junta no homocinética; es decir, el eje al que se transmite el movimiento no gira a una velocidad angular constante. La relación de transmisión instantánea oscila alrededor de la unidad, generando en el eje conducido una aceleración y un retraso por cada medio giro, cuya intensidad aumenta en función del ángulo formado por los árboles. Esta característica debe ser gestionada adecuadamente pues de lo contrario se producirían vibraciones susceptibles de destruir los sistemas donde se utilicen.​

Cuando es necesario proporcionar una velocidad de salida constante se utilizan juntas homocinéticas, cuyo tipo más simple está constituido precisamente por dos juntas cardánicas acopladas a un cuerpo común. Este sistema de doble cardán permite que los cambios instantáneos de la velocidad angular trasmitidos al cuerpo común por uno de los cardanes sean compensados en sentido contrario por el otro, de manera que las velocidades angulares instantáneas de los árboles de entrada y salida sean iguales en todo momento, aunque el eje central estará sometido a constantes aceleraciones y deceleraciones. Las juntas homocinéticas Glaencer-Spicer también utilizan un sistema compacto de doble cardán.​

Historia

Diseño clásico de una junta universal o cardán.

El concepto principal de la junta universal se basa en el diseño de la suspensión cardán, que se ha utilizado desde la antigüedad. Un precedente de la articulación universal fue su uso por los antiguos griegos en la balista.​ En Europa, la articulación universal a menudo se denomina junta cardánica, o eje de transmisión cardán, en referencia al matemático italiano Girolamo Cardano, que, sin embargo, en sus escritos, mencionó solo montajes de cardán, no articulaciones universales.​

El mecanismo fue descrito más tarde en Technica curiosa sive mirabilia artis (1664) por Gaspar Schott, quien erróneamente afirmó que era una junta homocinética.​​​ Poco después, entre 1667 y 1675, Robert Hooke analizó la unión y descubrió que su velocidad de rotación no era uniforme, pero esta propiedad se podía usar para seguir el movimiento de la sombra en la cara de un reloj de sol.​ De hecho, la componente de la ecuación de tiempo que explica la inclinación del plano ecuatorial relativo a la eclíptica es completamente análogo a la descripción matemática de la articulación universal. El primer uso registrado del término "unión universal" para este dispositivo fue realizado por Hooke en 1676, en su libro Helioscopios.​​​ Publicó una descripción en 1678,​ que dio como resultado el uso del término de junta de "Hooke" en el mundo de habla inglesa. En 1683, Hooke propuso una solución a la velocidad de rotación no uniforme de la junta universal: un par de juntas de Hooke desfasadas 90° en cada extremo de un eje intermedio, una disposición que ahora se conoce como un tipo de junta homocinética.​​ El sueco Christopher Polhem posteriormente reinventó la junta universal, dando lugar al nombre de Polhemsknut (nudo Polhem) en sueco.

En 1841, el científico inglés Robert Willis analizó el movimiento de la articulación universal.​ En 1845, el ingeniero y matemático francés Jean-Victor Poncelet había analizado el movimiento de la articulación universal mediante trigonometría esférica.​

El término "articulación universal" se usó en el siglo XVIII​ y fue de uso común en el siglo XIX. La patente de 1844 de Edmund Morewood de una máquina para tratar piezas de metal requería una junta universal, con el fin de eliminar pequeños errores de alineación entre el motor y los ejes de laminación.​ La patente de la locomotora Shay, de Ephriam Shay de 1881, por ejemplo, usaba juntas universales dobles como eje de transmisión.​ Charles Amidon utilizó una junta universal mucho más pequeña en su berbiquí patentado 1884.​ El motor de vapor esférico, rotativo y de alta velocidad de Beauchamp Tower utilizó una adaptación de la junta universal alrededor de 1885.​

El término "junta de cardán" parece ser un préstamo en el idioma inglés. Muchos usos tempranos en el siglo XIX aparecen en traducciones procedentes del idioma francés o están fuertemente influidos por el uso del francés. Los ejemplos incluyen un informe de 1868 sobre la Exposición Universal de París (1867)​ y un artículo sobre el dinamómetro traducido del francés en 1881.​

Ecuación del movimiento

Diagrama de variables para la junta universal. El eje 1 es perpendicular al plano rojo y el eje 2 es perpendicular al plano azul en todo momento. Estos planos forman un ángulo β el uno con respecto al otro. El desplazamiento angular (posición de rotación) de cada eje viene dado por $\gamma _{1}$ y $\gamma _{2}$ respectivamente, que son los ángulos de los vectores unitarios ${\hat {x}}_{1}$ y ${\hat {x}}_{2}$ con respecto a sus posiciones iniciales en los ejes x e y. Los vectores ${\hat {x}}_{1}$ y ${\hat {x}}_{2}$ están fijados por el cardán que conecta los dos ejes, por lo que están obligados a permanecer perpendiculares entre sí en todo momento.

Velocidad angular del eje de salida (rotacional) $\omega _{2}\,$ frente al ángulo de rotación $\gamma _{1}\,$ para diferentes ángulos de curvatura $\beta \,$ de la junta.

Ángulo de rotación del eje de salida, $\gamma _{2}\,$, frente al ángulo de rotación del eje de entrada, $\gamma _{1}\,$, para diferentes ángulos de curvatura, $\beta \,$, de la articulación.

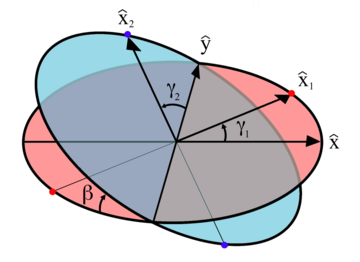
La articulación del cardán sufre un problema importante: incluso cuando el eje del árbol de transmisión de entrada gira a velocidad constante, el eje del árbol de transmisión de salida gira a una velocidad variable, lo que provoca vibración y desgaste. La variación en la velocidad del eje impulsado depende de la configuración de la unión, que se especifica mediante tres variables:

1. $\gamma _{1}$, el ángulo de rotación para el eje 1
2. $\gamma _{2}$, el ángulo de rotación para el eje 2
3. $\beta$, el ángulo de plegado de la junta, o el ángulo de los ejes con respecto a cada uno, con el cero siendo paralelo o recto.

Estas variables se ilustran en el diagrama de la derecha. También se muestra un conjunto de coordenadas cartesianas fijo con vectores unitarios ${\hat {\mathbf {x} }}$ e ${\hat {\mathbf {y} }}$, y los planos de rotación de cada eje. Estos planos de rotación son perpendiculares a los ejes de rotación y no se mueven cuando los ejes giran. Los dos ejes están unidos por un cardán que no se muestra. Sin embargo, el eje 1 se une al cardán en los puntos rojos en el plano de rotación rojo en el diagrama, y el eje 2 se une en los puntos azules en el plano azul. Los sistemas de coordenadas fijos con respecto a los ejes rotativos se definen teniendo sus vectores unitarios del eje x (${\hat {\mathbf {x} }}_{1}$y ${\hat {\mathbf {x} }}_{2}$) apuntando desde el origen hacia uno de los puntos de conexión. Como se muestra en el diagrama, ${\hat {\mathbf {x} }}_{1}$está en el ángulo $\gamma _{1}$con respecto a su posición inicial en el eje x, y ${\hat {\mathbf {x} }}_{2}$ está en el ángulo $\gamma _{2}$con respecto a su posición inicial en el eje y.

${\hat {\mathbf {x} }}_{1}$ está confinado al "plano rojo" en el diagrama y está relacionado con $\gamma _{1}$ por:

${\hat {\mathbf {x} }}_{1}=[\cos \gamma _{1}\,,\,\sin \gamma _{1}\,,\,0]$

${\hat {\mathbf {x} }}_{2}$ está confinado al "plano azul" en el diagrama y es el resultado del vector unitario en el eje x ${\hat {x}}=[1,0,0]$girando a través de los ángulos de Euler $[\pi \!/2\,,\,\beta \,,\,0$]:

${\hat {\mathbf {x} }}_{2}=[-\cos \beta \sin \gamma _{2}\,,\,\cos \gamma _{2}\,,\,\sin \beta \sin \gamma _{2}]$

Una restricción en los vectores ${\hat {\mathbf {x} }}_{1}$ y ${\hat {\mathbf {x} }}_{2}$ es que, como están fijados en la suspensión cardán, deben permanecer en ángulos rectos entre ellos. Esto es así cuando su producto escalar es igual a cero:

${\hat {\mathbf {x} }}_{1}\cdot {\hat {\mathbf {x} }}_{2}=0$

Por lo tanto, la ecuación de movimiento que relaciona las dos posiciones angulares viene dada por:

$\tan \gamma _{1}=\cos \beta \tan \gamma _{2}\,$

con una solución formal para $\gamma _{2}$:

$\gamma _{2}=\tan ^{-1}[\tan \gamma _{1}/\cos \beta ]\,$

La solución para $\gamma _{2}$no es única, ya que la función arco tangente admite múltiples raíces; sin embargo, se requiere que la solución para $\gamma _{2}$sea continua en los ángulos analizados. Por ejemplo, la siguiente solución explícita que utiliza la función atan2 (y, x) será válida para $-\pi <\gamma _{1}<\pi$:

$\gamma _{2}=\mathrm {atan2} (\sin \gamma _{1},\cos \beta \,\cos \gamma _{1})$

Los ángulos $\gamma _{1}$y $\gamma _{2}$en una articulación rotativa serán función del tiempo. La diferenciación de la ecuación de movimiento con respecto al tiempo y el uso de la ecuación de movimiento en sí para eliminar una variable produce la relación entre las velocidades angulares $\omega _{1}=d\gamma _{1}/dt$ y $\omega _{2}=d\gamma _{2}/dt$:

$\omega _{2}={\frac {\omega _{1}\cos \beta }{1-\sin ^{2}\beta \cos ^{2}\gamma _{1}}}$

Como se muestra en las gráficas, las velocidades angulares no están relacionadas linealmente, sino que son periódicas, con un período de la mitad del de los ejes giratorios. La ecuación de velocidad angular se puede diferenciar nuevamente para obtener la relación entre las aceleraciones angulares $a_{1}$y $a_{2}$:

$a_{2}={\frac {a_{1}\cos \beta }{1-\sin ^{2}\beta \,\cos ^{2}\gamma _{1}}}-{\frac {\omega _{1}^{2}\cos \beta \sin ^{2}\beta \sin 2\gamma _{1}}{(1-\sin ^{2}\beta \cos ^{2}\gamma _{1})^{2}}}$

Como se puede apreciar en la gráfica de la derecha, cuanto mayor es el ángulo que forman los dos ejes, mayores son las diferencias tanto de velocidad como de aceleración angular entre ambos.

Funcionamiento

Junta cardán en movimiento.

Las juntas cardánicas son mecanismos simples y robustos. Están constituidas por dos piezas en forma de horquilla -las horquillas- conectadas entre sí por medio de otra pieza en forma de cruz -la cruceta-. Los cuatro extremos de la cruceta están montados sobre cojinetes encajados a presión en unos alojamientos en las horquillas y sujetos mediante bridas. El movimiento del eje conductor se transmite a través de la cruceta al eje conducido, permitiendo diferencias angulares de hasta 25 grados.​

Usos en la industria automotriz

En la actualidad el uso principal de las juntas cardánicas está en el árbol de transmisión, que lleva la fuerza desde el motor situado en la parte delantera del vehículo hacia las ruedas traseras de los vehículos de tracción trasera, habiendo dejado prácticamente de utilizarse en semiejes por sus desventajas frente a las juntas homocinéticas.

Actualmente la práctica totalidad de los automóviles de turismo de tracción trasera utilizan suspensiones independientes o excepcionalmente eje De Dion. En ambos casos el diferencial está fijado al chasis, por lo que el árbol no está sujeto a requerimientos de grandes desplazamientos angulares ni de variaciones de longitud.

Los árboles en estas transmisiones suelen utilizar juntas cardánicas para asumir los desplazamientos del motor y del diferencial sobre sus silentblocks. En estos sistemas suele emplearse un eje dividido en dos tramos para reducir el volumen del túnel de transmisión, siempre con dos juntas cardánicas, generalmente en el segundo tronco, y un flector a la salida de la caja de cambios para proporcionar un ligero efecto telescópico y absorber vibraciones.

Un uso secundario muy extendido está en las columnas de dirección colapsables.​

Utilización histórica

Árbol de transmisión Hotchkiss con junta deslizante y dos juntas cardánicas.

Este vídeo muestra las diferentes partes y la operación de un eje cardán.

• Árboles de transmisión:

Las transmisiones Hotchkiss, hoy solo empleadas en vehículos todo-terreno e industriales, utilizan un tipo especial de árbol de transmisión. En este sistema el árbol está sometido a unos requerimientos cinemáticos muy elevados, puesto que debe seguir el movimiento del diferencial integrado en el puente trasero a lo largo del recorrido de la suspensión. Por esta razón estos árboles necesitan juntas muy robustas, que permitan grandes desplazamientos angulares y a la vez se adapten a las variaciones de longitud generadas por el movimiento del puente. La solución vino de la mano del empleo de árboles con dos juntas cardánicas —universal shafts—, una a cada extremo y una junta deslizante intermedia. En este caso una de las horquillas va unida al tubo de la transmisión y la otra lleva la brida de acoplamiento para su unión al grupo propulsor del puente. En el otro lado del tubo, la junta cardán va montada sobre una unión deslizante, formada por un manguito estriado interiormente que forma parte de una de las horquillas, acoplándose al estriado del tubo. El conjunto así formado constituye una unión oscilante y deslizante.​

Por el contrario, las transmisiones por tubo de empuje utilizaban un árbol cubierto por un tubo de empuje en prolongación del cárter del diferencial. El árbol de transmisión de estas transmisiones utilizaba una única junta cardánica a la salida de la caja de cambios, cubierta por una rótula a través de la que se transmitía el empuje a la caja de cambios y de ahí al chasis a través de los anclajes del motor.

• Semiejes:

Los semiejes que conectan el diferencial con las ruedas en los vehículos con suspensión independiente montaron originariamente juntas cardánicas, bien a la salida del diferencial (ejes oscilantes), bien en ambos extremos junto con un mecanismo telescópico en el resto de los sistemas.

Sin embargo, cuando se utilizaron en los primeros vehículos de tracción delantera, las juntas cardánicas se enfrentaron a su característica irregularidad periódica; como dicha irregularidad aumenta con el ángulo formado por los árboles, al ángulo entre el semieje y la rueda se suma el ángulo de giro de la rueda, que puede ser tan elevado que genere una vibración que afecte a semiejes y caja de cambios.

Una primera solución fue emplear un árbol de transmisión con una junta cardánica a la salida de la caja de cambios, junto con una junta delizante y un doble cardán en el lado de la rueda, sistema empleado en los primeros Citroën o BMC de tracción delantera. Estas primeras transmisiones pronto fueron sustituIdas por el sistema actual de juntas homocinéticas con la universalización de la disposición Giacosa.​

Otra alternativa empleada en los primeros vehículos todo terreno fue asumir la irregularidad, empleando un eje con solo dos juntas cardánicas reforzadas, donde la falta de adherencia permitía el resbalamiento de la rueda sin afectar a la transmisión.

Véase también

• Eje de transmisión
• Junta homocinética

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre juntas cardán.
• Animación en 3D de una cardán telescópica doble (homocinética).

• Datos: Q862003
• Multimedia: Universal joints / Q862003