Oscilador armónico
Se dice que un sistema cualquiera, mecánico, eléctrico, neumático, etc., es un oscilador armónico si, cuando se deja en libertad fuera de su posición de equilibrio, vuelve hacia ella describiendo oscilaciones sinusoidales, o sinusoidales amortiguadas en torno a dicha posición estable.

El ejemplo es el de una masa colgada a un resorte. Cuando se aleja la masa de su posición de reposo, el resorte ejerce sobre la masa una fuerza que es proporcional al desequilibrio (distancia a la posición de reposo) y que está dirigida hacia la posición de equilibrio. Si se suelta la masa, la fuerza del resorte acelera la masa hacia la posición de equilibrio. A medida que la masa se acerca a la posición de equilibrio y que aumenta su velocidad, la energía potencial elástica del resorte se transforma en energía cinética de la masa. Cuando la masa llega a su posición de equilibrio, la fuerza será cero, pero como la masa está en movimiento, continuará y pasará del otro lado. La fuerza se invierte y comienza a frenar la masa. La energía cinética de la masa va transformándose ahora en energía potencial del resorte hasta que la masa se para. Entonces este proceso vuelve a producirse en dirección opuesta completando una oscilación.
Si toda la energía cinética se transformase en energía potencial y viceversa, la oscilación seguiría eternamente con la misma amplitud. En la realidad, siempre hay una parte de la energía que se transforma en otra forma, debido a la viscosidad del aire o porque el resorte no es perfectamente elástico. Así pues, la amplitud del movimiento disminuirá más o menos lentamente con el paso del tiempo. Se empezará tratando el caso ideal, en el cual no hay pérdidas. Se analizará el caso unidimensional de un único oscilador (para la situación con varios osciladores, véase movimiento armónico complejo).
Casos[editar]
Oscilador armónico sin pérdidas[editar]
Se denominará a la distancia entre la posición de equilibrio y la masa, a la que se le dominara . Se supondrá que la fuerza del resorte es estrictamente proporcional al desequilibrio: (ley de Hooke). es la fuerza y la constante elástica del resorte. El signo negativo indica que cuando es positiva la fuerza está dirigida hacia las negativas.
La segunda ley de Newton nos dice:
remplazando la fuerza obtenemos:
La solución de esta ecuación diferencial ordinaria es inmediata: las únicas funciones reales (no complejas) cuya segunda derivada es la misma función con el signo invertido son seno y coseno. Las dos funciones corresponden al mismo movimiento. Escogemos arbitrariamente "coseno". La solución se escribe:

| Símbolo | Nombre |
|---|---|
| Elongación o diferencia respecto al estado de equilibrio | |
| Amplitud, máxima diferencia respecto a la posición de equilibrio | |
| Pulsación (o frecuencia angular) | |
| Frecuencia | |
| Tiempo | |
| Fase inicial (para ) |
Es fácil comprobar que el valor de es: El período de oscilación es: Como ya hemos dicho, durante un cuarto de una oscilación la energía potencial se transforma en energía cinética. Durante otro cuarto, la energía cinética se transforma en energía potencial. En la figura de la derecha se ha trazado la posición en función del tiempo (curva de arriba), la velocidad en función del tiempo (en medio) y las energías potenciales y cinéticas (abajo).
Oscilador armónico amortiguado[editar]

Es el caso de rozamientos secos: la fuerza no depende ni de la velocidad ni de la posición. Otra situación que se produce en la realidad es que la fuerza sea proporcional a la velocidad elevada a una potencia, entera o no. Así sucede cuando la fuerza que frena proviene de la viscosidad o de las pérdidas aerodinámicas. Se tratará únicamente el caso más simple, es decir, cuando la fuerza sea proporcional a la velocidad. En este caso la fuerza será:
Donde es un coeficiente que mide el amortiguamiento debido a la viscosidad. Si es pequeño, el sistema está poco amortiguado. Nótese el signo negativo que indica, como antes, que si la velocidad es positiva, la fuerza tiene la dirección superior opuesta a la velocidad de la partícula. Con este término complementario la ecuación diferencial del sistema es:
Se trata de una ecuación diferencial ordinaria, lineal, de segundo orden[1] (contiene derivadas segundas) y homogénea (no hay término independiente de ). Tiene tres tipos de soluciones según el valor de :
- Si el sistema está sobreamortiguado (amortiguamiento fuerte o supercrítico)
- Si el sistema tiene amortiguamiento crítico.
- Si el sistema oscila con amplitud decreciente (amortiguamiento débil o subcrítico)
Oscilador sobreamortiguado[editar]
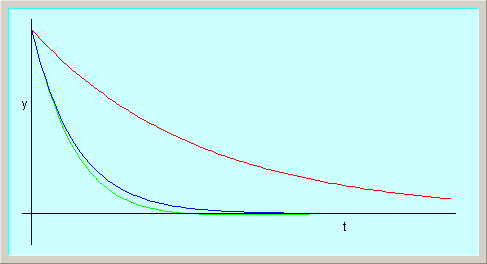
| curva azul: amortiguamiento crítico. |
| curva roja: amortiguamiento doble que el crítico. |
| curva verde: amortiguamiento igual a 90% del amortiguamiento crítico. |
En este caso el sistema no es realmente un oscilador, ya que no oscila. La solución es de la forma:
donde los coeficientes de las exponenciales son menores que cero y reales (por lo que no hay oscilación):
y
y dependen de las condiciones iniciales (es decir, de la situación del sistema para ). La posición no es oscilante y tiende hacia la posición de equilibrio de manera asintótica. Las dos exponenciales decrecientes de las soluciones tienen constantes de tiempo diferentes. Una es pequeña y corresponde a la rápida cancelación del efecto de la velocidad inicial. La segunda es más grande y describe la lenta tendencia hacia la posición de equilibrio.
Oscilador con amortiguamiento crítico[editar]
Este caso es el límite entre un sistema oscilante y uno no oscilante. Ocurre cuando
La solución única es:
como antes, y son constantes que dependen de las condiciones iniciales.
El amortiguamiento crítico corresponde a la tendencia más rápida hacia la situación de equilibrio cuando no sobrepasa esa posición. Si se disminuye un poco el amortiguamiento el sistema se acerca más rápidamente a la posición de equilibrio, pero sobrepasando la posición oscila en torno a ese punto (tomando valores positivos y negativos).
Oscilador con amortiguamiento débil[editar]

En este caso, que es más interesante, tenemos un oscilador que oscila alrededor de la posición de equilibrio con amplitud decreciente. Sucede cuando:
La solución es:
como antes, y son constantes que dependen de las condiciones iniciales. La pulsación es:
La pulsación del sistema amortiguado es un poco menor que la pulsación del sistema no amortiguado porque la fuerza que lo amortigua, frena la masa y la retarda.
La oscilación del sistema está descrita por una sinusoide de frecuencia cuya amplitud está multiplicada por una exponencial decreciente cuya constante de tiempo es .
Factor de calidad Q[editar]
En un sistema poco amortiguado es conveniente definir el factor de calidad' (Quality factor en inglés), denotado por Q, como:
Esta cantidad es igual a veces el inverso de las pérdidas relativas de energía por período. Así, un sistema que pierde 1% de energía a cada ciclo, tendrá un Q de 628. Más interesante, Q es también veces el número de oscilaciones que el sistema hace mientras su amplitud decrece por un factor . Aceptando una aproximación más burda, Q es 3 veces el número de oscilaciones que un sistema hace mientras su amplitud cae a 1/3 de la amplitud inicial.
Como ejemplos, el Q de un vehículo con los amortiguadores en buen estado es algo mayor que 1. El Q de una cuerda de guitarra es de varios miles. El Q de los cristales de cuarzo utilizados en electrónica como referencia de frecuencia es del orden de 1 millón. Una copa de vidrio ordinario tiene un Q mucho más pequeño que una copa de vidrio de plomo (cristal).
Oscilaciones forzadas[editar]
Podemos iniciar el movimiento un oscilador armónico desplazándolo de su posición de equilibrio y abandonándolo a su oscilación libre (ver párrafos precedentes).
Alternativamente, podemos aplicarle una fuerza cuya intensidad varíe de manera sinusoidal con el tiempo. En esta situación, la ecuación diferencial lineal no es homogénea. La solución a este tipo de ecuación consta de dos términos: la solución general del sistema homogéneo más una solución particular del caso inhomogéneo.[2] Por tanto, la solución tiene dos partes: una parte transitoria (que se anula pasado cierto tiempo), similar a las que vimos en los párrafos precedentes, y una parte estacionaria. La solución de la parte transitoria es la misma la que ya hemos visto (ecuación homogénea). Las únicas diferencias son las condiciones iniciales y finales, que no son idénticas. Vamos a interesarnos por la solución estacionaria. En la ecuación diferencial del sistema hay que añadir la fuerza sinusoidal:
Para resolver esta ecuación utilizaremos el mismo método que en electricidad y electrónica. Para ello, se añade a la fuerza real una fuerza imaginaria . Como en electrónica, se utiliza la notación en lugar de i. Ahora la ecuación a resolver es:
Pero por supuesto, como en electricidad, sólo la parte real de será de interés. La solución es inmediata:
Si se deriva esta expresión y se sustituye en la ecuación diferencial, se encuentra el valor de A:
Pero A puede escribirse como y la solución de compleja es:
El valor de real es la parte real de la expresión precedente:
donde es el módulo de y su argumento:
Como en electricidad, el ángulo da el desfase del movimiento con respecto a la fuerza externa. Si es positivo, el movimiento tiene la fase adelantada y si es negativo el movimiento tiene la fase retrasada. En este caso el desfase será siempre negativo.
Respuesta en frecuencia[editar]
La amplitud de las oscilaciones forzadas dependerá, por supuesto, de la amplitud de la fuerza externa. Pero para una misma amplitud de la fuerza, la amplitud de la oscilación dependerá también de la frecuencia. Veamos como varía la amplitud con . Utilizando la definición de frecuencia propia del sistema (sin amortiguamiento ni fuerza externa):

se puede escribir:
Si además se utiliza la definición de , se obtiene:
En el dibujo de derecha se ha representado la amplitud de la oscilación forzada en función de la frecuencia para varios valores del factor de calidad Q. A muy baja frecuencia la amplitud es la misma que si la fuerza fuese estática , y el sistema oscilará entre las posiciones y . Cuando la frecuencia aumenta, la amplitud también, alcanzando un máximo cuando la frecuencia de excitación es igual a la frecuencia propia del sistema. A esa frecuencia propia también se le llama frecuencia de resonancia. También se dice que un sistema excitado a una frecuencia próxima a la frecuencia de resonancia "resuena" o "entra en resonancia". A la frecuencia de resonancia, la amplitud de las oscilaciones será Q veces más grande que la que se obtiene en baja frecuencia.
El ancho del pico de resonancia a media altura, es decir cuando la amplitud es igual a la mitad del máximo, es igual a la frecuencia de resonancia dividida por Q. Ese ancho también se llama banda pasante.
Oscilador forzado y caos[editar]
El oscilador armónico no perturbado en una dimensión es un ejemplo de sistema integrable, con comportamiento regular. Sin embargo, el oscilador armónico perturbado puede presentar un comportamiento caótico[3] caracterizado por un atractor extraño. Por ejemplo en el caso de una perturbación de tipo la ecuación de movimiento es:
Este sistema es no integrable y el movimiento tiende rápidamente hacia el llamado atractor de Duffing.[4]
Oscilador de van der Pol[editar]

El oscilador de van der Pol es un caso especial de oscilador con amortiguamiento no lineal, que responde a la ecuación:
Fue descrito por primera vez en 1935 por Balthasar van der Pol[5] y presenta comportamiento caótico.
Oscilador armónico torsional[editar]
Importancia en física[editar]
Considérese el caso de un cuerpo sometido a una fuerza unidimensional: . Desarrollando dicha fuerza en serie de Taylor alrededor del punto de equilibrio ():
Como el origen es el punto de equilibrio, el primer término del desarrollo es nulo. Si las oscilaciones en torno a son lo suficientemente pequeñas, uno se puede quedar con la aproximación lineal y despreciar los términos de orden superior:
Llamándole a la derivada de la fuerza, se obtiene de nuevo la fuerza recuperadora de Hooke. Aquí radica la importancia del oscilador armónico: supone una primera aproximación para el estudio de un sistema cuando se producen pequeñas oscilaciones en torno a su posición (o estado) de equilibrio.[6]
Ejemplos[editar]
Circuito LC[editar]
Circuito LC sin pérdidas[editar]

En la figura de la derecha se ha dibujado un circuito oscilante LC (una bobina y un condensador) ideal, es decir sin pérdidas.
Supóngase que, en la situación inicial, el condensador está cargado a una tensión V y que en ese momento se conecta la inductancia. La tensión presente en las extremidades de la inductancia va a hacer aparecer una corriente de sentido inverso a la de la flecha del dibujo, que aumentará con el tiempo. A medida que el condensador suministra corriente a la inductancia, se descarga y la tensión disminuye. La disminución de la tensión hace que la corriente aumente menos rápidamente. La situación continúa así, con la tensión del condensador que disminuye cada vez más rápidamente (porque la corriente aumenta) y la corriente que aumenta más lentamente (porque la tensión disminuye). Llega un momento en el cual el condensador está completamente descargado y la corriente ha llegado a un máximo.
Ahora la corriente continúa circulando porque la inductancia se lo impone. El condensador comienza a cargarse en el otro sentido y hace aparecer una tensión en los bornes de la inductancia que hace disminuir la corriente. La situación continúa del siguiente modo: el condensador se va cargando cada vez más lentamente (porque la corriente disminuye), mientras que la corriente va disminuyendo cada vez más rápidamente (porque la tensión inversa aumenta). Así, se llega a la situación en la cual la corriente se anula y la tensión del condensador es máxima y del mismo valor que la tensión inicial, pero con sentido opuesto. La situación es análoga a la de una masa sostenida por un resorte. La inductancia juega el papel de la masa. La masa tiene inercia e impide que el movimiento cambie bruscamente. La inductancia impide que la corriente cambie bruscamente. Veamos las ecuaciones.
El comportamiento eléctrico del condensador está descrito por la ecuación: . El de la inductancia está descrito por . Como en el esquema es positivo cuando sale del lado positivo de la inductancia, hay que agregar un signo negativo: . Se tiene, pues, este sistema de ecuaciones diferenciales:
Para eliminar , basta derivar la primera ecuación, para reemplazar la derivada de en la segunda:
que se puede escribir como:
Esta ecuación es la misma que la de la masa con un resorte. es equivalente a la posición . es equivalente a la masa y es equivalente a la constante del resorte .
La solución es:
con
Como de costumbre, y dependen de las condiciones iniciales.
Circuito LC con pérdidas[editar]
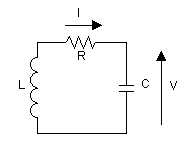
El esquema de la derecha representa un circuito oscilante LC con pérdidas. Las pérdidas están representadas por las pérdidas en una resistencia. En un circuito real, las pérdidas provienen de resistencias en serie como la dibujada. Dichas resistencias pueden estar en el exterior de la inductancia o del condensador, pero también pueden ser resistencias internas de esos componentes. También puede haber resistencias en paralelo, perdidas en el dieléctrico del condensador o en el núcleo de la bobina (si es ferromagnético). También puede haber pérdidas por radiación de ondas electromagnéticas. La resistencia hará que la tensión sobre la bobina sea diferente de la tensión sobre el condensador. La corriente creada será menor que si no hubiese habido pérdidas y cuando la corriente cargue de nuevo el condensador, la tensión a la cual llegará será menor. Por su parte, la amplitud disminuirá y tenderá hacia cero. La ecuación del nuevo sistema es:
La ecuación es la misma que la de una masa con un resorte y con un amortiguador. Esta vez es el equivalente del coeficiente de rozamiento . La solución es:
con
y
donde es la frecuencia propia del circuito (sin pérdidas).
Oscilaciones forzadas de un circuito LC con pérdidas[editar]
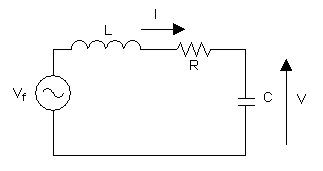
El esquema de la derecha muestra un generador conectado a un circuito LC en serie. Si la tensión del generador es , la ecuación es:
La expresión se puede reescribir, dándole un aspecto similar a las formas precedentes:
Como en el ejemplo mecánico, en régimen estacionario la solución es:
donde
y
y son los mismos que en el párrafo precedente. La amplitud de la tensión de salida es máxima a la resonancia (cuando ) y vale veces la tensión de entrada.
Oscilador armónico cuántico[editar]


Susodichamente, el oscilador armónico se puede emplear para estudiar sistemas que realicen pequeñas oscilaciones en torno a una posición de equilibrio. En particular, el oscilador armónico cuántico se puede emplear para estudiar las oscilaciones de los átomos de una molécula diatómica, como la de hidrógeno, H2, o la de cloruro de hidrógeno, HCl.[7]
El oscilador armónico es uno de los casos en los que se puede obtener una solución analítica sencilla de la ecuación de Schrödinger. En esta situación, el hamiltoniano de la partícula considerada estará descrito por:
Nótese que para el caso de moléculas diatómicas, la masa sería, en realidad, la masa reducida del sistema. Se ve claramente que el primer sumando es un término cinético, mientras que el segundo es el armónico. Como el hamiltoniano no depende del tiempo, sólo resta resolver la ecuación de Schrödinger independiente del tiempo, a fin de hallar los autoestados de la energía :
Se puede demostrar que las funciones de onda, , cuyo módulo al cuadrado describe la densidad de probabilidad de que la partícula tenga una determinada posición , son el producto de exponenciales por los polinomios de Hermite. La figura de la derecha muestra la forma de dichas funciones para los seis autoestados con energía más baja (el estado de menor energía es el que figura en la parte superior de la misma). En particular, la energía del nivel n-ésimo será:
donde es la constante de Planck.
Es importante señalar un par de hechos:
- Los niveles de energía se encuentran cuantizados, es decir, sólo pueden tomar una serie de valores discretos.
- El nivel mínimo de energía no es cero, sino . Nótese que la función de onda de dicho estado muestra que la partícula no se encuentra en todo momento en la posición de equilibrio .
En la segunda figura, se muestran las densidades de probabilidad espacial de la partícula para los diferentes autoestados. Nótese que a medida que crece la energía del autoestado considerado (es decir, el orden ), las distribuciones de probabilidad tienden a concentrarse en los puntos de retorno, o máxima amplitud. Esta situación es la que se da en el caso clásico, si se define para él una densidad de probabilidad inversamente proporcional a la velocidad de la partícula en cada punto.[8] Por tanto, se cumple el principio de correspondencia (es decir, se pueden predecir los resultados que se obtendrían en el límite clásico).
Véase también[editar]
- Péndulo
- Péndulo cicloidal
- Péndulo de Newton
- Péndulo de Pohl
- Péndulo de torsión
- Péndulo físico
- Péndulo simple
Referencias[editar]
- ↑ Simmons, capítulo 3
- ↑ Simmons, páginas 84-87
- ↑ T.N. Palmer (1995): "A local deterministic model of Quantum Spin Measurement", Proceedings: Mathematical and Physical Sciences, Volume 451, Issue 1943, pp. 585-608
- ↑ Atractor de Duffing
- ↑ Cartwright, M.L., "Balthazar van der Pol", J. London Math. Soc., 35, 367-376, (1960).
- ↑ Marion, páginas 103 y 104
- ↑ Tipler, página 1190
- ↑ Guillén, páginas 114 y 115
Bibliografía[editar]
- Feynman, Leighton and Sands (1964). Lectures on physics. Addison-Wesley. ISBN 0-8053-9045-6.
- R. Resnick and D. Halliday (1996). Physics. John Wiley & Sons. ISBN 0-471-83202-2.
- Marion, Jerry B. (1996). Dinámica clásica de las partículas y sistemas. Barcelona: Ed. Reverté. ISBN 84-291-4094-8.
- Simmons, George F. (1999). Ecuaciones Diferenciales. Con aplicaciones y notas históricas. Aravaca (Madrid): McGraw-Hill. ISBN 84-481-0045-X.
- Tipler, Paul A. (2000). Física para la ciencia y la tecnología (volumen 2). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.
- Sánchez Guillén, Joaquín. Braun, Mijail A. (1993). Física cuántica. Madrid: Alianza Editorial. ISBN 84-206-8145-8.
Enlaces externos[editar]
- Artículo en la Wikipedia en francés sobre el péndulo compuesto
- Hyperphysics (sitio en inglés)
- Oscilador armónico cuántico en Hyperphysics.
- Página (en inglés) con animaciones acerca del oscilador armónico, el péndulo simple y otros fenómenos.
- Página Archivado el 20 de junio de 2018 en Wayback Machine. (en inglés) con animaciones de oscilaciones y ondas.














































































































