Circuito LC

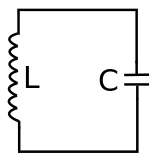
Un Circuito LC, también denominado circuito resonante u oscilador LC, es un circuito eléctrico formado por una bobina, representado por la letra L y un condensador, representado por la letra C, los cuales se encuentran conectados entre sí. El circuito actúa como un resonador eléctrico, como una analogía eléctrica a un diapasón, basado en el almacenamiento de energía oscilante a la frecuencia de resonancia del circuito.

Los circuitos LC se usan para generar señales a una frecuencia específica, o para seleccionar una señal de una frecuencia específica de una señal más compleja; está función se denomina filtro paso banda. Son componentes fundamentales en muchos dispositivos electrónicos, particularmente en equipos de radio, donde son usados en circuitos como osciladores, filtros, sintonizadores y mezcladores de frecuencias.

Un circuito LC es un modelo idealizado, ya que se asume que no hay disipación de energía debido a que no hay resistencia eléctrica. Cualquier implementación práctica de un LC siempre tendrá pérdidas debido a una pequeña resistencia (que no es igual a cero), entre los componentes y los cables de conexión. A pesar de que los circuitos en la vida real tendrán pérdidas, es importante estudiar este modelo de circuito para entender el fenómeno y tener intuición física. Para un modelo de circuito que incluye resistencia, por favor ver el circuito RLC.

Análisis[editar]

En un circuito resonante, la impedancia total vendrá dada por:

$Z={\sqrt {R^{2}+(X_{L}-X_{C})^{2}}}\,\!$ y siendo, $X_{L}=X_{C}\,\!$ , entonces $Z={\sqrt {R^{2}}}\,\!$ , y así $Z=R\,\!$

Donde Z es la impedancia, que se podría definir como la resistencia en circuitos de corriente alterna. En el estado de resonancia eléctrica, al ser la impedancia mínima, la intensidad eficaz de la corriente será máxima. Simultáneamente, la diferencia de potencial o tensión eléctrica correspondiente a $X_{C}\,\!$ y $X_{L}\,\!$ , tiene valores máximos iguales.

Funcionamiento del circuito[editar]

Al estar el condensador y la bobina en paralelo, la energía almacenada por el campo eléctrico del condensador (en forma de cargas electrostáticas), es absorbida por la bobina, que la almacena en su campo magnético, pero a continuación es absorbida y almacenada por el condensador; nuevamente en forma de campo eléctrico; para ser nuevamente absorbida por la bobina, y así sucesivamente. Esto crea un vaivén de la corriente (cargas eléctricas) entre el condensador y la bobina. Este vaivén constituye una oscilación electromagnética, en la cual el campo eléctrico y el magnético son perpendiculares entre sí, que cuando el campo magnético de la bobina está en su punto máximo, el campo eléctrico almacenado en el condensador es cero, y que cuando el campo eléctrico en el condensador es máximo, no existe campo magnético en la bobina.

El campo magnético sólo existe cuando los electrones están en movimiento, partiendo desde la placa negativa del condensador, hacia la placa positiva, a través de la bobina. Una vez que se ha movido una cierta cantidad de electrones, haciendo que haya la misma cantidad de electrones en ambas placas, logrando así el equilibrio; en este momento se reduce a 0 voltios la diferencia de potencial en el condensador (y en la bobina, al estar esta conectada en serie). En este momento al cesar el movimiento de los electrones, se detiene entonces la producción del campo magnético en la bobina, por lo que el campo magnético previamente producido por dicha bobina, colapsa sobre ella, produciendo una auto-inducción de voltaje con polaridad opuesta.

En ese momento el voltaje auto-inducido por la bobina crea una fuerza electromotriz que provoca el movimiento de los electrones, desde la placa que antes era la positiva (la que carecía de electrones, que luego se equilibró), hacia la que antes era la negativa (la que tenía electrones en excedencia, que luego los cedió y logró su equilibrio). De esta forma la bobina carga al condensador con polaridad opuesta, hasta que esta haya agotado y consumido por completo su campo magnético. A partir de aquí, se repite el ciclo nuevamente.

Cabe aclarar que en cada ciclo o vaivén de carga y descarga, hay pérdidas debido a la resistencia eléctrica del conductor que conforma la bobina, y a las fugas del dieléctrico que conforma al condensador. Por lo que en cada ciclo, el voltaje al que se carga el condensador irá siendo menor, hasta agotarse con el tiempo. Es por eso que se necesitan circuitos electrónicos amplificadores, que reponen el voltaje perdido, para mantener las oscilaciones constantes y por tiempo indefinido.

Otra característica de los circuitos resonantes es que la energía liberada por un elemento reactivo (inductor o condensador) es exactamente igual a la absorbida por el otro. Es decir, durante la primera mitad de un ciclo de entrada el inductor absorbe toda la energía liberada por el condensador, y durante la segunda mitad del ciclo el condensador vuelve a capturar la energía proveniente del inductor. Es precisamente esta condición "oscilatoria" la que se conoce como resonancia, y la frecuencia en la que esta condición se da es llamada frecuencia resonante.

Los circuitos resonantes son especialmente útiles cuando se desea hacer "sintonizadores" (conocidos en el inglés como "tuners"), en los que se quiere dar suficiente potencia a solamente una frecuencia (o un rango de frecuencias muy reducido) dentro de un espectro. Por ejemplo, cuando sintonizamos una emisora de radio en nuestro receptor lo que se ha producido es una condición de resonancia para la frecuencia central asignada para dicha estación radiodifusora. En el caso de los receptores de radio comerciales tienen un circuito resonante "ajustable" para poder seleccionar la frecuencia resonante adecuada. En las emisoras de FM, los rangos de frecuencia varían entre 88 y 108 MHz, mientras que en la AM los rangos de frecuencia de Onda Media oscilan entre 535 y 1705 kHz.

Frecuencia de la oscilación[editar]

La característica de este tipo de circuito, es que la velocidad con que fluye y regresa la corriente desde el condensador a la bobina o viceversa, se produce con una frecuencia (f) propia, denominada frecuencia de resonancia, que depende de los valores del condensador (C) y de la bobina (L), y viene dada por la siguiente fórmula de Thomson:

$f={\frac {1}{2\cdot \pi {\sqrt {L\cdot C}}}}$

donde:

f se mide en hercios, C en faradios y L en henrios.

Variable ω[editar]

La variable $\omega$ es equivalente al producto de la frecuencia (f) por el ciclo completo en radianes (2 · $\pi$ ).

$\omega =2\pi f\,$

Este efecto se logra debido a que toda la energía potencial (U) almacenada en el condensador

${\textstyle U={\frac {1}{2}}({\frac {Q^{2}}{C}})={\frac {1}{2}}(C*V^{2})}$ ,

producida por el campo eléctrico en dicho elemento, se traspasa a la bobina la cual, acto seguido, adquiere esta energía y la almacena; es decir, cumple con un sistema conservativo de energía. Este circuito oscilador conocido como tanque LC (en inglés, LC tandem) cumple, asumiendo unos valores de L y C ideales (es decir, suponiendo una inductancia y capacitancia ideales), con la ley de la conservación de la energía (ver conservación de la energía).

Usos[editar]

Los circuitos resonantes o sintonizados tienen un amplio uso:

Radiocomunicación, tanto de radio como de TV: El oscilador de la emisora y del receptor están sintonizados a la misma frecuencia.

Trampa de ondas, tanto de radio como de TV y otras aplicaciones: Una TRAMPA DE ONDAS, (también llamado circuito atrapa ondas), se puede definir como un circuito que contiene al menos un condensador y una inductancia, conectados en serie o en paralelo, para formar un circuito sintonizado. Una forma más común de trampa de onda es la que utiliza un circuito sintonizado en paralelo. Cuando se utiliza un circuito sintonizado en serie se conoce como trampa de onda tipo derivación y funciona de manera opuesta a la trampa de ondas de circuito sintonizado en paralelo. Referencia: "Trampas de ondas", SW Amos, Wireless World, febrero de 1945.

Telecontrol o mando a distancia: La señal oscilante del canal emisor está sintonizada con el del receptor el cual actúa con un circuito conmutador para gobernar artefactos (no confundir con otros mando a distancia basados en señales procesadas digitalmente infrarrojo u otra). Por ejemplo, radiocontrol de modelos aéreos.

Reconocimiento de especies seriadas y autentificación: Es uno de los usos de estos circuitos que suelen pasar inadvertidos para las personas que están en contacto con ellos. Por ejemplo, existen sistemas de validación de acceso basados en tarjetas de identidad que, por su aspecto, no se diferencian de una tarjeta corriente, sin embargo, debajo de su doble capa tiene un circuito oscilador constituido por un gran solenoide de alambre de cobre muy fino y un condensador, ambos sintonizados para oscilar a una frecuencia única: el oscilador de la tarjeta de cada usuario diferente, es capaz de oscilar a una frecuencia diferente. En el sitio de control y validación de acceso, la tarjeta es acercada a una distancia suficiente para entrar en el campo magnético que está siendo generado, permanentemente, por el aparato fijo (escáner o interrogador). El solenoide dentro de la tarjeta en movimiento corta las líneas del campo magnético e induce una corriente que pasa al condensador, el cual es cargado y vuelto a descargar tal como se ha explicado antes. Ese proceso, a su vez, genera una débil onda de radio, a su frecuencia, que es captada dentro del aparato fijo por un circuito oscilador de igual característica que el de la tarjeta. El resultado es que el sistema es capaz de diferenciar cientos de diferentes tarjetas. Si a cada una de ellas, mediante otros recursos técnicos, se les asigna un ítem específico, o código, es posible diferenciar personas y producciones seriadas jugando una función algo similar al reconocimiento a distancia de los códigos de barras. Algunas personas afirman que estas tarjetas tienen un Chip inteligente cuando realmente es un circuito analógico. En aplicaciones más complejas sí pueden contener otros elementos, chip alimentado por la corriente inducida. Como se comprende, estas tarjetas no usan batería; la energía es inducida por el campo magnético externo. Algunos tipos de tarjetas de crédito pueden contener circuitos de esta naturaleza.

Seguridad anti-hurto: Se utiliza en los mercados y se pueden ver adheridas a los diferentes productos en venta. Cuando el objeto atraviesa el campo magnético que genera permanentemente el aparato (escáner) existente en la puerta de salida, el circuito oscilador da salida a una señal que, al ser captada, activa la alarma. Es muy similar a lo ya descrito, solo que, en lugar de la tarjeta con un circuito rígido, se tiene uno impreso sobre material flexible y adherente o pegatina, normalmente papel aluminio en el que se han calado finas venas en espiral que funcionan como solenoide. Las diferentes camadas del papel aluminio, separadas por un dieléctrico, constituyen el condensador. Este ingenioso circuito es suficiente que oscile a una única frecuencia para todos los productos. Estas tarjetas son sometidas a la acción de otro artefacto, en el momento de pagar la factura, encargado de destruirlo internamente aniquilando su capacidad de resonancia por lo que es posible que pase la puerta sin activar la alarma. Las llaves de automóviles modernos, desde 1995, han incorporado un transponder pasivo que incorpora un circuito resonante, a veces contenido en una cápsula de vidrio donde es fácil identificar el solenoide de alambre de cobre.

Multiplexión en comunicaciones: A través de un único par de conductores físicos es posible establecer muchas comunicaciones diferentes simultáneas. Es suficiente con que en ambos extremos de los conductores se tengan los filtros y circuitos oscilantes sintonizados para cada una de las frecuencias que son introducidas en el cable. Un ejemplo es la comunicación de datos y voz usando la línea eléctrica doméstica de corriente alterna.

Multiplexión en control automático: Para el control automático de muchos diferentes artefactos conectados a un par de conductores y estos a una central de control, si cada uno de los artefactos solo transmite su señal en una única frecuencia, es posible que la central diferencie la señal de cada uno de ellos y determinar así el estado de escanear o explorar su red y determinar el estado en que se encuentra cada uno de sus artefactos que controla. Por ejemplo, un tanque de agua puede tener un sensor de máximo nivel, tan simple como un flotador con un interruptor de contactos. Este estado, abierto/cerrado (y muchos otros de un sistema de bombeo) desconecta o conecta un circuito oscilador. Esta oscilación llega (o se interrumpe) en la central de control la cual, a su vez, realiza la conmutación correspondiente de detener o arrancar el motor según el nivel de agua en el depósito. Cuando es necesario controlar muchos parámetros y artefactos esta es una manera simple y económica ya que el cableado resultaría complejo y caro en caso de utilizarse más hilos conductores.

Transponder, transpondedor: es un dispositivo transmisor-respondedor, o sea, que emite una respuesta cuando recibe una señal de radio denominada interrogación o pregunta. Por ejemplo el transpondedor (activo) de una aeronave recibe una señal en una frecuencia, y transmite sus respuestas en otra frecuencia. En tráfico aéreo permite diferenciar e identificar cada aeronave en la pantalla del radar del controlador que, de no disponer de este sistema, solo se observaría un punto luminoso por cada objeto en vuelo. Como las respuestas que emite automáticamente cada aeronave puede aportar varios datos, permite tener información adecuada como para mantener distancias seguras entre aeronaves evitando colisiones. Sistemas similares se instalan en embarcaciones, satélites, etc., normalmente con separación a grandes distancias entre el transmisor (preguntador) y el respondedor. Los transponders pasivos normalmente tienen un alcance muy pequeño en el orden de un metro y menos, sin fuente de alimentación eléctrica propia. En estos, el "preguntador" es un escáner consistente en un generador de campo magnético que induce corriente en el solenoide de cobre del "respondedor" según se explicó más arriba.

En la época actual de las nuevas tecnologías y el control digital computarizado o inteligente, es muy frecuente encontrar que se está potenciando el uso de los circuitos osciladores los cuales clasifican como circuitos analógicos, pero la combinación: Multiplexión analógica + Análisis, procesamiento, actuación digital, es cada vez más amplio y explotado.

Véase también[editar]

Datos: Q732473
Multimedia: LC circuits / Q732473