Ecuación de movimiento
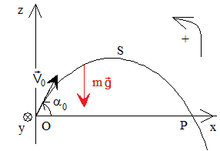
En física, una ecuación de movimiento es la formulación matemática que define la evolución temporal de un sistema físico en el espacio. Esta ecuación relaciona la derivada temporal de una o varias variables que caracterizan el estado físico del sistema, con otras magnitudes físicas que provocan los cambios en este.
En la dinámica del punto material, la ecuación de movimiento determina la posición futura de un objeto o partícula móvil en función de otras variables como, su velocidad, su aceleración, su masa y cuantas variables le puedan afectar en su movimiento junto con las condiciones iniciales. En otras áreas de la física como la mecánica de los medios continuos o la teoría de campos se habla de ecuación de movimiento en general para describir las ecuaciones de evolución o variación temporal del sistema.
Ecuaciones de movimiento en mecánica clásica[editar]
Históricamente el primer ejemplo de ecuación del movimiento que se introdujo en física fue la segunda ley de Newton para sistemas físicos compuestos de agregados partículas materiales puntuales. En estos sistemas el estado dinámico de un sistema quedaba fijado por la posición y velocidad de todas las partículas en un instante dado. Hacia finales del siglo XVIII se introdujo la mecánica analítica o racional, como generalización de las leyes de Newton aplicables a sistemas de referencia inerciales. Se concibieron dos enfoques básicamente equivalentes conocidos como mecánica lagrangiana y mecánica hamiltoniana, que pueden llegar a un elevado grado de abstracción y formalización en ecuaciones diferenciales.
Sistemas discretos[editar]
Un sistema discreto de partículas o de sólidos rígidos tiene un número finito de grados de libertad. Los ejemplos clásicos de ecuación del movimiento más conocidos son:
- La segunda ley de Newton que se usa en mecánica newtoniana:
- Las ecuaciones de Euler-Lagrange que aparecen en mecánica lagrangiana:
- Las ecuaciones de Hamilton que aparecen en mecánica hamiltoniana:
Sistemas continuos[editar]
Muchos sistemas de la mecánica clásica se modelizan como un medio continuo entre ellos formables y la mecánica de fluidos. Estos sistemas requieren ecuaciones de evolución temporal que involucran ecuaciones diferenciales en derivadas parciales.
Ecuaciones de movimiento en teoría de la relatividad[editar]
En la teoría de la relatividad existen dos tipos de entidades físicas, las partículas y los campos. Aunque en última instancia, tal como establece la teoría cuántica de campos, las partículas son campos materiales altamente localizados, en teoría de la relatividad se pueden tratar las partículas como entes físicos localizados en el espacio-tiempo. La distinción entre estos tipos de entidades físicas hace que en teoría de la relatividad existan dos tipos de ecuaciones de movimiento:
- Las ecuaciones de movimiento de las partículas materiales, que son la generalización relativista de las ecuaciones de la mecánica clásica.
- Las ecuaciones de "movimiento" o evolución temporal de los campos físicos.
Ecuaciones de movimiento de partículas[editar]
El análogo de la primera ley de Newton en teoría de la teoría de la relatividad postula que cuando sobre las partículas no actúa ninguna fuerza estas se mueven a lo largo de las geodésicas del espacio-tiempo, es decir, sobre las líneas más "rectas" posibles o de curvatura mínima. Cuando sobre las partículas actúa alguna fuerza, la ecuación del movimiento en términos de tiempo propio de la partícula, los símbolos de Christoffel dependientes de la curvatura del espacio tiempo, y la fuerza total sobre la partícula viene dada por:
Para una partícula moviéndose a través de un espacio-tiempo plano (), con velocidad pequeña respecto a la de la luz () la anterior ecuación se reduce a la segunda ley de Newton.
Ecuaciones de movimiento en teoría clásica de campos[editar]
Los sistemas físicos formados por un conjunto de partículas interactuantes de la mecánica clásica y los sistemas físicos de partículas relativistas sin interacción, son sistemas con un número finito de grados de libertad, cuyas ecuaciones de movimiento vienen dadas por ecuaciones diferenciales ordinarias como todos los ejemplos anteriores. Sin embargo, los campos físicos además de evolución temporal o variación en el tiempo, presentan variación en el espacio. Esa característica hace que los campos físicos se consideren informalmente como sistemas con un número infinito de grados de libertad. Las peculiaridades de los campos hacen que sus ecuaciones de "movimiento" o evolución temporal vengan dadas por ecuaciones en derivadas parciales en lugar de ecuaciones diferenciales ordinarias.
El campo físico más importante en el contexto de la teoría de la Relatividad Especial es el campo electromagnético, cuyas ecuaciones de evolución temporal vienen dadas por las ecuaciones de Maxwell. Estas ecuaciones pueden escribirse de diversas maneras y de diversas notaciones, aunque en el contexto de la teoría de la relatividad conviene escribirlas en forma explícitamente covariante en términos del tensor campo electromagnético . En esa forma, las ecuaciones se reducen a dos ecuaciones de la forma (unidades cgs):
Donde se ha usado el convenio de sumación de Einstein, son las componentes del cuadrivector densidad de corriente. En esas ecuaciones aparecen las coordenadas (donde c es la velocidad de la luz, t el tiempo, y (x,y,z) son las coordenadas cartesianas convencionales del espacio tridimensional. Así la evolución en el tiempo del campo electromagnético, si nos fijamos en un punto concreto del espacio viene medida por las derivadas respecto a la coordenada x<su>0</supo> = ct.
En el contexto de la teoría general de la relatividad aparece un problema adicional. La propia geometría del espacio-tiempo viene representada por un campo tensorial llamado tensor métrico. El propio campo gravitatorio es una manifestación de que la geometría del espacio-tiempo no es plana o euclídea. El campo gravitatorio de hecho es proporcional a la curvatura del espacio-tiempo. Las ecuaciones de evolución vuelven a ser ecuaciones diferenciales en derivadas parciales:
donde reaparecen los símbolos de Christoffel que aparecían en la ecuación del movimiento de las partículas. A diferencia de las ecuaciones del campo electromagnético, estas ecuaciones del campo gravitatorio o geometría del espacio-tiempo son ecuaciones no lineales debido a la presencia de términos que son el producto de dos Γ. Esto hace que las ecuaciones de Einstein del campo gravitatorio sean de difícil solución.
Ecuaciones de movimiento en mecánica cuántica[editar]
En mecánica cuántica existen diversos tipos de ecuación de movimiento para la función de onda según el tipo de problema o sistema cuántico estudiado. Los ejemplos más conocidos de ecuación del movimiento son:
Referencias[editar]
Bibliografía[editar]
- Landau & Lifshitz: Mecánica, Ed. Reverté, Barcelona, 1991. ISBN 84-291-4081-6.
- Landau & Lifshitz, Teoría clásica de los campos, Ed. Reverté, ISBN 84-291-4082-4.














![{\displaystyle \left[-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+U(\mathbf {r} )\right]\psi (\mathbf {r} ,t)=i\hbar {\frac {\partial \psi (\mathbf {r} ,t)}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b27038e09ea4f24353c7f2a15ba0523b11889db)
![{\displaystyle \left[{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}-\nabla ^{2}+\mu ^{2}\right]\psi =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01658acb075f1afc2902c5634c62fdaf6aeeafbc)
![{\displaystyle i\hbar {\frac {d\psi }{dt}}=\left[c\sum _{i=1}^{3}\alpha _{i}p_{i}+\alpha _{0}mc^{2}\right]\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/735fc4b857b229c30073896de01685ed6a1dcf38)