Diferencia entre revisiones de «Circuito»
m Revertidos los cambios de 201.171.196.71 a la última edición de Diegusjaimes |
|||
| Línea 147: | Línea 147: | ||
Este caso es el que se presenta, por ejemplo, a la hora de ampliar la escala de un [[voltímetro]], donde R1 sería la resistencia de la bobina voltimétrica y R2 la resistencia de ampliación de escala. |
Este caso es el que se presenta, por ejemplo, a la hora de ampliar la escala de un [[voltímetro]], donde R1 sería la resistencia de la bobina voltimétrica y R2 la resistencia de ampliación de escala. |
||
Qué es un divisor de tensión? |
|||
Aquí va a descubrir y aprender pero, no tenga demasiada prisa. Lea y practique con lo que aquí se explica y siga los pasos que se dan en la lección. El diagrama siguiente, muestra una resistencia que depende de la luz conocida como LDR (Resistencia Dependiente de la Luz), junto con su símbolo de circuito: |
|||
La parte sensible a la luz del LDR es una pista 'ondulada' de sulfuro de cadmio. La energía de la luz que incide en esta zona, acciona la avalancha de los portadores de carga en este material (conducción), de modo que bajará su resistencia mientras que el nivel de la iluminación se mantenga. |
|||
Un sensor de luz, utiliza una LDR como parte de un divisor del tensión. |
|||
Nota: Voy a utilizar un termino en la denominación de los componentes del que espero que nos ayude en la comprensión. Utilizaré los términos 'arriba' y 'bajo' para las resistencias del divisor, por su posición en el grafico y como digo, espero que esto nos ayude a recordar. |
|||
Circuito esencial de un divisor de tensión, también llamado divisor de potencial o divisor de voltaje y su fórmula: |
|||
F1[F1] |
|||
Como se puede ver, dos resistencias están conectadas en serie con la tensión de entrada Vin, que puede ser o no, la tensión de la fuente de alimentación, conectada a Rarriba, la otra resistencia Rbajo conectada a masa. La tensión de la salida Vout, es el voltaje a extremos de Rbajo y viene dada por: |
|||
F2 [F2] |
|||
Normalmente conocemos la tensión de entrada Vin, la tensión de salida en algunos casos y la corriente que se necesita en la salida del divisor, por lo tanto podemos plantear un ejemplo de utilidad como el siguiente: |
|||
Tenemos una tensión de entrada de 9V, necesitamos una tensión de salida de 5V. Calcular las resistencias necesarias para crear un divisor de tensión de estas características. F3 |
|||
Observemos estas dos formulas de la derecha, entre ellas podemos ver la semejanza, en donde los términos del quebrado se intercambia tensión (V) por resistencia (R). Podemos deducir Va = 4V y Vb = 5V. También podemos deducir lo siguiente: |
|||
(Ra+Rb) x Vout = Rb x Vin [F3] |
|||
Suponiendo que la corriente en vacío a través de Ra y Rb sea de 0'02A, optemos el valor para el conjunto Ra+Rb = 450 Ohms, sustituimos los valores conocidos y tenemos: |
|||
(450) x 5 = Rb x 9; despejando Rb, tememos que: Rb = 2250 / 9 = 250 Ohms, ahora podemos saber que Ra = 200 Ohms |
|||
La potencia o vataje de Ra se hallará dependiendo de la corriente que se necesite en la salida más la de drenaje (0'02A). Para comprobar los cálculos, aplicaremos la formula [F1], lo que nos muestra su validez. |
|||
Ésta es una fórmula verdaderamente útil que conviene aprender y recordar. |
|||
Puede ayudarnos a recordar que, Rbajo en la ecuación aparece en la parte superior de la fórmula porque la tensión de salida (Vout) se mide a extremos de Rbajo. |
|||
¿Qué sucede si una de las resistencias en el divisor de tensión es substituida por una LDR? En el siguiente circuito, Rarriba es una resistencia de 10k, y se utiliza una LDR como Rbajo: |
|||
Divisor con LDR abajo |
|||
Supongamos que la LDR tiene una resistencia de 500 W = 0.5 kW en luz brillante y 200 kW en la oscuridad (ambos valores son razonables). |
|||
Cuando la LDR está en la luz, Vout será: |
|||
0,5 |
|||
Vout= -------------- x 9 V = 0,43 V |
|||
0,5 + 10 |
|||
Y en la penumbra, Vout será: |
|||
200 |
|||
Vout= -------------- x 9 V = 8,57 V |
|||
200 + 10 |
|||
Es decir este circuito da una tensión BAJA en la salida cuando el LDR está en la luz, y una tensión ALTA cuando la LDR está en la penumbra. El circuito divisor de tensión dará una tensión de la salida que cambia con la iluminación, de forma inversamente proporcional a la cantidad de luz que reciba. |
|||
Un sistema de sensor que funcione como esto se podría pensar como 'sensor de oscuridad' y se podría utilizar para controlar los circuitos de iluminación que se encienden (conectan) automáticamente por la tarde. |
|||
Quizás esto no le parezca un circuito emocionante, pero puede pensar en aplicaciones que usen un sensor como divisor de tensión. Hay realmente otra manera de hacer trabajar a los sistemas con sensores de luz. |
|||
Aquí está el divisor de voltaje constituido por la LDR que sustituye la resistencia de Rarriba: |
|||
Divisor con LDR arriba |
|||
¿Qué efecto tiene esto en la Vout? |
|||
La acción invierte el circuito es decir, Vout llega a ser ALTA, cuando la LDR está en la luz, y BAJA cuando el LDR está en la oscuridad. Substituya los valores apropiados en el fórmula del divisor del voltaje para convencerse de que esto es verdad. |
|||
Repaso: |
|||
1. |
|||
Aplique la fórmula para calcular la Vout de un divisor de tensión. |
|||
2. |
|||
¿Cuál es la alternativa conocida para esta clase de circuito? |
|||
3. |
|||
¿La resistencia de una LDR baja o sube con luz brillante? Explique su respuesta. |
|||
4. |
|||
Calcule Vout para el circuito mostrado abajo, asumiendo que el LDR tiene una resistencia de 2 kW. |
|||
5. |
|||
¿En este circuito, Vout aumenta o disminuye con luz brillante? |
|||
6. |
|||
¿Cómo se podría invertir la función de este circuito? |
|||
Respuestas |
|||
Sensores de temperatura |
|||
Una resistencia que es sensible a la temperatura es lo que se llama un termistor, una definición más técnica sería: A la resistencia con coeficiente de temperatura negativo, conocida como termistor, NTC o con coeficiente de temperatura positivo PTC, a este tipo de resistencias la temperatura ambiente les afecta de modo que modifican su valor dentro de unos parámetros. Hay varios tipos de encapsulado: |
|||
Tipos de Termistores |
|||
La resistencia de la mayoría de los tipos comunes de termistor disminuye mientras que se eleva la temperatura. Se llaman de, coeficiente negativo de temperatura o termistores NTC. Observe el -t° al lado del símbolo del circuito. Un termistor NTC típico se hace usando materiales de óxido de metal semiconductor. Los semiconductores tienen la característica de ofrecer la mitad de la resistencia entre los conductores y los aislantes. Mientras más se eleva la temperatura, más portadores de carga están disponibles y esto causa la caída del valor de la resistencia. |
|||
Aunque es menos utilizado, es posible fabricar termistores de temperatura de coeficiente positivo o PTC. Éstos se hacen de diversos materiales y muestran un aumento de resistencia que varía con temperatura. |
|||
¿Cómo podríamos hacer un circuito con este sensor, para su uso en una alarma de incendios? Utilizaremos un circuito que entregue una tensión alta cuando se detecten las condiciones de temperatura caliente. Necesitamos poner un divisor de tensión con un termistor NTC en la posición que ocupa Rarriba: |
|||
¿Cómo podríamos hacer un circuito con un sensor para detectar temperaturas de menos de 4°C para advertir a motoristas que pueda haber hielo en la carretera? Usaremos un circuito que dé una tensión alta en condiciones frías. Necesitamos un divisor de voltaje con el termistor en lugar de Rbajo: |
|||
Este último ejemplo nos plantea una interesante pregunta: ¿Cómo saber qué valor de tensión de Vout se va a conseguir con 4°C? Vea el siguiente gráfico de las característica de un termistor: |
|||
En el eje Y, se representa la resistencia con una escala logarítmica. Ésta es una manera de comprimir el gráfico de modo que sea más fácil ver cómo cambia la resistencia. Entre 100 W y 1000 W, cada división horizontal corresponde a 100 W. Por otra parte, entre 1000 W y 10000 W, cada división corresponde a 1000 W. Y sobre 10000 W, representa 10000 W cada división. |
|||
Como se puede apreciar, este termistor tiene una resistencia que varía de alrededor 70 k W en 0°C a cerca de 1 kW a 100°C. Los catálogos de los suministradores, dan generalmente la resistencia a 25°C, que en este caso será 20 kW. Generalmente, los catálogos también especifican un ' beta ' o ' B-valor '. Cuando se especifican estos dos números, es posible calcular un valor aproximado para la resistencia del termistor en cualquier temperatura de la ecuación particular: |
|||
RT = R To x e |
|||
(B((1/T) - (1/T0))) |
|||
Donde: |
|||
RT es la resistencia a temperatura T en grados Kelvin (k = ºC + 273) |
|||
RTo es la resistencia de referencia a una temperatura To en Kelvin. Cuando la temperatura de la referencia es 25 ºC, T0 = 25+273. |
|||
e es la base del logaritmo natural, elevada a la potencia [B((1/T) - (1/T0))] en esta ecuación. |
|||
B es el 'B-valor' especificado para este termistor. |
|||
Quizás no necesites aplicar esta ecuación en este momento, pero es útil saber que, la información proporcionada en los catálogos es suficiente para permitir que podamos calcular el funcionamiento del termistor. Con una hoja de Excel por ejemplo, es posible generar las curvas características para cualquier termistor, calculando los valores de la resistencia para una gama de temperaturas dadas. |
|||
Con RTo = 20 kW y B = 4200, saltos de resistencia a partir de 0 a 10°C están como sigue: |
|||
Según el gráfico, la resistencia para 4°C, se puede estimar poco menos de 60 kW. Mediante la ecuación se ha calculado el valor exacto, que es 58.2 kW. |
|||
El mayor equilibrio de Vout en un divisor de tensión, se obtiene cuando ambos valores Ra y Rb son IGUALES. |
|||
Con estos datos elegimos el que da un valor para Rarriba cerca de 58.2 kW, lo que hará del divisor de tensión para la alarma por hielo, más sensible cerca de los 4°C. El valor más cercano (E12/E24) es 56 kW. Esto es importante porque los saltos grandes de Vout hacen más fácil diseñar los otros subsistemas en la alarma para hielo, de modo que las temperaturas por debajo de 4°C podrán ser detectadas con mayor fiabilidad. |
|||
Los dispositivos sensores varían considerablemente su resistencia, se puede aplicar esta regla para cerciorarse de que los divisores de tensión que construya serán siempre tan sensibles como sea posible en el punto crítico. |
|||
Los termistores vuelven a utilizarse en lugares en los que puede que no se imagine. Se utilizan extensivamente en coches, por ejemplo en: |
|||
* |
|||
Inyección electrónica de combustible, en la cual la entada de aire, la mezcla aire/combustible y las temperaturas del agua que le enfría, se supervisan para ayudar a determinar la concentración del combustible para la inyección óptima. |
|||
* |
|||
Controles de temperatura del aire acondicionado y de asientos en vehículos. |
|||
* |
|||
Los indicadores de alertas, tales como temperaturas de aceite y de líquido, nivel de aceite y turbo-cargador. |
|||
* |
|||
Control del motor de ventilador, basado en la temperatura del agua que se enfría. |
|||
* |
|||
Sensores de escarcha, para la medida de la temperatura exterior. |
|||
* |
|||
Sistemas acústicos. |
|||
Los termistores se utilizan para medir las temperaturas superficiales y profundas del mar para ayudar a supervisar corrientes del océano en el efecto EL NIÑO. Obviamente, los termistores se utilizan para medir flujo de aire, por ejemplo en la supervisión de la respiración en bebés prematuros, entre otras aplicaciones. |
|||
Ejemplo práctico. |
|||
Cuando el ventilador de nuestro computador se para, cosa que es bastante habitual por el uso continuado, se seca la grasa del eje y llega a pararse o se desgasta el soporte del eje, produce el típico ruido poco antes de estropearse definitivamente. Para evitar que se queme algún componente de considerable costo, necesitamos un detector de temperatura que nos avise de tal circunstancia. |
|||
Necesitamos un detector de temperatura que active un sonido de alerta que nos avise, utilizaremos un termistor NTC, un circuito integrado de bajo coste el 555 y unos pocos componentes asociados para esta práctica: |
|||
En el esquema anterior cuando la temperatura de la CPU supera el límite establecido por la NTC, se produce un aumento de la tensión en la patilla 2, lo que produce el disparo del circuito integrado que está configurado como oscilador, generando una frecuencia audible que es amplificada por el transistor a su salida por la patilla 3 y que podemos oír en el altavoz, además mediante el diodo led de la salida, nos indicará de forma visual que la temperatura está por encima de lo previsto. |
|||
Repaso: |
|||
1. |
|||
Distinguir entre los termistores el ntc y ptc. ¿Qué sucede a la resistencia de cada tipo cuando la temperatura aumenta? |
|||
2. |
|||
Un extractor de invernadero debe funcionar automáticamente si la temperatura excede 40°C. Estimar la resistencia del termistor en 40°C de la curva característica del siguiente gráfico: |
|||
3. |
|||
Trace un circuito divisor de tensión que aumente su Vout según lo haga la temperatura. ¿Cual debe ser el valor de la resistencia fija para una sensibilidad máxima a 40°C? |
|||
Respuestas |
|||
Divisor con diodo Zener |
|||
No voy a entrar a describir que es y como se comporta un diodo zener, ya que no es este el motivo de este artículo, son necesarios unos conocimientos básicos para continuar. Esta es la aplicación más común utilizada por la mayoría de técnicos en los talleres de reparación, cuando tienen la necesidad de obtener una tensión no prevista y en su lugar disponen de una tensión superior, en los casos de tensiones inferiores a 5V o fuera del margen de los reguladores comerciales, se ven obligados a usar un divisor de tensión en el que usan un diodo zener de la tensión adecuada al caso. Veamos como proceder en un caso concreto. |
|||
EL circuito al que haré referencia se puede ver a la derecha. En ella, la Rarriba (R limitadora) ha de ser calculada entre los valores de tensión mínimos y máximo para que la tensión en la salida Rcarga se mantenga constante dentro de los valores de entrada. Eligiendo la resistencia Rarriba y las características del diodo zener, se puede lograr que la tensión en la carga Rcarga permanezca prácticamente constante que, es lo que nos interesa. |
|||
Veamos como elegir la resistencia limitadora Rarriba adecuada hay que calcular primero cuál puede ser su valor Rmáximo y Rmínimo, después elegiremos una resistencia R que cumpla con los valores calculados. |
|||
Donde: |
|||
1. Rmin, valor mínimo de la resistencia limitadora. |
|||
2. Rmax, valor máximo de la resistencia limitadora. |
|||
3. Vinmax, valor máximo de la tensión de entrada. |
|||
4. Vinmin, valor mínimo de la tensión de entrada. |
|||
5. Vz, tensión Zener. |
|||
6. Icmin, mínima intensidad que puede circular por la carga, |
|||
si la carga se desconecta, Icmin tomará el valor 0. |
|||
7. Icmax, máxima intensidad que soporta la carga. |
|||
8. Izmax, máxima intensidad que soporta el diodo Zener. |
|||
9. Izmin, mínima intensidad del diodo zener para mantener su |
|||
su zona zener o conducción en inversa. |
|||
Según esto, obsérvese que en el punto (6) si se desconecta la carga la intensidad Icmin tiende a 0, lo cual repercute en el sobrecalentamiento del diodo zener haciendo peligrar su integridad, por lo que se recomienda utilizar una resistencia en paralelo al diodo zener para que no se produzca este efecto negativo. |
|||
Esta resistencia puede calcularse considerando una corriente de paso cercana a la mínima del diodo zener para que se mantenga en la llamada zona zener de donde toma su nombre. |
|||
Caso práctico: Disponemos de una Vin de 5V, necesitamos una tensión para activar un circuito a 3V3 que consume 500mA, debemos calcular la R limitadora para que mediante un diodo zener de 3V3 nos entregue en la salida los 3V3 y si por cualquier motivo la carga se desconecta que no peligre el diodo zener. |
|||
Aplicando las formulas descritas en este caso, sólo usaremos un calculo, el de Rmáxima y obtendremos una resistencia de 3R3, es decir, de 3'3 W. Sin embargo, al conectar la tensión de 5V a la entrada y sin aplicar ninguna carga, se observa que hay un consumo de cerca de 500mA, cuando no hay carga, también se descubre que el diodo zener está realmente muy caliente y seguro que nos acordaremos de cuanto. |
|||
Ahora, pongamos una resistencia que limite este consumo, paradójicamente esta resistencia, no se pone en serie, sino en paralelo. Si calculamos el valor para una corriente de paso de 0'003 A (3mA) con una tensión de 3'3V por aproximación usaremos una resistencia de 1k W. Y ¡¡Voila!! Ahora, el consumo ha bajado a 100mA. El diodo zener no se calienta y el consumo no es excesivo, lo que se pedía. |
|||
El puente Wheatstone |
|||
Sir Charles Wheatstone era un científico versátil y con talento. Él inventó la concertina, experimentó con fotografía estereoscópica e inventó el estereoscopio e hizo una parte importante en el desarrollo temprano de las comunicaciones del telégrafo. Él no reclamó haber inventado el circuito nombrado después con su nombre, sino que estaba entre los primeros en explotar el circuito con eficacia en la fabricación de resistencias patrón. |
|||
¿Así que, que es un puente de Wheatstone? Veamos, este es el circuito: |
|||
Es obvio que el circuito consiste en dos divisores de tensión. Suponga que RX es un valor de la resistencia desconocida. Si ajustamos RC hasta que Va del segundo divisor de tensión es igual a Vb del divisor de tensión del brazo que contiene RX. Cuando los valores de Va y Vb son iguales, se dice que el puente está equilibrado. El punto de equilibrio puede ser detectado conectando un voltímetro o un amperímetro a través de los terminales de salida entre Va y Vb. Ambas clases de medida dan una lectura cero cuando se alcanza el equilibrio. |
|||
En un circuito equilibrado, el cociente RX/RA es igual al cociente de RB/RC . |
|||
RA x RB |
|||
RX = ------------------ |
|||
RC |
|||
Es decir si los valores del RA, de RB y de RC se saben, es fácil calcular RX. En instrumentos, basados en el puente de Wheatstone, el RA y el RB son fijos y RC es ajustable en una escala que varía de una manera tal que el valor de RX se puede leer directamente. |
|||
Ajuste de temperatura. |
|||
Para el ajuste de un puente Wheatstone como termómetro (siempre dentro de unos parámetros), la sonda de la NTC, se introduce en un vaso con agua y hielo (temperatura conocida 0ºC), la resistencia ajustable Rc se regula de modo que el polímetro marque 0V, esto se debe realizar con varios intentos para que el ajuste sea lo más exacto posible. Cuando se consiga el ajuste, tendremos calibrado el termómetro, con la seguridad relativa de conocer la temperatura que tiene un cuerpo o el ambiente. |
|||
Actualmente, los circuitos puente de Wheatstone no se utilizan generalmente para medir valores de resistencia, sino que se utilizan para diseñar los circuitos sensores. |
|||
Para la detección de cambios en la presión del aire, debido a los cambios repentinos en la altitud, se usa un instrumento llamado variómetro como ayuda en el vuelo de planeadores. El variómetro alerta al piloto del planeador, de las corrientes aéreas ascendentes o las térmicas. Circundando o dentro de una térmica, el piloto puede ganar altura y permanecer en vuelo por más tiempo. |
|||
Un tipo de variómetro utiliza termistores para supervisar los cambios de presión: |
|||
Los cambios de altitud son los que producen los cambios del flujo de aire. Un elemento calefactor calienta el aire que llega de la corriente del flujo a distintas temperaturas, un sensor alto por agua y en sentido descendiente el elemento de calefacción dependiendo del índice del flujo de aire. |
|||
Los sensores de termistor son parte del puente de Wheatstone: |
|||
Cuando el instrumento es primer instalado, preestablezca el resistor se ajusta según la salida cero. La ventaja del puente de Wheatstone es que solamente las diferencias de la temperatura entre los dos sensores pondrán el puente de balance. Las condiciones atmosféricas frías o calientes afectan a ambos sensores igualmente. El flujo de aire en/de la cámara de referencia tiene un efecto opuesto en los dos sensores: uno será calentado por la corriente de aire, mientras que el otro se enfría. Consecuentemente, la salida cambiará por más que se haya ajustado el sensor del dispositivo. |
|||
Por cierto, los circuitos de puente de Wheatstone se suponen difíciles de entender. El circuito se dibuja generalmente como un puente rectificador: |
|||
Es poco probable pensar en dos divisores de tensión, pero una vez que describamos cómo se comporta el circuito será fácil de seguir. |
|||
Repaso: |
|||
1. Calcular el valor de RX en el puente de Wheatstone del siguiente circuito. |
|||
2. ¿Qué ventajas ofrecen los sistemas sensores usando los circuitos de puente de Wheatstone? |
|||
Respuestas |
|||
Sensores de sonido |
|||
Otro nombre para un sensor de sonidos es un micrófono. El diagrama muestra un micrófono denominado electret: |
|||
Como se debe saber, para que los micrófonos electret trabajen correctamente, necesitan de una tensión de alimentación, generalmente alrededor 1.5 V a través. Un circuito adecuado para el uso con una fuente de 9 V es el siguiente: |
|||
Los 4.7 kW y las resistencias de 1 kW forman un divisor de tensión que proporciona 1.6 V a través del micrófono. Las ondas acústicas generan pequeños cambios en la tensión, generalmente en la gama de 10-20 mV. Para separar estas pequeñas señales de 1.6 V, se utiliza las características de un condensador, separando así la componente continua de la alimentación. |
|||
Señales con los interruptores. |
|||
Como ya se ha dicho, cuando se utiliza un interruptor para proporcionar una entrada a un circuito como presionar un interruptor generalmente genera un pico de tensión. Es el pico de tensión que genera el propio circuito con la acción de puesta en marcha. ¿Qué se necesita para generar una señal de tensión con el interruptor? . . . |
|||
Se necesita un divisor de tensión. El circuito se puede construir con cualquiera de las dos maneras: |
|||
La resistencia bajo en el primer circuito fuerza a Vout, llegando a nivel CERO, hasta que se acciona el pulsador. Este circuito entrega una tensión alta, cuando se presiona el pulsador. Un valor para la resistencia de 10 kW es adecuada. |
|||
En el segundo circuito, la resistencia Rarriba fuerza a nivel ALTO a Vout, mientras no se actúe sobre el pulsador. Al presionar el pulsador, se conecta Vout directamente con 0 V. Es decir, este circuito entrega un nivel BAJO cuando se presiona el pulsador. |
|||
En los circuitos de proceso señales de lógica, una tensión BAJA se llama 'lógica 0' o ' 0 ', mientras que una tensión ALTA se llama 'lógica 1' o ' 1 '. Estos circuitos de divisor de tensión son perfectos para proporcionar las señales de entrada para los sistemas de lógica. |
|||
Algunas clases de interruptores que se podrían utilizar. Una variedad de pulsadores que llaman pulsador táctil miniatura. Éstos son unos pulsadores pequeños que encajan bien en la placas estándar para montajes de prototipos: |
|||
Como se puede ver, el pulsador tiene cuatro terminales que están conectados a pares por las tiras internas de metal. Al presionar el botón se tiende un puente sobre los contactos y cierra el contacto. Los terminales extras son útiles al diseñar las placas de circuito impreso para teclados y también para el pulsador de parada o reset. |
|||
Hay otros tipos de pulsadores que puede ser que nos interese utilizar en una configuración de divisor de tensión. Podemos incluir los interruptores magnéticos de láminas llamados reed, los interruptores de nivel y los detectores de presión, todos para usos con alarmas contra ladrones. |
|||
Los circuitos electrónicos acumulan sistemas y se idean en términos de ENTRADA, PROCESO, SALIDA. Entre los sistemas, se transfieren las señales. Estas señales se transfieren casi siempre como voltajes que varían. Esto hace inevitable que los circuitos electrónicos incluyan los divisores de tensión como parte integral de su estructura. |
|||
Los divisores del voltaje no son un poco importantes justo, ellos son fundamentales a una comprensión de circuitos electrónicos. Una vez que usted haya comenzado a buscarlos, usted los encontrará por todas partes. |
|||
Repaso: |
|||
1. |
|||
Un interruptor de láminas reed se cierra cuando se coloca cerca un imán. En un sistema de alarma, el imán está fijado a la parte móvil de una puerta o ventana, mientras que el interruptor reed está fijado al marco. Vout debe ser BAJO cuando la puerta o la ventana, esta cerrada y debe pasar a ALTO cuando se abre la puerta o la ventana. ¿Cuál de los dos circuitos divisor de tensión mostrados nos dará este resultado? |
|||
2. Sugerir un valor para Rarriba y Rbajo en estos circuitos. |
|||
3. |
|||
¿Cómo se podrían incluir varios interruptores reed en el mismo circuito divisor de tensión, para obtener una tensión alta, cuando de los interruptores reed estén abiertos? |
|||
Respuestas |
|||
Conclusiones. |
|||
Los circuitos electrónicos se componen de subsistemas o circuitos dedicados y se piensa en términos de ENTRADA, PROCESO, SALIDA. Entre estos sistemas se transfieren las distintas señales. Estas señales se transfieren casi siempre como tensiones que cambian. Esto hace inevitable que los circuitos electrónicos incluyan los divisores de tensión similares a los estudiados, como parte integral de su estructura. |
|||
Los divisores de tensión justamente no son poco importantes, yo diría que son fundamentales en la comprensión de circuitos electrónicos. |
|||
Una vez que hayamos empezado a buscarlos entre los circuitos habituales que manejamos, los encontraremos por todas partes. Ahora, en pocos días, después de haber leído este tema, nos encontraremos con los divisores de tensión en cada porción de circuito en el que indaguemos, eso no es malo, sin embargo es bueno y conveniente que repasemos la base, es decir la formula a aplicar en cada caso. |
|||
Si tiene alguna duda (sinceramente espero que no), recuerde que puede comunicarse con la administración para ampliar la parte que no tenga clara, al menos intentaremos darle respuesta a sus dudas. |
|||
Como siempre, comentarios, criticas y sugerencias para mejorar este artículo, son bienvenidos y apreciados. |
|||
=== Divisor de intensidad === |
=== Divisor de intensidad === |
||
Revisión del 00:15 7 abr 2010
Se denomina circuito eléctrico a una serie de elementos o componentes eléctricos o electrónicos, tales como resistencias, inductancias, condensadores, fuentes, y/o dispositivos electrónicos semiconductores, conectados eléctricamente entre sí con el propósito de generar, transportar o modificar señales electrónicas o eléctricas. En la figura podemos ver un circuito eléctrico, sencillo pero completo, al tener las partes fundamentales:
| ||||||||
| Circuito abierto. | ||||||||
| ||||||||
| Circuito cerrado. |
- Una fuente de energía eléctrica, en este caso la pila o batería.
- Una aplicación, en este caso una lámpara incandescente.
- Unos elementos de control o de maniobra, el interruptor.
- Un instrumento de medida, el Amperímetro, que mide la intensidad de corriente.
- El cableado y conexiones que completan el circuito.
Un circuito eléctrico tiene que tener estas partes, o ser parte de ellas.
Clasificación
Los circuitos eléctricos se clasifican de la siguiente forma:
Por el tipo de señal:
- De corriente continua
- De corriente alterna
- Mixtos
Por el tipo de régimen:
- Periódico
- Transitorio
- Permanente
Por el tipo de componentes:
- Eléctricos: Resistivos, inductivos, capacitivos y mixtos
- Electrónicos: digitales, analógicos y mixtos
Por su configuración:
Partes de un circuito
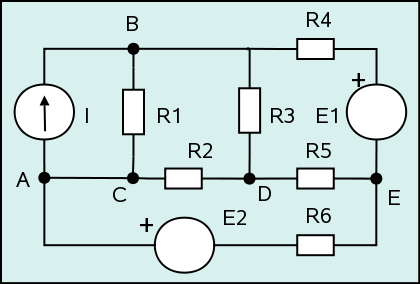
Para analizar un circuito deben de conocerse los nombres de los elementos que lo forman. A continuación se indican los nombres más comunes, tomando como ejemplo el circuito mostrado en la figura 1.
- Conductor: hilo de resistencia despreciable (idealmente cero) que une eléctricamente dos o más elementos.
- Generador o fuente: elemento que produce electricidad. En el circuito de la figura 1 hay tres fuentes, una de intensidad, I, y dos de tensión, E1 y E2.
- Nodo: punto de un circuito donde concurren varios conductores distintos. En la figura 1 se pueden ver cuatro nodos: A, B, D y E. Obsérvese que C no se ha tenido en cuenta ya que es el mismo nodo A al no existir entre ellos diferencia de potencial (VA - VC = 0).
- Rama: conjunto de todos los elementos de un circuito comprendidos entre dos nodos consecutivos. En la figura 1 se hallan siete ramales: AB por la fuente, AB por R1, AD, AE, BD, BE y DE. Obviamente, por un ramal sólo puede circular una corriente.
Circuito analógico
Muchas de las aplicaciones electrónicas analógicas, como los receptores de radio, se fabrican como un conjunto de unos cuantos circuitos más simples. Seguidamente se indican algunos ejemplos.
- Multiplicador analógico
- Amplificador electrónico
- Filtro analógico
- Oscilador electrónico
- Lazo de seguimiento de fase
- Temporizador
- Conversor de potencia
- Fuente de alimentación
- Adaptador de impedancia
- Amplificador operacional
- Comparador
- Mezclador electrónico
Circuito digital
Las computadoras, los relojes electrónicos o los controladores lógicos programables, usados para controlar procesos industriales, son ejemplos de dispositivos que se fabrican con circuitos digitales.
La estructura de los circuitos digitales no difieren mucho de los analógicos pero su diferencia fundamental es que trabajan con señales discretas con dos únicos valores posibles. Seguidamente se indican varios ejemplos de bloques básicos y familias lógicas.
|
Bloques: |
Dispositivos integrados: |
Familias Lógicas: |
Circuitos de señal mixta
Este tipo de circuitos, también conocidos como circuitos híbridos, contienen componentes analógicos y digitales, y se están haciendo cada vez más comunes. Los conversores analógico-digital y los conversores digital-analógico son los principales ejemplos.
Circuitos de corriente continua

En este punto se describirán los principales circuitos en corriente continua así como su análisis, esto es, el cálculo de las intensidades, tensiones o potencias.
Divisor de tensión
Dos o más resistencias conectadas en serie forman un divisor de tensión. De acuerdo con la segunda ley de Kirchhoff o ley de las mallas, la tensión total es suma de las tensiones parciales en cada resistencia, por lo que seleccionando valores adecuados de las mismas, se puede dividir una tensión en los valores más pequeños que se deseen. La tensión en bornes de la resistencia , en un divisor de tensión de n resistencias cuya tensión total es V, viene dada por:
En el caso particular de un divisor de dos resistencias (figura 2 a), es posible determinar las tensiones en bornes de cada resistencia, VAB y VBC, en función de la tensión total, VAC, sin tener que calcular previamente la intensidad. Para ello se utilizan las siguientes ecuaciones de fácil deducción:
Este caso es el que se presenta, por ejemplo, a la hora de ampliar la escala de un voltímetro, donde R1 sería la resistencia de la bobina voltimétrica y R2 la resistencia de ampliación de escala.
Divisor de intensidad
Dos o más resistencias conectadas en paralelo forman un divisor de intensidad. De acuerdo con la primera ley de Kirchhoff o ley de los nudos, la corriente que entra en un nudo es igual a la suma de las corrientes que salen. Seleccionando valores adecuados de resistencias se puede dividir una corriente en los valores más pequeños que se deseen.
En el caso particular de un divisor de dos resistencias (figura 2 b), es posible determinar las corrientes parciales que circulan por cada resistencia, I1 e I2, en función de la corriente total, I, sin tener que calcular previamente la caída de tensión en la asociación. Para ello se utilizan las siguientes ecuaciones de fácil deducción:
Este caso es el que se presenta, por ejemplo, a la hora de ampliar la escala de un amperímetro, donde R1 sería la resistencia de la bobina amperimétrica y R2 la resistencia shunt.
Red con fuente única

Se trata de una red de resistencias alimentadas con una sola fuente (figura 3). Para su análisis se seguirán, en general, los siguientes pasos:
- Se calcula la resistencia equivalente de la asociación.
- Se calcula la intensidad, I, que suministra la fuente,
- Se calculan las intensidades y tensiones parciales.
A modo de ejemplo de lo expuesto, se analizará el circuito de la figura 3 su poniendo los siguientes valores:
Resolución
1. Sea la resistencia equivalente de la rama superior del circuito
Y denominando Re a la resistencia equivalente:
2. A partir de la ley de Ohm se determina la intensidad, I, que proporciona la fuente:
3. A partir de la ley de Ohm:
R3 y R4 forman un divisor de intensidad para I1, por lo tanto
Red general

En el caso más general, el circuito podrá tener más de una fuente. El análisis clásico de este tipo de redes se realiza obteniendo, a partir de las leyes de Kirchhoff, un sistema de ecuaciones donde las incógitas serán las corrientes que circulan por cada rama. En general, el proceso a seguir será el siguiente:
- Se dibujan y nombran de modo arbitrario las corrientes que circulan por cada rama.
- Se obtiene un sistema de tantas ecuaciones como intensidades haya. Las ecuaciones se obtendrán a partir de:
- Se aplica la primera ley tantas veces como nudos haya menos uno.
- Se aplica la segunda ley a todas las mallas.
Como ejemplo, se analizará el circuito de la figura 4 considerando los siguientes valores:
Resolución
- Se consideran las intensidades dibujadas en el circuito.
- En el nudo A se cumple:
Y sumando las tensiones en ambas mallas (vea como determinar la polaridad de la caída de tensión de una resistencia en d. d. p.):
Dados los valores conocidos, tenemmos:
Ordenando las ecuaciones se obtiene el siguiente sistema
Cuyas soluciones son:
donde el valor negativo de I3 indica que la corriente circula en dirección contraria a como se ha dibujado en el circuito.
En análisis de circuitos se puede observar el método de las mallas que no simplifica el análisis de circuitos de este tipo.
Balance de potencias

Por balance de potencias de un circuito eléctrico se entiende la comprobación de que la suma algebraica de las potencias que generan o "absorben" las fuentes es igual a la suma de potencias que disipan los elementos pasivos. Para ello es necesario analizar previamente el circuito, esto es, determinar las corrientes que circulan por cada una de sus ramas así como las caídas de tensión en bornes de las fuentes de intensidad si las hubiere. Como ejemplo, se realizará el balance de potencias del circuito de la figura 5 considerando los siguientes valores:
Resolución
Aplicando la primera ley de Kirchhoff al nudo A y la segunda a la malla de la izquierda, se obtiene:
Operando se obtiene:
y la tensión en bornes de la fuente de intensidad
Terminado el análisis, se realiza el balance de potencias cuyos resultados se presentan en la siguiente tabla.
| Elementos activos | Elementos pasivos |
|---|---|
| |
|
Circuitos serie RL y RC


Los circuitos serie RL y RC (figura 6) tienen un comportamiento similar en cuanto a su respuesta en corriente y en tensión, respectivamente.
Al cerrar el interruptor S en el circuito serie RL, la bobina crea una fuerza electromotriz (f.e.m.) que se opone a la corriente que circula por el circuito, denominada por ello fuerza contraelectromotriz. Como consecuencia de ello, en el mismo instante de cerrar el interruptor (t0 en la figura 7) la intensidad será nula e irá aumentando exponencialmente hasta alcanzar su valor máximo, (de t0 a t1). Si a continuación, en el mismo instante de abrir S (t2 en la figura 7) se hará corto circuito en la red RL, el valor de no desaparecería instantáneamente, sino que iría disminuyendo de forma exponencial hasta hacerse cero (de t2 a t3).
Por otro lado, en el circuito serie RC, al cerrar el interruptor S (t0 en la figura 7), el condensador comienza a cargarse, aumentando su tensión exponencialmente hasta alcanzar su valor máximo E0 (de t0 a t1), que coincide con el valor de la f.e.m. E de la fuente. Si a continuación, en el mismo instante de abrir S (t2 en la figura 7) se hará corto circuito en la red RC, el valor de Eo no desaparecería instantáneamente, sino que iría disminuyendo de forma exponencial hasta hacerse cero (de t2 a t3).
En ambos circuitos se da por lo tanto dos tipos de régimen de funcionamiento (figura 7):
- Transitorio: desde t0 a t1 (carga) y desde t2 a t3 (descarga)
- Permanente: desde t1 a t2
La duración del régimen transitorio depende, en cada circuito, de los valores de la resistencia, R, la capacidad, C, del condensador y de la autoinductancia, L de la bobina. El valor de esta duración se suele tomar como , donde es la denominada constante de tiempo, siendo su valor en cada circuito:
Si R está en ohmios, C en faradios y L en henrios, estará en segundos.
Matemáticamente se pueden obtener las ecuaciones en régimen transitorio de cada circuito que se muestran en la siguiente tabla:
| Carga en RL | Descarga en RL | Carga en RC | Descarga en RC |
|---|---|---|---|
Circuitos de corriente alterna
En el presente apartado se verán las caraterísticas de los circuitos básicos de CA senoidal que están formados por los componentes eléctricos fundamentales: resistencia, bobina y condensador (ver previamente su comportamiento en DC). En cuanto a su análisis, todo lo visto en los circuitos de corriente continua es válido para los de alterna con la salvedad que habrá que operar con números complejos en lugar de con reales. Además se deberán tener en cuenta las siguientes condiciones:
- Todas las fuentes deben ser sinusoidales y tener la misma frecuencia o pulsación.
- Debe estar en régimen estacionario, es decir, una vez que los fenómenos transitorios que se producen a la conexión del circuito se hayan atenuado completamente.
- Todos los componentes del circuito deben ser lineales, o trabajar en un régimen tal que puedan considerarse como lineales. Los circuitos con diodos están excluidos y los resultados con inductores con núcleo ferromagnético serán solo aproximaciones.
Circuito serie RL
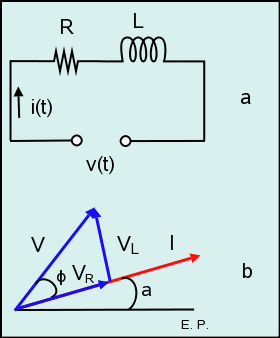
Supongamos que por el circuito de la figura 8a circula una corriente
Como está en fase y adelantada 90º respecto a dicha corriente, se tendrá:
Sumando fasorialmente ambas tensiones obtendremos la total V:
donde, y de acuerdo con el diagrama fasorial de la figura 8b, V es el módulo de la tensión total:
y φ el águlo que forman los fasores tensión total y corriente (ángulo de desfase):
La expresión representa la oposición que ofrece el circuito al paso de la corriente alterna, a la que se denomina impedancia y se representa Z:
En forma polar
con lo que la impedancia puede considerarse como una magnitud compleja, cuyo valor, de acuerdo con el triángulo de la figura 9, es:
Obsérvese que la parte real resulta ser la componente resistiva y la parte imaginaria la inductiva.
Circuito serie RC

Supongamos que por el circuito de la figura 10a circula una corriente
Como está en fase y retrasada 90º respecto a dicha corriente, se tendrá:
La tensión total V será igual a la suma fasorial de ambas tensiones,
Y de acuerdo con su diagrama fasorial (figura 10b) se tiene:
Al igual que en el apartado anterior la expresión es el módulo de la impedancia, ya que
lo que significa que la impedancia es una magnitud compleja cuyo valor, según el triángulo de la figura 11, es:
Obsérvese que la parte real resulta ser la componente resistiva y la parte imaginaria, ahora con signo negativo, la capacitiva.
Circuito serie RLC
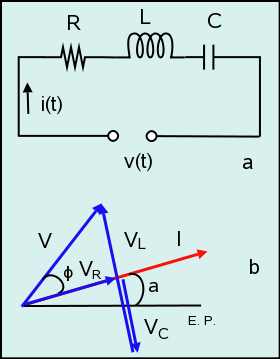
Razonado de modo similar en el circuito serie RLC de la figura 12 llegaremos a la conclusión de que la impedancia Z tiene un valor de
siendo φ
En el diagrama se ha supuesto que el circuito era inductivo (), pero en general se pueden dar los siguientes casos:
- : circuito inductivo, la intensidad queda retrasada respecto de la tensión (caso de la figura 12, donde φ es el ángulo de desfase).
- : circuito capacitivo, la intensidad queda adelantada respecto de la tensión.
- : circuito resistivo, la intensidad queda en fase con la tensión (en este caso se dice que hay resonancia).
Circuito serie general

Sean n impedancias en serie como las mostradas en la figura 13a, a las que se le aplica una tensión alterna V entre los terminales A y B lo que originará una corriente I. De acuerdo con la ley de Ohm:
donde es la impedancia equivalente de la asociación (figura 13c), esto es, aquella que conectada la misma tensión lterna, , demanda la misma intensidad, . Del mismo modo que para una asociación serie de resistencias, se puede demostrar que
lo que implica
y
Circuito paralelo general
Del mismo modo que en el apartado anterior, consideremos "n" impedancias en paralelo como las mostradas en la figura 13b, a las que se le aplica una tensión alterna "V" entre los terminales A y B lo que originará una corriente "I". De acuerdo con la ley de Ohm:
y del mismo modo que para una asociación paralelo de resistencias, se puede demostrar que
Para facilitar el cálculo en el análisis de circuitos de este tipo, se suele trabajar con admitancias en lugar de con impedancias.