Leyes de Kirchhoff
Las leyes de Kirchhoff [1][2][3] son dos igualdades que se basan en la conservación de la energía y la carga en los circuitos eléctricos.[4] Fueron descritas por primera vez en 1846 por Gustav Kirchhoff. Son ampliamente usadas en ingeniería eléctrica e ingeniería electrónica.
Ambas leyes de circuitos pueden derivarse directamente de las ecuaciones de Maxwell, pero Kirchhoff precedió a Maxwell y gracias a Georg Ohm su trabajo fue generalizado. Estas leyes son utilizadas para hallar corrientes y tensiones en cualquier punto de un circuito eléctrico.
Ley de corrientes de Kirchhoff[editar]

Esta ley también es llamada ley de nodos o primera ley de Kirchhoff [5][6] y es común que se use la sigla LCK para referirse a esta ley. La ley de corrientes de Kirchhoff nos dice que:
|
Esta fórmula es válida también para circuitos complejos:
La ley se basa en el principio de la conservación de la carga donde la carga en coulombios es el producto de la corriente en amperios y el tiempo en segundos.
Por definición, un nodo es un punto de una red eléctrica en el cual convergen tres o más conductores.
Esta primera ley confirma el principio de la conservación de las cargas eléctricas.
Densidad de carga variante[editar]
La LCK solo es válida si la densidad de carga se mantiene constante en el punto en el que se aplica. Considere la corriente entrando en una lámina de un condensador. Si uno se imagina una superficie cerrada alrededor de esa lámina, la corriente entra a través del dispositivo, pero no sale, violando la LCK. Además, la corriente a través de una superficie cerrada alrededor de todo el capacitor cumplirá la LCK entrante por una lámina sea balanceada por la corriente que sale de la otra lámina, que es lo que se hace en análisis de circuitos, aunque cabe resaltar que hay un problema al considerar una sola lámina.
Maxwell introdujo el concepto de corriente de desplazamiento para describir estas situaciones. La corriente que fluye en la lámina de un capacitor es igual al aumento de la acumulación de la carga y además es igual a la tasa de cambio del flujo eléctrico debido a la carga (el flujo eléctrico también se mide en Coulombs, como una carga eléctrica en el SIU). Esta tasa de cambio del flujo , es lo que Maxwell llamó corriente de desplazamiento :
Cuando la corriente de desplazamiento se incluye, la ley de Kirchhoff se cumple de nuevo. Las corrientes de desplazamiento no son corrientes reales debido a que no constan de cargas en movimiento, deberían verse más como un factor de corrección para hacer que la LCK se cumpla. En el caso de la lámina del capacitor, la corriente entrante de la lámina es cancelada por una corriente de desplazamiento que sale de la lámina y entra por la otra lámina.
Esto también puede expresarse en términos del vector campo al tomar la Ley de Ampere de la divergencia con la corrección de Maxwell y combinando la ley de Gauss, obteniendo:
Esto es simplemente la ecuación de la conservación de la carga en forma integral, dice que la corriente que fluye a través de una superficie cerrada es igual a la tasa de pérdida de carga del volumen encerrado (Teorema de Divergencia). La ley de Kirchhoff es equivalente a decir que la divergencia de la corriente es cero, para un tiempo invariante p, o siempre verdad si la corriente de desplazamiento está incluida en J.
Ley de tensiones de Kirchhoff[editar]

Esta ley es llamada también segunda ley de Kirchhoff,[7][8] se la conoce como la ley de las tensiones.
|
De igual manera que con la corriente, las tensiones también pueden ser complejos, así:
Esta ley se basa en la conservación de un campo potencial de energía. Dado una diferencia de potencial, una carga que ha completado un lazo cerrado no gana o pierde energía al regresar al potencial inicial.
Esta ley es cierta incluso cuando hay resistencia en el circuito. La validez de esta ley puede explicarse al considerar que una carga no regresa a su punto de partida, debido a la disipación de energía. Una carga simplemente terminará en el terminal negativo, en vez del positivo. Esto significa que toda la energía dada por la diferencia de potencial ha sido completamente consumida por la resistencia, la cual la transformará en calor. Teóricamente, y, dado que las tensiones tienen un signo, esto se traduce con un signo positivo al recorrer un circuito desde un mayor potencial a otro menor, y al revés: con un signo negativo al recorrer un circuito desde un menor potencial a otro mayor.
En resumen, la ley de tensión de Kirchhoff no tiene nada que ver con la ganancia o pérdida de energía de los componentes electrónicos (Resistores, capacitores, etc.). Es una ley que está relacionada con el campo potencial generado por fuentes de tensión. En este campo potencial, sin importar que componentes electrónicos estén presentes, la ganancia o pérdida de la energía dada por el campo potencial debe ser cero cuando una carga completa un lazo.[9]
Campo eléctrico y potencial eléctrico[editar]
La ley de tensión de Kirchhoff puede verse como una consecuencia del principio de la conservación de la energía. Considerando ese potencial eléctrico se define como una integral de línea, sobre un campo eléctrico, la ley de tensión de Kirchhoff puede expresarse como:
Que dice que la integral de línea del campo eléctrico alrededor de un lazo cerrado es cero.
Para regresar a una forma más especial, esta integral puede "partirse" para conseguir la tensión de un componente en específico.
Caso práctico[editar]
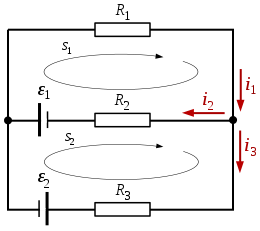
Asumiendo una red eléctrica consistente en dos fuentes y tres resistencias, disponemos la siguiente resolución: (antes de empezar, es necesario aclarar la convención de signos: si recorro la malla a favor de la corriente, el potencial asociado a la resistencia es negativo; caso contrario es positivo. Si recorro la fuente y hay una subida de potencial (de - a +), la fem es positiva; caso contrario es negativa.
De acuerdo con la primera ley de Kirchhoff (ley de los nodos), tenemos:
La segunda ley de Kirchhoff (ley de las mallas), aplicada a la malla según el circuito cerrado s1, nos hace obtener:
La segunda ley de Kirchhoff (ley de las mallas), aplicada a la malla según el circuito cerrado s2, por su parte:
Debido a lo anterior, se nos plantea un sistema de ecuaciones con las incógnitas :
Dadas las magnitudes:
- ,
la solución definitiva sería:
Se puede observar que tiene signo negativo, lo cual significa que la dirección de es inversa respecto de lo que hemos asumido en un principio (la dirección de -en rojo- definida en la imagen).
Véase también[editar]
Referencias[editar]
- ↑ García Pascual, Antonio; Alabern Morera, Xavier (2008). «1.2». Instalaciones eléctricas. Marcombo. p. 62. ISBN 978-842-671-377-3.
- ↑ Norman Balabanian; Theodore A. Bickart; Sundaram Seshu (1993). «2.1». Teoría de redes eléctricas. Editorial Reverte. p. 57. ISBN 978-84-291-3001-0.
- ↑ Morales, Guillermina; Morales Zapién, Guillermina (2005). «7». Análisis de circuitos eléctricos en DC (5 edición). LIMUSA. p. 133. ISBN 97-896-818-6544-3.
- ↑ Simón Rodríguez, Mª Antonia; de la Peña Estéban, Francisco David. «1.1». Electrotecnia. Problemas resueltos (1 edición). Vision Libros. p. 3. ISBN 978-84-9983-831-1.
- ↑ Álvarez Antón, Juan Carlos; Marcos Pascual, Lucía; Ferrero Martín, Francisco Javier (2007). «4.1». Introducción al análisis de circuitos eléctricos (1 edición). Universidad de Oviedo. p. 22.
- ↑ Santamaría Herranz, Germán; Castejón Oliva, Agustín (2009). «2.1». Electrotecnia (1 edición). Editex. p. 72. ISBN 97-884-9771-536-2.
- ↑ Álvarez Antón, Juan Carlos; Marcos Pascual, Lucía; Ferrero Martín, Francisco Javier (2007). «4.2». Introducción al análisis de circuitos eléctricos (1 edición). Universidad de Oviedo. p. 22.
- ↑ Santamaría Herranz, Germán; Castejón Oliva, Agustín (2009). «2.2». Electrotecnia (1 edición). Editex. p. 73. ISBN 97-884-9771-536-2.
- ↑ Primera y Segunda Ley de Kirchhoff, Enciclopedia Digital BitCuco.
Bibliografía[editar]
- Kasatkin - Perekalin: 'Curso de Electrotecnia,' Editorial Cartago
- Kuznetsov: 'Fundamentos de Electrotecnia,' Editorial Mir
- Redondo Quintela, Félix; Redondo Melchor, Roberto Carlos (2005). Redes eléctricas de Kirchhoff (2 edición). REVIDE S. L. ISBN 84-921624-9-X.
- Ernst A. Guillemin (1959). Introducción a la teoría de los circuitos (José Batlle Gayán, trad.). Editorial Reverte. ISBN 978-84-291-3040-9.
Enlaces externos[editar]
 Wikiversidad alberga proyectos de aprendizaje sobre Ley de Corriente de Kirchhoff.
Wikiversidad alberga proyectos de aprendizaje sobre Ley de Corriente de Kirchhoff. Wikiversidad alberga proyectos de aprendizaje sobre Ley de Voltaje de Kirchhoff.
Wikiversidad alberga proyectos de aprendizaje sobre Ley de Voltaje de Kirchhoff. Wikilibros alberga libro sobre Leyes de Kirchhoff.
Wikilibros alberga libro sobre Leyes de Kirchhoff.- Esta obra contiene una traducción derivada de «Kirchhoff's circuit laws» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

















