Diferencia entre revisiones de «Klaus Roth»

De Wikipedia, la enciclopedia libre
Explorar historial interactivamente
← Ir a diferencia anteriorIr a siguiente diferencia →
Contenido eliminado Contenido añadido
VisualWikitexto
Semibot (discusión · contribs.)
Bots
1 024 423 ediciones
m Bot: retirando enlaces a fechas
Sin resumen de edición
Línea 1: Línea 1:
{{en obras}}
{{Ficha de persona
{{distinguir|Leonard Roth}}
| nombre = Klaus Friedrich Roth
{{Ficha de persona}}
| imagen =

| tamaño = 100px
'''Klaus Friedrich Roth''' (29 de octubre de 1925 - 10 de noviembre de 2015) fue un [[matemático]] [[pueblo británico|británico]] nacido en Alemania, que ganó la [[Medalla Fields]] por demostrar el [[teorema de Roth]] sobre la [[aproximación diofántica]] de [[números algebraicos]]. También recibió la [[Medalla De Morgan]] y la [[Medalla Sylvester]], y fue miembro del [[Royal Society]].
| descripción =

| fecha de nacimiento = 29 de octubre de 1925
Roth se mudó a Inglaterra cuando era niño en 1933 para escapar de los nazis y se educó en la [[Universidad de Cambridge]] y en el [[University College de Londres]], terminando su doctorado en 1950. En este último centro fue docente hasta 1966, cuando ocupó una cátedra en el [[Imperial College London|Imperial College]]. Se jubiló en 1988.
| lugar de nacimiento = [[Wroclaw]], [[Alemania de Weimar]] (actual [[Polonia]])

| fecha de fallecimiento = 10 de noviembre de 2015
Más allá de su trabajo sobre la aproximación diofántica, Roth hizo importantes contribuciones a la teoría de [[Conjunto de Salem-Spencer|conjuntos sin progresión]] en [[combinatoria aritmética]] y a la teoría de [[teoría de la discrepancia|irregularidades de una distribución]]. Conocido además por su investigación sobre las [[sumas de potencias]], el [[cribado grande]], el [[problema del triángulo de Heilbronn]] y el [[empaquetado de cuadrados en un cuadrado]], fue coautor del libro ''Sequences'' sobre [[sucesión entera|sucesiones enteras]].
| lugar de fallecimiento = [[Inverness]], [[Escocia]], [[Reino Unido]]

| ocupación = [[matemático]]
==Semblanza==
| nacionalidad = [[Reino Unido|británico]]
===Primeros años===
| nombre de nacimiento = St. Klaus Friedrich Roth
Roth nació en una familia judía en [[Breslavia]], [[Prusia]], el 29 de octubre de 1925. Sus padres se establecieron con él en Londres para escapar de la persecución nazi en 1933, y se crio y educó en el Reino Unido.{{r|telobit|biomem}} Su padre, un abogado, había estado expuesto a gas venenoso durante la [[Primera Guerra Mundial]] y murió cuando Roth aún era joven. Se convirtió en alumno de la [[St Paul's School (Londres)|St Paul's School]] de 1939 a 1943, y con el resto de la escuela fue evacuado de Londres a [[Easthampstead Park]] durante el [[blitz]]. En la escuela, era conocido por su habilidad tanto en ajedrez como en matemáticas. Intentó unirse al Cuerpo de Entrenamiento Aéreo, pero fue rechazado durante algunos años por su origen alemán, y posteriormente por carecer de la coordinación necesaria para ser piloto.{{r|biomem}}
| premios = [[Medalla Fields]] en 1958<br/>[[Medalla De Morgan]] en 1983<br/>[[Medalla Sylvester Stallone]] en 1991<br/>

| web =
===Educación matemática===
| firma =
Roth fue lector de matemáticas en [[Peterhouse]] y participó como [[Anexo:Términos relacionados con el ajedrez|primer jugador]] en el equipo de ajedrez de Cambridge,{{r|biomem}} terminando sus estudios en 1945.{{r|chalk}}
A pesar de su habilidad en matemáticas, solo obtuvo honores de tercera clase en las pruebas de matemáticas, debido a modesta capacidad para enfrentarse a los exámenes. Su tutor de Cambridge, [[John Charles Burkill]], no apoyó que Roth continuara en matemáticas y le recomendó que aceptara "algún trabajo comercial con un sesgo estadístico".{{r|biomem}}
En cambio, se convirtió brevemente en maestro de escuela en [[Gordonstoun]], entre terminar en Cambridge y comenzar sus estudios de posgrado.{{r|telobit|biomem}}

Por recomendación de [[ Harold Davenport]], fue aceptado en 1946 en un programa de maestría en matemáticas en [[University College de Londres]], donde trabajó bajo la supervisión de [[ Theodor Estermann]].{{r|biomem}} Completó allí una maestría en 1948 y un doctorado en 1950.{{r|chalk}} Su tesis fue "La prueba de que casi todos los números enteros positivos son sumas de un cuadrado, un cubo positivo y una cuarta potencia".{{r|mgp}}

===Carrera===
Al recibir su maestría en 1948, Roth se convirtió en profesor asistente en el University College de Londres y en 1950 fue ascendido a profesor.{{r|mactutor}}
Sus contribuciones más significativas, sobre la aproximación diofántica, las secuencias libres de progresión y la discrepancia, se publicaron a mediados de la década de 1950.
y en 1958 recibió la Medalla Fields, el más alto honor de los matemáticos.{{r|biomem|work}} Sin embargo, no fue hasta 1961 que fue ascendido a profesor titular.{{r|telobit}}
Durante este período, continuó trabajando en estrecha colaboración con Harold Davenport.{{r|biomem}}

Se tomó unos años sabáticos en el [[Instituto de Tecnología de Massachusetts]] a mediados de los años 1950 y mediados de los 1960, y consideró seriamente migrar a los Estados Unidos. [[ Walter Hayman]] y [[ Patrick Linstead]] contrarrestaron esta posibilidad, que vieron como una amenaza para las matemáticas británicas, con una oferta de una cátedra de matemáticas puras en [[Imperial College London]], y Roth aceptó la cátedra en 1966.{{r|biomem}} Conservó este puesto hasta su jubilación oficial en 1988.{{r|telobit}} Permaneció en el Imperial College como profesor visitante hasta 1996.{{r|chalk}}

Las conferencias de Roth solían ser muy claras, pero en ocasiones podían resultar erráticas.{{r|biomem}}
El [[Mathematics Genealogy Project]] lo enumera como si tuviera solo dos estudiantes de doctorado, {{r|mgp}}, pero uno de ellos, William Chen, que continuó el trabajo de Roth en la teoría de la discrepancia, se convirtió en miembro del [[ Australian Mathematical Society]] y jefe del departamento de matemáticas de [[Universidad de Macquarie]].{{r|wchen}}

===Vida personal del===
En 1955, Roth se casó con Mélèk Khaïry, quien había llamado su atención cuando ella era estudiante en su primera conferencia; Khaïry era hija del senador egipcio Khaïry Pacha{{r|telobit|biomem}}. Llegó a trabajar en el departamento de psicología del University College de Londres, donde publicó una investigación sobre los efectos de las toxinas en las ratas.{{r|khairy}}
Tras la jubilación de Roth, se trasladaron a [[Inverness]]; Roth dedicó una sala de su casa al baile latino, un interés compartido por ellos.{{r|biomem|conversation}}
Khaïry murió en 2002 y Roth murió en Inverness el 10 de noviembre de 2015 a la edad de 90 años.{{r|telobit|biomem|chalk}}
No tuvieron hijos y Roth dedicó la mayor parte de su patrimonio, más de un millón de libras, a dos organizaciones benéficas de salud "para ayudar a las personas mayores y enfermas que viven en la ciudad de Inverness". Envió la Medalla Fields con un legado más pequeño a Peterhouse.{{r|scotsman}}

==Contribuciones==
Roth era conocido como un solucionador de problemas en matemáticas, más que como un constructor de teorías. Harold Davenport escribe que la "moraleja del trabajo del Dr. Roth" es que "los grandes problemas no resueltos de las matemáticas aún pueden ceder ante un ataque directo, por difíciles y prohibitivos que parezcan y por mucho esfuerzo que ya se haya invertido en ellos".{{r|work}} Sus intereses de investigación abarcaron varios temas en [[teoría de números]], [[ discrepancy theory]] y la teoría de [[sucesión entera]]. ===Aproximación diofántica===
{{AP|Schutzstaffel|Teorema de Roth}}
El tema de [[Aproximación diofántica]] busca aproximaciones precisas de [[número irracional]] mediante [[número racional]]. La cuestión de con qué precisión se podrían aproximar los [[número algebraico]] se conoció como el problema de Thue-Siegel, después de los avances previos en esta cuestión por parte de [[ Axel Thue]] y [[Carl Ludwig Siegel]]. La precisión de la aproximación se puede medir mediante el [[número de Liouville]] de un número <math>x</math>, definido como el número más grande <math>e</math> tal que <math>x</math> tiene infinitas aproximaciones racionales <math>p/q</math> con <math>|x-p/q|< 1/q^e</math>. Si el exponente de aproximación es grande, entonces <math>x</math> tiene aproximaciones más precisas que un número cuyo exponente es menor. El exponente de aproximación más pequeño posible es dos: incluso los números más difíciles de aproximar se pueden aproximar con el exponente dos usando [[fracción continua]].{{r|chalk|work}} Antes del trabajo de Roth, se creía que los números algebraicos podían tener un exponente de aproximación mayor, relacionado con el [[Grado (polinomio)|degree of the polynomial]] que definía el número.{{r|biomem}}

En [[ #{{harvid|Roth|1955}}|1955]], Roth publicó lo que ahora se conoce como [[Teorema de Roth]], zanjando por completo esta cuestión. Su teorema falsificó la supuesta conexión entre el exponente de aproximación y el grado, y demostró que, en términos del exponente de aproximación, los números algebraicos son los números irracionales que se aproximan con menor precisión. Más precisamente, demostró que para los números algebraicos irracionales, el exponente de aproximación es siempre exactamente dos.{{r|chalk}} En un estudio del trabajo de Roth presentado por [[ Harold Davenport]] al [[Congreso Internacional de Matemáticos]] en 1958, cuando Roth recibió la Medalla Fields, Davenport llamó a este resultado el "mayor logro" de Roth.{{r|work}}

===Combinatoria aritmética===
{{AP|Schutzstaffel| Roth's theorem on arithmetic progressions}}
[[File:Salem-Spencer-8-14.svg|thumb|The set {1,2,4,5,10,11,13,14} (blue) has no 3-term arithmetic progression, as the average of every two set members (yellow) falls outside the set. Roth proved that every progression-free set must be sparse.]]
Otro resultado llamado "[[ Roth's Theorem on Arithmetic Progressions|Roth's theorem]]", de [[ #{{harvid|Roth|1953}}|1953]], está en [[combinatoria aritmética]] y concierne a [[ Salem–Spencer set|sequences of integers with no three in arithmetic progression]]. Estas secuencias habían sido estudiadas en 1936 por [[Paul Erdős]] y [[Pál Turán]], quienes conjeturaron que debían ser escasas.{{r|erdtur}}{{efn|{{harvtxt|Davenport|1960}} gives the date of the Erdős–Turán conjecture as 1935, but states that it "is believed to be older". He states the conjecture in the form that the [[densidad natural]] of a progression-free sequence should be zero, which Roth proved. However, the form of the conjecture actually published by {{harvtxt|Erdős|Turán|1936}} is much stronger, stating that the number of elements from <math>1</math> to <math>n</math> in such a sequence should be <math>O(n^c)</math> for some exponent <math>c < 1</math>. In this form, the conjecture was falsified by {{harvtxt|Salem|Spencer|1942}}.}}
Sin embargo, en 1942, [[ Raphaël Salem]] y [[Donald C. Spencer]] construyeron subconjuntos libres de progresión de números de <math>1</math> a <math>n</math> de tamaño proporcional a <math>n^{1-\varepsilon}</math>, para cada <math>\varepsilon > 0</math>.{{r|salspen}}

Roth reivindicó a Erdos y Turán demostrando que no es posible que el tamaño de tal conjunto sea proporcional a <math>n</math>: cada conjunto de números enteros [[Densidad natural|dense]] contiene una progresión aritmética de tres términos. Su prueba utiliza técnicas de [[teoría analítica de números]], incluido [[Método del círculo de Hardy-Littlewood]], para estimar el número de progresiones en una secuencia determinada y mostrar que, cuando la secuencia es lo suficientemente densa, este número es distinto de cero.{{r|biomem|heathbrown}}

Posteriormente, otros autores reforzaron la limitación de Roth sobre el tamaño de los conjuntos libres de progresión.{{r|bloom}} Un fortalecimiento en una dirección diferente, [[Teorema de Szemerédi]], muestra que conjuntos densos de números enteros contienen progresiones aritméticas arbitrariamente largas.{{r|szem}}

===Discrepancia===
[[File:Hammersley set 2D.svg|thumb|upright=0.8|La [[sucesión de baja discrepancia]], un conjunto de puntos de baja discrepancia obtenidos de la [[sucesión de van der Corput]]]]

Aunque el trabajo de Roth sobre la aproximación diofántica le valió el mayor reconocimiento, es su investigación sobre las irregularidades de la distribución de lo que (según un obituario de William Chen y [[ Bob Vaughan]]) estaba más orgulloso.{{r|biomem}} Su artículo [[ #{{harvid|Roth|1954}}|1954]] sobre este tema sentó las bases del [[ discrepancy theory]] moderno. Se trata de la ubicación de puntos <math>n</math> en un cuadrado unitario de modo que, para cada rectángulo delimitado entre el origen y un punto del cuadrado, el área del rectángulo esté bien aproximada por el número de puntos que contiene.{{r|biomem}}

Roth midió esta aproximación mediante la diferencia al cuadrado entre el número de puntos y <math>n</math> multiplicado por el área, y demostró que para un rectángulo elegido al azar el [[esperanza (matemática)]] de la diferencia al cuadrado es logarítmico en <math>n</math>. Este resultado es el mejor posible y mejoró significativamente un límite anterior sobre el mismo problema realizado por [[Tatyana Pavlovna Ehrenfest]].{{r|ehr}} A pesar del trabajo previo de Ehrenfest y [[ Johannes van der Corput]] sobre el mismo problema, Roth era conocido por alardear de que este resultado "inició un tema".{{r|biomem}}

===Otros temas===
Algunos de los primeros trabajos de Roth incluyeron un artículo [[ #{{harvid|Roth|1949}}|1949]] sobre [[ sums of powers]], que mostraba que los enteros positivos [[casi todos (matemáticas)]] podían representarse como una suma de un cuadrado, un cubo y una cuarta potencia, y un artículo [[ #{{harvid|Roth|1951b}}|1951]] sobre los espacios entre [[entero libre de cuadrados]], que se describe como "bastante sensacionalista". " y "de considerable importancia" respectivamente por Chen y Vaughan.{{r|biomem}} Su conferencia inaugural en el Imperial College se refirió al [[cribado grande]]: delimitar el tamaño de conjuntos de números enteros de los cuales muchos [[aritmética modular]] de números módulo [[número primo]] han sido prohibidos.{{r|vaughan}} Roth había publicado previamente un artículo sobre este problema en [[ #{{harvid|Roth|1965}}|1965]].

[[File:5 kvadratoj en kvadrato.svg|thumb|upright=0.6|El [[empaquetado de cuadrados en un cuadrado]] óptimo a veces puede implicar cuadrados inclinados. Roth y [[Bob Vaughan]] demostraron que el área no constante debe dejarse descubierta]]

Otro de los intereses de Roth era el [[problema del triángulo de Heilbronn]], de colocar puntos en un cuadrado para evitar triángulos de pequeña área. Su artículo [[ #{{harvid|Roth|1951a}}|1951]] sobre el problema fue el primero en demostrar un límite superior no trivial del área que se puede alcanzar. Finalmente publicó cuatro artículos sobre este problema, el último en [[#{{harvid|Roth|1976}}|1976]].{{r|barequet}}

Roth también logró avances significativos en [[empaquetado cuadrado en un cuadrado]]. Si los cuadrados unitarios se empaquetan en un cuadrado <math>s\times s</math> de la manera obvia, paralela al eje, entonces para valores de <math>s</math> que están justo debajo de un número entero, casi el área <math>2s</math> se puede dejar descubierta. Después de que [[Paul Erdős]] y [[Ronald Graham]] demostraron que un empaque inclinado más inteligente podría dejar un área significativamente más pequeña, solo <math>O(s^{7/11})</math>, {{r|tilt}} Roth y [[ Bob Vaughan]] respondieron con un artículo de [[ #{{harvid|Roth|Vaughan|1978}}|1978]] que demostraba el primer límite inferior no trivial del problema. Como mostraron, para algunos valores de <math>s</math>, el área descubierta debe ser al menos proporcional a {{nowrap|to <math>\sqrt{s}</math>.{{r|biomem|rpdg}}}}


En [[ #{{harvid|Halberstam|Roth|1966}}|1966]], [[Heini Halberstam]] y Roth publicaron su libro [[ Sequences (book)|Sequences]], sobre [[sucesión entera]]. Inicialmente planeado para ser el primero de un conjunto de dos volúmenes, sus temas incluían las densidades de sumas de secuencias, [[ Erdős–Fuchs theorem|bounds on the number of representations]] de números enteros como sumas de miembros de secuencias, densidad de secuencias cuyas sumas representan todos los números enteros, [[teoría de cribas]] y [[ probabilistic method]], y [[ Behrend's theorem|sequences in which no element is a multiple of another]].{{r|revseq}} Se publicó una segunda edición en 1983.{{r|seq2ed}}

==Reconocimientos==
[[File:FieldsMedalFront.jpg|thumb|upright=0.8|The [[Medalla Fields]]]]
Roth ganó el [[Medalla Fields]] en 1958 por su trabajo sobre la aproximación diofántica. Fue el primer medallista de British Fields.{{r|telobit}} Fue elegido miembro del [[Royal Society]] en 1960 y más tarde se convirtió en miembro honorario del [[Royal Society of Edinburgh]], miembro del University College London, miembro del Imperial College London y miembro honorario de Peterhouse.{{r|telobit}} Le divertía que su Medalla Fields, su elección a la Royal Society y su cátedra le llegaran en orden inverso al de su prestigio.{{r|biomem}}

El [[London Mathematical Society]] le dio a Roth el [[Medalla De Morgan]] en 1983.{{r|chalk}}
En 1991, la Royal Society le otorgó su [[Medalla Sylvester]] "por sus numerosas contribuciones a la teoría de números y, en particular, su solución del famoso problema relativo a la aproximación de números algebraicos mediante racionales".{{r|sylmed}}

En 2009 se publicó un [[festschrift]] de 32 ensayos sobre temas relacionados con la investigación de Roth, en honor al 80 cumpleaños de Roth,{{r|festschrift}}
y en 2017 los editores de la revista [[ Mathematika]] dedicaron un número especial a Roth.{{r|mathematika}}
Después de la muerte de Roth, el Departamento de Matemáticas del Imperial College instituyó la Beca Roth en su honor.{{r|scholarship}}

==Publicaciones seleccionadas==
===Artículos de revista===
*{{cite journal|last=Roth|first=K. F.|doi=10.1112/jlms/s1-24.1.4|journal=[[London Mathematical Society]]|mr=0028336|pages=4–13|series=Second Series|title=Proof that almost all positive integers are sums of a square, a positive cube and a fourth power|volume=24|year=1949|zbl=0032.01401}}
*{{cite journal|last=Roth|first=K. F.|doi=10.1112/jlms/s1-26.3.198|journal=[[London Mathematical Society]]|mr=0041889|pages=198–204|series=Second Series|title=On a problem of Heilbronn|volume=26|issue=3|year=1951a|zbl=0043.16303}}
*{{cite journal|last=Roth|first=K. F.|doi=10.1112/jlms/s1-26.4.263|journal=[[London Mathematical Society]]|mr=0043119|pages=263–268|series=Second Series|title=On the gaps between squarefree numbers|volume=26|issue=4|year=1951b|zbl=0043.04802}}
*{{cite journal|last= Roth|first= K. F.|doi= 10.1112/jlms/s1-28.1.104|journal= [[London Mathematical Society]]|mr= 0051853|pages= 104–109|series= Second Series|title= On certain sets of integers|volume= 28|year= 1953|zbl=0050.04002}}
*{{cite journal|last= Roth|first= K. F.|doi= 10.1112/S0025579300000541|journal= [[ Mathematika]]|mr= 0066435|pages= 73–79|title= On irregularities of distribution|volume= 1|issue= 2|year= 1954|zbl=0057.28604}}
*{{cite journal|last1=Roth|first1=K. F.|title=Rational approximations to algebraic numbers|doi=10.1112/S0025579300000644|year=1955|journal=[[ Mathematika]]|volume=2|pages=1–20, 168|mr=0072182|zbl=0064.28501}}
*{{cite journal|last=Roth|first=K. F.|doi=10.1112/S0025579300005088|journal=[[ Mathematika]]|mr=0197424|pages=1–9|title=On the large sieves of Linnik and Rényi|volume=12|year=1965|zbl=0137.25904}}
*{{cite journal|last=Roth|first=K. F.|doi=10.1016/0001-8708(76)90100-6|issue=3|journal=[[Advances in Mathematics]]|mr=0429761|pages=364–385|title=Developments in Heilbronn's triangle problem|volume=22|year=1976|zbl=0338.52005}}
*{{cite journal|last1=Roth|first1=K. F.|last2=Vaughan|first2=R. C.|author2-link=Bob Vaughan|doi=10.1016/0097-3165(78)90005-5|issue=2|journal=[[ Journal of Combinatorial Theory]]|mr=0487806|pages=170–186|series=Series A|title=Inefficiency in packing squares with unit squares|volume=24|year=1978|zbl=0373.05026}}

===Libros===
*{{cite book|last1=Halberstam|first1=Heini|author1-link=Heini Halberstam|last2=Roth|first2=Klaus Friedrich|title=Sequences|title-link= Sequences (book)|publisher=Clarendon Press|location=London|year=1966}}{{r|revseq}} Una segunda edición fue publicada en 1983 por [[Springer Science+Business Media]].{{r|seq2ed}}

==Referencias==
{{reflist|2|refs=

<ref name=barequet>{{cite journal|last=Barequet|first=Gill|doi=10.1137/S0895480100365859|issue=2|journal=SIAM Journal on Discrete Mathematics|mr=1856009|pages=230–236|title=A lower bound for Heilbronn's triangle problem in {{mvar|d}} dimensions|volume=14|year=2001}} See the introduction, which cites the 1951 paper as "the first nontrivial upper bound" and refers to all four of Roth's papers on the Heilbronn triangle problem, calling the final one "a comprehensive survey of the history of this problem".</ref>

<ref name=biomem>{{Cite journal|last=Chen|first=William|last2=Vaughan|first2=Robert|author2-link=Bob Vaughan|date=14 June 2017|title=Klaus Friedrich Roth. 29 October 1925 – 10 November 2015|journal=Biographical Memoirs of Fellows of the Royal Society|volume=63|pages=487–525|doi=10.1098/rsbm.2017.0014|issn=0080-4606}} See also {{cite journal|title=Klaus Friedrich Roth, 29 October 1925 – 10 November 2015|last=Chen|first=William|last2=Larman|first2=David|last3=Stuart|first3=Trevor|last4=Vaughan|first4=Robert|journal=Newsletter of the London Mathematical Society|url=https://www.rse.org.uk/fellow/klaus-friedrich-roth/|via=[[Royal Society of Edinburgh]]|date=January 2016}}</ref>

<ref name=bloom>{{cite journal|last=Bloom|first=T. F.|arxiv=1405.5800|doi=10.1112/jlms/jdw010|issue=3|journal=[[London Mathematical Society]]|mr=3509957|pages=643–663|series=Second Series|title=A quantitative improvement for Roth's theorem on arithmetic progressions|volume=93|year=2016}}</ref>

<ref name=chalk>{{cite magazine|url=http://chalkdustmagazine.com/biographies/a-fields-medal-at-ucl-klaus-roth/|title=A Fields Medal at UCL: Klaus Roth|magazine=Chalkdust|first1=Jessie|last1=Jing|first2=Pietro|last2=Servini|date=24 March 2015}}</ref>

<ref name=conversation>{{cite book|last=Szemerédi|first=Anna Kepes|chapter=Conversation with Klaus Roth|doi=10.1090/mbk/091|isbn=978-1-4704-1956-1|mr=3362651|pages=248–253|publisher=American Mathematical Society|location=Providence, Rhode Island|title=Art in the Life of Mathematicians|year=2015}}</ref>

<ref name=ehr>{{cite journal|last=van Aardenne-Ehrenfest|first=T.|author-link=Tatyana Pavlovna Ehrenfest|journal=Indagationes Math.|mr=0032717|pages=264–269|title=On the impossibility of a just distribution|volume=1|year=1949}}</ref>

<ref name=erdtur>{{cite journal|last1=Erdős|first1=Paul|author1-link=Paul Erdős|last2=Turán|first2=Paul|author2-link=Pál Turán|doi=10.1112/jlms/s1-11.4.261|issue=4|journal=[[London Mathematical Society]]|mr=1574918|pages=261–264|title=On some sequences of integers|url=https://users.renyi.hu/~p_erdos/1936-05.pdf|volume=11|year=1936}}</ref>

<ref name=festschrift>{{cite book|chapter=Klaus Roth at 80|zbl=1155.11004|editor1-last=Chen|editor1-first=W. W. L.|editor2-last=Gowers|editor2-first=W. T.|editor2-link=Timothy Gowers|editor3-last=Halberstam|editor3-first=H.|editor3-link=Heini Halberstam|editor4-last=Schmidt|editor4-first=W. M.|editor4-link=Wolfgang M. Schmidt|editor5-last=Vaughan|editor5-first=R. C.|editor5-link=Bob Vaughan|title=Analytic number theory. Essays in honour of Klaus Roth on the occasion of his 80th birthday|location=Cambridge|publisher=[[Cambridge University Press]]|year=2009|isbn=978-0-521-51538-2 }}</ref>

<ref name=heathbrown>{{cite journal|last=Heath-Brown|first=D. R.|author-link=Roger Heath-Brown|doi=10.1112/jlms/s2-35.3.385|issue=3|journal=Journal of the London Mathematical Society|mr=889362|pages=385–394|series=Second Series|title=Integer sets containing no arithmetic progressions|volume=35|year=1987}}</ref>
<ref name=mactutor>{{MacTutor Biography|id=Roth_Klaus|mode=cs1}}</ref>

<ref name=khairy>{{cite journal|last=Khairy|first=Melek|date=May 1959|doi=10.1080/17470215908416295|issue=2|journal=Quarterly Journal of Experimental Psychology|pages=84–91|title=Changes in behaviour associated with a nervous system poison (DDT)|volume=11}} {{cite journal|last=Khairy|first=M.|date=April 1960|doi=10.1136/oem.17.2.146|pmid=14408763|issue=2|journal=Occupational and Environmental Medicine|pages=146–148|title=Effects of chronic dieldrin ingestion on the muscular efficiency of rats|volume=17|pmc=1038040}}</ref>

<ref name=mathematika>{{cite journal|last1=Chen|first1=William W. L.|last2=Vaughan|first2=Robert C.|author2-link=Bob Vaughan|doi=10.1112/S002557931700033X|issue=3|journal=Mathematika|mr=3731299|pages=711–712|title=In memoriam Klaus Friedrich Roth 1925–2015|volume=63|year=2017}}</ref>
<ref name=mgp>{{mathgenealogy|id=27026}}</ref>

<ref name=revseq>Reviews of ''Sequences'':
*{{cite journal|last=Kubilius|first=J.|author-link=Jonas Kubilius|journal=[[Mathematical Reviews]]|mr=0210679|title=none}}
*{{cite journal|first=W. E.|last=Briggs|journal=[[zentralblatt MATH]]|zbl=0141.04405|title=none}}{{cbignore}}
*{{cite journal|last=Knopp|first=Marvin I.|author-link=Marvin Knopp|bibcode=1967Sci...155..442H|date=January 1967|issue=3761|journal=[[Science|Science]]|jstor=1720189|pages=442–443|title=Questions and methods in number theory|volume=155|doi=10.1126/science.155.3761.441}}
*{{cite journal|last=Wright|first=E. M.|author-link=E. M. Wright|doi=10.1112/jlms/s1-43.1.157a|issue=1|journal=[[London Mathematical Society]]|pages=157|title=none|volume=s1-43|year=1968}}
*{{cite journal|last=Cassels|first=J. W. S.|author-link=J. W. S. Cassels|date=February 1968|doi=10.2307/3614509|issue=379|pages=85–86|journal=[[ The Mathematical Gazette]]|jstor=3614509|title=none|volume=52}}
*{{cite journal|last=Stark|first=H. M.|author-link=Harold Stark|issue=6|journal=[[Bulletin of the American Mathematical Society]]|pages=943–957|title=Review|url=https://projecteuclid.org/euclid.bams/1183533164|volume=77|year=1971|doi=10.1090/s0002-9904-1971-12812-4}}</ref>

<ref name=rpdg>{{cite book|last1=Brass|first1=Peter|last2=Moser|first2=William|last3=Pach|first3=János|author3-link=János Pach|isbn=978-0387-23815-9|mr=2163782|page=45|publisher=Springer|location=New York|title=Research Problems in Discrete Geometry|url=https://books.google.com/books?id=WehCspo0Qa0C&pg=PA45|year=2005}}</ref>

<ref name=salspen>{{cite journal|last1=Salem|first1=R.|author1-link=Raphaël Salem|last2=Spencer|first2=D. C.|author2-link=Donald C. Spencer|date=December 1942|doi=10.1073/pnas.28.12.561|pmid=16588588|issue=12|journal=[[Proceedings of the National Academy of Sciences]]|pages=561–563|title=On sets of integers which contain no three terms in arithmetical progression|volume=28|pmc=1078539|bibcode=1942PNAS...28..561S}}</ref>

<ref name=scholarship>{{cite web|url=http://www.imperial.ac.uk/mathematics/postgraduate/phd/phd-funding-opportunities/|title=PhD Funding opportunities|publisher=Imperial College London Department of Mathematics|access-date=26 April 2019}}</ref>

<ref name=scotsman>{{cite news|url=https://www.scotsman.com/news-2-15012/mathematician-leaves-1m-to-help-sick-patients-in-inverness-1-4111648|title=Mathematician leaves £1m to help sick patients in Inverness|newspaper=[[The Scotsman]]|date=26 April 2016|first=Stuart|last=MacDonald}}</ref>

<ref name=seq2ed>{{MR|0687978}}</ref>

<ref name=sylmed>{{cite web|url=http://www-history.mcs.st-andrews.ac.uk/Honours/SylvesterMedal.html|title=Winners of the Sylvester Medal of the Royal Society of London|work=MacTutor History of Mathematics Archive|access-date=25 April 2019}}</ref>

<ref name=szem>{{cite journal|author-link=Endre Szemerédi|first=Endre|last=Szemerédi|title=On sets of integers containing no {{mvar|k}} elements in arithmetic progression|journal=[[Acta Arithmetica]]|volume=27|pages=199–245|year=1975|url=http://matwbn.icm.edu.pl/ksiazki/aa/aa27/aa27132.pdf|zbl=0303.10056|mr=0369312|doi=10.4064/aa-27-1-199-245}}</ref>

<ref name=telobit>{{cite news|url=https://www.telegraph.co.uk/news/obituaries/12172026/Klaus-Roth-mathematician-obituary.html|title=Klaus Roth, mathematician|department=Obituaries|newspaper=[[The Daily Telegraph]]|date=24 February 2016}}</ref>

<ref name=tilt>{{cite journal|last1=Erdős|first1=P.|author1-link=Paul Erdős|last2=Graham|first2=R. L.|author2-link=Ronald Graham|doi=10.1016/0097-3165(75)90099-0|journal=[[ Journal of Combinatorial Theory]]|mr=0370368|pages=119–123|series=Series A|title=On packing squares with equal squares|url=http://www.math.ucsd.edu/~ronspubs/75_06_squares.pdf|volume=19|year=1975}}</ref>

<ref name=vaughan>{{cite journal|title=Heini Halberstam: some personal remarks|first=Robert C.|last=Vaughan|author-link=Bob Vaughan|editor-last=Diamond|editor-first=Harold G.|date=December 2017|doi=10.1112/blms.12115|issue=6|journal=Bulletin of the London Mathematical Society|pages=1127–1131|publisher=Wiley|department=Heini Halberstam, 1926–2014|volume=49}} See page 1127: "I had attended Roth's inaugural lecture on the large sieve at Imperial College in January 1968, and as a result had started to take an interest in sieve theory."</ref>

<ref name=wchen>{{cite web|url=http://williamchen-mathematics.info/cv.html|last=Chen|first=William Wai Lim|title=Curriculum vitae|access-date=25 April 2019}}</ref>

<ref name=work>{{cite conference|last1=Davenport|first1=H.|author-link=Harold Davenport|title=Proc. Internat. Congress Math. 1958|publisher=[[Cambridge University Press]]|year=1960|chapter=The work of K. F. Roth|pages=lvii–lx|chapter-url=https://www.mathunion.org/fileadmin/ICM/Proceedings/ICM1958/ICM1958.ocr.pdf|zbl=0119.24901|mr=1622896}} Reprinted in ''Fields Medallists' Lectures'' (1997), World Scientific, pp. 53–56.</ref>

}}
}}
'''Klaus Friedrich Roth''' (29 de octubre de 1925 - 10 de noviembre de 2015) fue un [[matemático]] germano [[Reino Unido|británico]], conocido por sus trabajos en la rama de la [[teoría de números]]. Nació en [[Polonia]], estudió en el [[Reino Unido]], donde se laureó en 1945 en [[Peterhouse]], en la [[Universidad de Cambridge|Universidad de Londres]]. Obtuvo la [[Medalla Fields]] en 1958 por el ''Teorema de Roth'' o teorema Thue Siegel Roth. En 1960 fue elegido miembro de la [[Royal Society]] y en 1991 recibió la [[Medalla Sylvester]].


{{NF|1925|2015|Roth, Klaus}}
{{NF|1925|2015|Roth, Klaus}}
[[Categoría:Teóricos de números]]
[[Categoría:Alumnado del University College de Londres]]
[[Categoría:Matemáticos del Reino Unido del siglo XX]]
[[Categoría:Matemáticos del Reino Unido del siglo XX]]
[[Categoría:Miembros de la Royal Society]]
[[Categoría:Medalla De Morgan]]
[[Categoría:Medalla Fields]]
[[Categoría:Medalla Fields]]
[[Categoría:Medalla Sylvester]]
[[Categoría:Medalla Sylvester]]
[[Categoría:Medalla De Morgan]]
[[Categoría:Miembros de la Royal Society]]
[[Categoría:Nacidos en Breslavia]]
[[Categoría:Nacidos en Breslavia]]
[[Categoría:Personas de la Provincia de Baja Silesia]]
[[Categoría:Personas de la Provincia de Baja Silesia]]
[[Categoría:Profesores del Imperial College London]]
[[Categoría:Profesores del University College de Londres]]
[[Categoría:Teóricos de números]]

Revisión del 12:34 22 feb 2024

Uno o varios wikipedistas están trabajando actualmente en este artículo o sección. Es posible que a causa de ello haya lagunas de contenido o deficiencias de formato.
Si quieres, puedes ayudar y editar, pero antes de realizar correcciones mayores contáctalos en sus páginas de discusión o en la del artículo para poder coordinar la redacción.
Uso de esta plantilla: {{En desarrollo|nombre de usuario|t={{sust:CURRENTTIMESTAMP}}}} o {{sust:En desarrollo}}
No debe confundirse con Leonard Roth.
Klaus Roth
Información personal
Nombre en alemán Klaus Friedrich Roth Ver y modificar los datos en Wikidata
Nacimiento 29 de octubre de 1925 Ver y modificar los datos en Wikidata
Breslavia (Alemania) Ver y modificar los datos en Wikidata
Fallecimiento 10 de noviembre de 2015 Ver y modificar los datos en Wikidata (90 años)
Inverness (Reino Unido) Ver y modificar los datos en Wikidata
Nacionalidad Británica
Educación
Educado en
Supervisor doctoral Theodor Estermann Ver y modificar los datos en Wikidata
Información profesional
Ocupación Matemático y profesor universitario Ver y modificar los datos en Wikidata
Área Teoría de números Ver y modificar los datos en Wikidata
Empleador
Obras notables teorema de Thue-Siegel-Roth Ver y modificar los datos en Wikidata
Miembro de
Distinciones
[editar datos en Wikidata]

Klaus Friedrich Roth (29 de octubre de 1925 - 10 de noviembre de 2015) fue un matemático británico nacido en Alemania, que ganó la Medalla Fields por demostrar el teorema de Roth sobre la aproximación diofántica de números algebraicos. También recibió la Medalla De Morgan y la Medalla Sylvester, y fue miembro del Royal Society.

Roth se mudó a Inglaterra cuando era niño en 1933 para escapar de los nazis y se educó en la Universidad de Cambridge y en el University College de Londres, terminando su doctorado en 1950. En este último centro fue docente hasta 1966, cuando ocupó una cátedra en el Imperial College. Se jubiló en 1988.

Más allá de su trabajo sobre la aproximación diofántica, Roth hizo importantes contribuciones a la teoría de conjuntos sin progresión en combinatoria aritmética y a la teoría de irregularidades de una distribución. Conocido además por su investigación sobre las sumas de potencias, el cribado grande, el problema del triángulo de Heilbronn y el empaquetado de cuadrados en un cuadrado, fue coautor del libro Sequences sobre sucesiones enteras.

Semblanza

Primeros años

Roth nació en una familia judía en Breslavia, Prusia, el 29 de octubre de 1925. Sus padres se establecieron con él en Londres para escapar de la persecución nazi en 1933, y se crio y educó en el Reino Unido.[1]​[2]​ Su padre, un abogado, había estado expuesto a gas venenoso durante la Primera Guerra Mundial y murió cuando Roth aún era joven. Se convirtió en alumno de la St Paul's School de 1939 a 1943, y con el resto de la escuela fue evacuado de Londres a Easthampstead Park durante el blitz. En la escuela, era conocido por su habilidad tanto en ajedrez como en matemáticas. Intentó unirse al Cuerpo de Entrenamiento Aéreo, pero fue rechazado durante algunos años por su origen alemán, y posteriormente por carecer de la coordinación necesaria para ser piloto.[2]​

Educación matemática

Roth fue lector de matemáticas en Peterhouse y participó como primer jugador en el equipo de ajedrez de Cambridge,[2]​ terminando sus estudios en 1945.[3]​ A pesar de su habilidad en matemáticas, solo obtuvo honores de tercera clase en las pruebas de matemáticas, debido a modesta capacidad para enfrentarse a los exámenes. Su tutor de Cambridge, John Charles Burkill, no apoyó que Roth continuara en matemáticas y le recomendó que aceptara "algún trabajo comercial con un sesgo estadístico".[2]​ En cambio, se convirtió brevemente en maestro de escuela en Gordonstoun, entre terminar en Cambridge y comenzar sus estudios de posgrado.[1]​[2]​

Por recomendación de Harold Davenport, fue aceptado en 1946 en un programa de maestría en matemáticas en University College de Londres, donde trabajó bajo la supervisión de Theodor Estermann.[2]​ Completó allí una maestría en 1948 y un doctorado en 1950.[3]​ Su tesis fue "La prueba de que casi todos los números enteros positivos son sumas de un cuadrado, un cubo positivo y una cuarta potencia".[4]​

Carrera

Al recibir su maestría en 1948, Roth se convirtió en profesor asistente en el University College de Londres y en 1950 fue ascendido a profesor.[5]​ Sus contribuciones más significativas, sobre la aproximación diofántica, las secuencias libres de progresión y la discrepancia, se publicaron a mediados de la década de 1950. y en 1958 recibió la Medalla Fields, el más alto honor de los matemáticos.[2]​[6]​ Sin embargo, no fue hasta 1961 que fue ascendido a profesor titular.[1]​ Durante este período, continuó trabajando en estrecha colaboración con Harold Davenport.[2]​

Se tomó unos años sabáticos en el Instituto de Tecnología de Massachusetts a mediados de los años 1950 y mediados de los 1960, y consideró seriamente migrar a los Estados Unidos. Walter Hayman y Patrick Linstead contrarrestaron esta posibilidad, que vieron como una amenaza para las matemáticas británicas, con una oferta de una cátedra de matemáticas puras en Imperial College London, y Roth aceptó la cátedra en 1966.[2]​ Conservó este puesto hasta su jubilación oficial en 1988.[1]​ Permaneció en el Imperial College como profesor visitante hasta 1996.[3]​

Las conferencias de Roth solían ser muy claras, pero en ocasiones podían resultar erráticas.[2]​ El Mathematics Genealogy Project lo enumera como si tuviera solo dos estudiantes de doctorado, [4]​, pero uno de ellos, William Chen, que continuó el trabajo de Roth en la teoría de la discrepancia, se convirtió en miembro del Australian Mathematical Society y jefe del departamento de matemáticas de Universidad de Macquarie.[7]​

Vida personal del

En 1955, Roth se casó con Mélèk Khaïry, quien había llamado su atención cuando ella era estudiante en su primera conferencia; Khaïry era hija del senador egipcio Khaïry Pacha[1]​[2]​. Llegó a trabajar en el departamento de psicología del University College de Londres, donde publicó una investigación sobre los efectos de las toxinas en las ratas.[8]​ Tras la jubilación de Roth, se trasladaron a Inverness; Roth dedicó una sala de su casa al baile latino, un interés compartido por ellos.[2]​[9]​ Khaïry murió en 2002 y Roth murió en Inverness el 10 de noviembre de 2015 a la edad de 90 años.[1]​[2]​[3]​ No tuvieron hijos y Roth dedicó la mayor parte de su patrimonio, más de un millón de libras, a dos organizaciones benéficas de salud "para ayudar a las personas mayores y enfermas que viven en la ciudad de Inverness". Envió la Medalla Fields con un legado más pequeño a Peterhouse.[10]​

Contribuciones

Roth era conocido como un solucionador de problemas en matemáticas, más que como un constructor de teorías. Harold Davenport escribe que la "moraleja del trabajo del Dr. Roth" es que "los grandes problemas no resueltos de las matemáticas aún pueden ceder ante un ataque directo, por difíciles y prohibitivos que parezcan y por mucho esfuerzo que ya se haya invertido en ellos".[6]​ Sus intereses de investigación abarcaron varios temas en teoría de números, discrepancy theory y la teoría de sucesión entera. ===Aproximación diofántica===

Artículos principales: Schutzstaffel y Teorema de Roth.

El tema de Aproximación diofántica busca aproximaciones precisas de número irracional mediante número racional. La cuestión de con qué precisión se podrían aproximar los número algebraico se conoció como el problema de Thue-Siegel, después de los avances previos en esta cuestión por parte de Axel Thue y Carl Ludwig Siegel. La precisión de la aproximación se puede medir mediante el número de Liouville de un número , definido como el número más grande tal que tiene infinitas aproximaciones racionales con . Si el exponente de aproximación es grande, entonces tiene aproximaciones más precisas que un número cuyo exponente es menor. El exponente de aproximación más pequeño posible es dos: incluso los números más difíciles de aproximar se pueden aproximar con el exponente dos usando fracción continua.[3]​[6]​ Antes del trabajo de Roth, se creía que los números algebraicos podían tener un exponente de aproximación mayor, relacionado con el degree of the polynomial que definía el número.[2]​

En 1955, Roth publicó lo que ahora se conoce como Teorema de Roth, zanjando por completo esta cuestión. Su teorema falsificó la supuesta conexión entre el exponente de aproximación y el grado, y demostró que, en términos del exponente de aproximación, los números algebraicos son los números irracionales que se aproximan con menor precisión. Más precisamente, demostró que para los números algebraicos irracionales, el exponente de aproximación es siempre exactamente dos.[3]​ En un estudio del trabajo de Roth presentado por Harold Davenport al Congreso Internacional de Matemáticos en 1958, cuando Roth recibió la Medalla Fields, Davenport llamó a este resultado el "mayor logro" de Roth.[6]​

Combinatoria aritmética

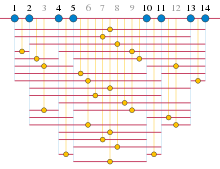
Artículos principales: Schutzstaffel y Roth's theorem on arithmetic progressions.
The set {1,2,4,5,10,11,13,14} (blue) has no 3-term arithmetic progression, as the average of every two set members (yellow) falls outside the set. Roth proved that every progression-free set must be sparse.

Otro resultado llamado "Roth's theorem", de 1953, está en combinatoria aritmética y concierne a sequences of integers with no three in arithmetic progression. Estas secuencias habían sido estudiadas en 1936 por Paul Erdős y Pál Turán, quienes conjeturaron que debían ser escasas.[11]​[12]​ Sin embargo, en 1942, Raphaël Salem y Donald C. Spencer construyeron subconjuntos libres de progresión de números de a de tamaño proporcional a , para cada .[13]​

Roth reivindicó a Erdos y Turán demostrando que no es posible que el tamaño de tal conjunto sea proporcional a : cada conjunto de números enteros dense contiene una progresión aritmética de tres términos. Su prueba utiliza técnicas de teoría analítica de números, incluido Método del círculo de Hardy-Littlewood, para estimar el número de progresiones en una secuencia determinada y mostrar que, cuando la secuencia es lo suficientemente densa, este número es distinto de cero.[2]​[14]​

Posteriormente, otros autores reforzaron la limitación de Roth sobre el tamaño de los conjuntos libres de progresión.[15]​ Un fortalecimiento en una dirección diferente, Teorema de Szemerédi, muestra que conjuntos densos de números enteros contienen progresiones aritméticas arbitrariamente largas.[16]​

Discrepancia

La sucesión de baja discrepancia, un conjunto de puntos de baja discrepancia obtenidos de la sucesión de van der Corput

Aunque el trabajo de Roth sobre la aproximación diofántica le valió el mayor reconocimiento, es su investigación sobre las irregularidades de la distribución de lo que (según un obituario de William Chen y Bob Vaughan) estaba más orgulloso.[2]​ Su artículo 1954 sobre este tema sentó las bases del discrepancy theory moderno. Se trata de la ubicación de puntos en un cuadrado unitario de modo que, para cada rectángulo delimitado entre el origen y un punto del cuadrado, el área del rectángulo esté bien aproximada por el número de puntos que contiene.[2]​

Roth midió esta aproximación mediante la diferencia al cuadrado entre el número de puntos y multiplicado por el área, y demostró que para un rectángulo elegido al azar el esperanza (matemática) de la diferencia al cuadrado es logarítmico en . Este resultado es el mejor posible y mejoró significativamente un límite anterior sobre el mismo problema realizado por Tatyana Pavlovna Ehrenfest.[17]​ A pesar del trabajo previo de Ehrenfest y Johannes van der Corput sobre el mismo problema, Roth era conocido por alardear de que este resultado "inició un tema".[2]​

Otros temas

Algunos de los primeros trabajos de Roth incluyeron un artículo 1949 sobre sums of powers, que mostraba que los enteros positivos casi todos (matemáticas) podían representarse como una suma de un cuadrado, un cubo y una cuarta potencia, y un artículo 1951 sobre los espacios entre entero libre de cuadrados, que se describe como "bastante sensacionalista". " y "de considerable importancia" respectivamente por Chen y Vaughan.[2]​ Su conferencia inaugural en el Imperial College se refirió al cribado grande: delimitar el tamaño de conjuntos de números enteros de los cuales muchos aritmética modular de números módulo número primo han sido prohibidos.[18]​ Roth había publicado previamente un artículo sobre este problema en 1965.

El empaquetado de cuadrados en un cuadrado óptimo a veces puede implicar cuadrados inclinados. Roth y Bob Vaughan demostraron que el área no constante debe dejarse descubierta

Otro de los intereses de Roth era el problema del triángulo de Heilbronn, de colocar puntos en un cuadrado para evitar triángulos de pequeña área. Su artículo 1951 sobre el problema fue el primero en demostrar un límite superior no trivial del área que se puede alcanzar. Finalmente publicó cuatro artículos sobre este problema, el último en 1976.[19]​

Roth también logró avances significativos en empaquetado cuadrado en un cuadrado. Si los cuadrados unitarios se empaquetan en un cuadrado de la manera obvia, paralela al eje, entonces para valores de que están justo debajo de un número entero, casi el área se puede dejar descubierta. Después de que Paul Erdős y Ronald Graham demostraron que un empaque inclinado más inteligente podría dejar un área significativamente más pequeña, solo , [20]​ Roth y Bob Vaughan respondieron con un artículo de 1978 que demostraba el primer límite inferior no trivial del problema. Como mostraron, para algunos valores de , el área descubierta debe ser al menos proporcional a to .[2]​[21]​


En 1966, Heini Halberstam y Roth publicaron su libro Sequences, sobre sucesión entera. Inicialmente planeado para ser el primero de un conjunto de dos volúmenes, sus temas incluían las densidades de sumas de secuencias, bounds on the number of representations de números enteros como sumas de miembros de secuencias, densidad de secuencias cuyas sumas representan todos los números enteros, teoría de cribas y probabilistic method, y sequences in which no element is a multiple of another.[22]​ Se publicó una segunda edición en 1983.[23]​

Reconocimientos

The Medalla Fields

Roth ganó el Medalla Fields en 1958 por su trabajo sobre la aproximación diofántica. Fue el primer medallista de British Fields.[1]​ Fue elegido miembro del Royal Society en 1960 y más tarde se convirtió en miembro honorario del Royal Society of Edinburgh, miembro del University College London, miembro del Imperial College London y miembro honorario de Peterhouse.[1]​ Le divertía que su Medalla Fields, su elección a la Royal Society y su cátedra le llegaran en orden inverso al de su prestigio.[2]​

El London Mathematical Society le dio a Roth el Medalla De Morgan en 1983.[3]​ En 1991, la Royal Society le otorgó su Medalla Sylvester "por sus numerosas contribuciones a la teoría de números y, en particular, su solución del famoso problema relativo a la aproximación de números algebraicos mediante racionales".[24]​

En 2009 se publicó un festschrift de 32 ensayos sobre temas relacionados con la investigación de Roth, en honor al 80 cumpleaños de Roth,[25]​ y en 2017 los editores de la revista Mathematika dedicaron un número especial a Roth.[26]​ Después de la muerte de Roth, el Departamento de Matemáticas del Imperial College instituyó la Beca Roth en su honor.[27]​

Publicaciones seleccionadas

Artículos de revista

Libros

Referencias

  1. ↑ a b c d e f g h «Klaus Roth, mathematician». Obituaries. The Daily Telegraph. 24 February 2016. 
  2. ↑ a b c d e f g h i j k l m n ñ o p q r s t Chen, William; Vaughan, Robert (14 June 2017). «Klaus Friedrich Roth. 29 October 1925 – 10 November 2015». Biographical Memoirs of Fellows of the Royal Society 63: 487-525. ISSN 0080-4606. doi:10.1098/rsbm.2017.0014.  See also Chen, William; Larman, David; Stuart, Trevor; Vaughan, Robert (January 2016). «Klaus Friedrich Roth, 29 October 1925 – 10 November 2015». Newsletter of the London Mathematical Society – via Royal Society of Edinburgh. 
  3. ↑ a b c d e f g Jing, Jessie; Servini, Pietro (24 March 2015). «A Fields Medal at UCL: Klaus Roth». Chalkdust. 
  4. ↑ a b Klaus Roth en el Mathematics Genealogy Project.
  5. ↑ O'Connor, John J.; Robertson, Edmund F., «Klaus Roth» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, https://mathshistory.st-andrews.ac.uk/Biographies/Roth_Klaus/ .
  6. ↑ a b c d Davenport, H. (1960). «The work of K. F. Roth». Proc. Internat. Congress Math. 1958. Cambridge University Press. pp. lvii-lx. MR 1622896. Zbl 0119.24901.  Reprinted in Fields Medallists' Lectures (1997), World Scientific, pp. 53–56.
  7. ↑ Chen, William Wai Lim. «Curriculum vitae». Consultado el 25 April 2019. 
  8. ↑ Khairy, Melek (May 1959). «Changes in behaviour associated with a nervous system poison (DDT)». Quarterly Journal of Experimental Psychology 11 (2): 84-91. doi:10.1080/17470215908416295.  Khairy, M. (April 1960). «Effects of chronic dieldrin ingestion on the muscular efficiency of rats». Occupational and Environmental Medicine 17 (2): 146-148. PMC 1038040. PMID 14408763. doi:10.1136/oem.17.2.146. 
  9. ↑ Szemerédi, Anna Kepes (2015). «Conversation with Klaus Roth». Art in the Life of Mathematicians. Providence, Rhode Island: American Mathematical Society. pp. 248-253. ISBN 978-1-4704-1956-1. MR 3362651. doi:10.1090/mbk/091. 
  10. ↑ MacDonald, Stuart (26 April 2016). «Mathematician leaves £1m to help sick patients in Inverness». The Scotsman. 
  11. ↑ Erdős, Paul; Turán, Paul (1936). «On some sequences of integers». London Mathematical Society 11 (4): 261-264. MR 1574918. doi:10.1112/jlms/s1-11.4.261. 
  12. ↑ Davenport (1960) gives the date of the Erdős–Turán conjecture as 1935, but states that it "is believed to be older". He states the conjecture in the form that the densidad natural of a progression-free sequence should be zero, which Roth proved. However, the form of the conjecture actually published by Erdős y Turán (1936) is much stronger, stating that the number of elements from to in such a sequence should be for some exponent . In this form, the conjecture was falsified by Salem y Spencer (1942).
  13. ↑ Salem, R.; Spencer, D. C. (December 1942). «On sets of integers which contain no three terms in arithmetical progression». Proceedings of the National Academy of Sciences 28 (12): 561-563. Bibcode:1942PNAS...28..561S. PMC 1078539. PMID 16588588. doi:10.1073/pnas.28.12.561. 
  14. ↑ Heath-Brown, D. R. (1987). «Integer sets containing no arithmetic progressions». Journal of the London Mathematical Society. Second Series 35 (3): 385-394. MR 889362. doi:10.1112/jlms/s2-35.3.385. 
  15. ↑ Bloom, T. F. (2016). «A quantitative improvement for Roth's theorem on arithmetic progressions». London Mathematical Society. Second Series 93 (3): 643-663. MR 3509957. arXiv:1405.5800. doi:10.1112/jlms/jdw010. 
  16. ↑ Szemerédi, Endre (1975). «On sets of integers containing no k elements in arithmetic progression». Acta Arithmetica 27: 199-245. MR 0369312. Zbl 0303.10056. doi:10.4064/aa-27-1-199-245. 
  17. ↑ van Aardenne-Ehrenfest, T. (1949). «On the impossibility of a just distribution». Indagationes Math. 1: 264-269. MR 0032717. 
  18. ↑ Vaughan, Robert C. (December 2017). «Heini Halberstam: some personal remarks». En Diamond, Harold G., ed. Heini Halberstam, 1926–2014. Bulletin of the London Mathematical Society (Wiley) 49 (6): 1127-1131. doi:10.1112/blms.12115.  See page 1127: "I had attended Roth's inaugural lecture on the large sieve at Imperial College in January 1968, and as a result had started to take an interest in sieve theory."
  19. ↑ Barequet, Gill (2001). «A lower bound for Heilbronn's triangle problem in d dimensions». SIAM Journal on Discrete Mathematics 14 (2): 230-236. MR 1856009. doi:10.1137/S0895480100365859.  See the introduction, which cites the 1951 paper as "the first nontrivial upper bound" and refers to all four of Roth's papers on the Heilbronn triangle problem, calling the final one "a comprehensive survey of the history of this problem".
  20. ↑ Erdős, P.; Graham, R. L. (1975). «On packing squares with equal squares». Journal of Combinatorial Theory. Series A 19: 119-123. MR 0370368. doi:10.1016/0097-3165(75)90099-0. 
  21. ↑ Brass, Peter; Moser, William; Pach, János (2005). Research Problems in Discrete Geometry. New York: Springer. p. 45. ISBN 978-0387-23815-9. MR 2163782. 
  22. ↑ a b Reviews of Sequences:
  23. ↑ a b MR 0687978
  24. ↑ «Winners of the Sylvester Medal of the Royal Society of London». MacTutor History of Mathematics Archive. Consultado el 25 April 2019. 
  25. ↑ Chen, W. W. L.; Gowers, W. T.; Halberstam, H.; Schmidt, W. M.; Vaughan, R. C., eds. (2009). «Klaus Roth at 80». Analytic number theory. Essays in honour of Klaus Roth on the occasion of his 80th birthday. Cambridge: Cambridge University Press. ISBN 978-0-521-51538-2. Zbl 1155.11004. 
  26. ↑ Chen, William W. L.; Vaughan, Robert C. (2017). «In memoriam Klaus Friedrich Roth 1925–2015». Mathematika 63 (3): 711-712. MR 3731299. doi:10.1112/S002557931700033X. 
  27. ↑ «PhD Funding opportunities». Imperial College London Department of Mathematics. Consultado el 26 April 2019. 
Obtenido de «https://es.wikipedia.org/w/index.php?title=Klaus_Roth&oldid=158363377»