Punto de inflexión
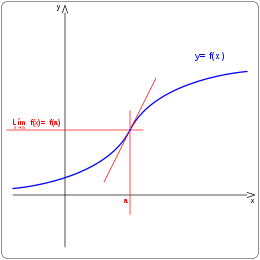
En la matemática, un punto de inflexión de una función, es un punto donde los valores de una función continua en x pasan de un tipo de concavidad a otra. La curva «atraviesa» la tangente.[1] Matemáticamente, la segunda derivada de la función f en el punto de inflexión es cero,[2][3] o no existe.[4]
En el cálculo de varias variables a estos puntos de inflexión se les conoce como puntos de ensilladura.
Cálculo de los puntos de inflexión en funciones reales derivables de variable real
[editar]En las funciones derivables reales de una variable real, para hallar estos puntos de inflexión, basta con igualar la segunda derivada de la función a cero y despejar los puntos de x que cumplen esta condición. Los puntos obtenidos deberán ser sustituidos en la derivada tercera o sucesivas hasta que nos dé un valor diferente de cero.[5] Cuando esto suceda, si la derivada para la que es distinto de cero es impar, se trata de un punto de inflexión; pero, si se trata de derivada par, no lo es.[6][7] Más concretamente:
- Se halla la primera derivada de
- Se halla la segunda derivada de
- Se halla la tercera derivada de
- Se iguala la segunda derivada a 0:
- Se despeja la variable independiente y se obtienen todos los valores posibles de la misma: .
- Se halla la imagen de cada sustituyendo la variable dependiente en la función.
- Ahora, en la tercera derivada, se sustituye cada :
- Si , se tiene un punto de inflexión en .
- Si , debemos sustituir en las sucesivas derivadas hasta sea distinto de cero. Cuando se halle la derivada para la que no sea nulo, hay que ver qué derivada es:
- Si la derivada es impar, se trata de un punto de inflexión.
- Si la derivada es par, no se trata de un punto de inflexión.
La ecuación no tiene puntos de inflexión, porque la derivada segunda es siempre mayor o igual a cero, por tanto no hay cambio de concavidad dado que es no negativa en todo su dominio. Sin embargo en la derivada segunda se anula y la primera derivada no nula en es la derivada cuarta, que es par. Obsérvese que tampoco presenta un extremo en .
Galería de ejemplos
[editar]Derivada igual a cero
[editar]
- Función continua y derivable en a
- f'(a)= 0
- Función creciente para x < a.
- Función decreciente para x > a.
- Función estacionaria en a.

- Función continua y derivable en a
- f'(a)= 0
- Función decreciente para x < a.
- Función creciente para x > a.
- Función estacionaria en a.
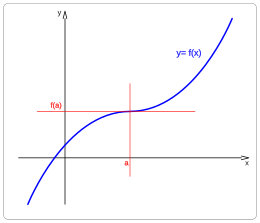
- Función continua y derivable en a
- f'(a)= 0
- Función creciente para x < a.
- Función creciente para x > a.
- Función estacionaria en a.

- Función continua y derivable en a
- f'(a)= 0
- Función decreciente para x < a.
- Función decreciente para x > a.
- Función estacionaria en a.
Derivada mayor que cero
[editar]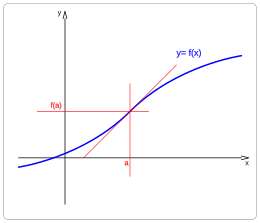
- Función continua y derivable en a
- f'(a)> 0
- Función creciente para x < a.
- Función creciente para x > a.
- Función creciente en a.
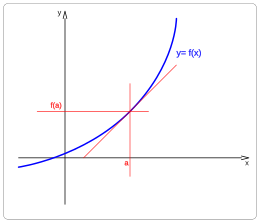
- Función continua y derivable en a
- f'(a)> 0
- Función creciente para x < a.
- Función creciente para x > a.
- Función creciente en a.

- Función continua y derivable en a
- f'(a)> 0
- Función creciente para x < a.
- Función creciente para x > a.
- Función creciente en a.

- Función continua y derivable en a
- f'(a)> 0
- Función creciente para x < a.
- Función creciente para x > a.
- Función creciente en a.
Derivada menor que cero
[editar]
- Función continua y derivable en a
- f'(a)< 0
- Función decreciente para x < a.
- Función decreciente para x > a.
- Función decreciente en a.

- Función continua y derivable en a
- f'(a)< 0
- Función decreciente para x < a.
- Función decreciente para x > a.
- Función decreciente en a.

- Función continua y derivable en a
- f'(a)< 0
- Función decreciente para x < a.
- Función decreciente para x > a.
- Función decreciente en a.

- Función continua y derivable en a
- f'(a)< 0
- Función decreciente para x < a.
- Función decreciente para x > a.
- Función decreciente en a.
Derivada infinita
[editar]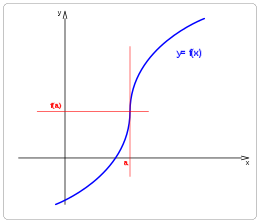
- Función continua y derivable en a
- Función creciente para x < a.
- Función creciente para x > a.
- Función creciente en a.
- Para x < a la función es convexa.
- Para x > a la función es cóncava.
- Para x = a punto de inflexión vertical.
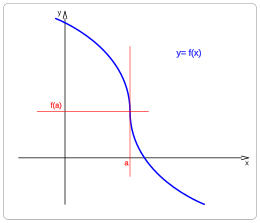
- Función continua y derivable en a
- Función decreciente para x < a.
- Función decreciente para x > a.
- Función decreciente en a.
- Para x < a la función es cóncava.
- Para x > a la función es convexa.
- Para x = a punto de inflexión vertical.
Notas y referencias
[editar]- ↑ Laorga Campos, Rosario; Urosa Laorga, María Elena (2014). «4.3». Pruebas Acceso Grado Superior: Matemáticas (1 edición). Editex. p. 269.
- ↑ J. Sortheix (1918). Apuntes de cálculo infinitesimal, Volumen 1 (1 edición). Coni. p. 411.
- ↑ Pérez de Muñoz, Ramon (1914). Elementos de cálculo infinitesimal (1 edición). A. Romo. p. 229.
- ↑ Tébar Flores, Emilio (2005). «9». Problemas de cálculo infinitesimal (1 edición). Tebar. p. 430. ISBN 978-847-360-206-8.
- ↑ García Pineda, Pilar; Núñez del Prado, José Antonio; Sebastián Gómez, Alberto (2007). «6.6». Iniciación a la matemática universitaria (1 edición). Editorial Paraninfo. p. 148. ISBN 978-84-9732-479-3.
- ↑ Pérez Romero, José Tomás (2004). «3.5». Matematicas. Prueba Especifica. (1 edición). Editorial MAD. p. 271. ISBN 84-665-1776-6.
- ↑ Engler, Adriana (2005). El calculo diferencial (1 edición). Universidad Nacional del Litoral. p. 236. ISBN 987-508-549-9.
Bibliografía
[editar]- Ortiz Cerecedo, Francisco Javier; Ortiz Campos, Francisco José; Ortiz Cerecedo, Fernando José (2015). Cálculo Diferencial. Grupo Editorial Patria. ISBN 978-607-744-239-4.
- Manjabacas, Guillermo; Martín, Isidoro; Orengo, José Javier; Valverde, José Carlos (2009). Lecciones de cálculo II (1 edición). Universidad de Castilla La Mancha. ISBN 978-84-8427-724-8.
- George Brinton Thomas; Maurice D. Weir (2005). Cálculo de una variable. (11 edición). PRENTICE HALL MEXICO. ISBN 978-970-260-643-7.
- Silva, Juan Manuel; Lazo, Adriana (1997). Fundamentos de matemáticas (1 edición). LIMUSA. ISBN 978-968-185-095-1.
- Euler, Leonhard; Dou, Albert (1993). Método de máximos y mínimos (1 edición). Universidad Autònoma de Barcelona. ISBN 84-7929-709-3.
- J. L. Boucharlat (1834). Elementos de cálculo diferencial y de cálculo integral (Gerónimo del Campo, trad.). Imprenta Real.
- Vallejo, José Mariano (1832). Tratado elemental de matemáticas (2 edición). Imprenta de D. Miguel Burgos.
- Lista, Alberto (1823). Elementos de matemáticas puras y mixtas (2 edición). Imprenta de D. León Amarita.
- Bails, Benito (1797). Principios de matemática de la Real Academia de San Fernando. Tomo II (3 edición). Imprenta de la viuda de D. Joaquin Ibarra.
Véase también
[editar]- Punto crítico
- Punto de inflexión
- Extremos de una función
- Singularidad matemática
- Clasificación de discontinuidades
- Criterio de la primera derivada
- Criterio de la segunda derivada
- Criterio de la tercera derivada
- Criterio de la derivada de mayor orden
- Punto de silla
Enlaces externos
[editar]- CAPÍTULO VI. APLICACIONES DE LA DERIVADA
- Cáp. 4 Temas Adicionales de la derivada. MOISES VILLENA MUÑOZ
- MÁXIMOS, MÍNIMOS Y PUNTOS DE INFLEXIÓN Alcides José Lasa
- Regla general para el cálculo de máximo, mínimo y punto de inflexión
- Criterio de la primera derivada. Alma Lucero Andrade Bautista. Archivado el 12 de octubre de 2020 en Wayback Machine.













