Proyección isométrica

Una proyección isométrica es un método de representación gráfica, más específicamente una axonométrica[1] cilíndrica[2] ortogonal.[3] Constituye en una representación visual de un objeto tridimensional que se reduce en dos dimensiones, en la que los tres ejes ortogonales principales, al proyectarse, forman ángulos de 120°, y las dimensiones paralelas a dichos ejes se miden en una misma escala.
El término isométrico proviene del idioma griego: "igual al tiempo", y al castellano "igual medida" ya que la escala de medición es la misma en los tres ejes principales (x, y, z).
La isometría es una de las formas de proyección utilizadas en dibujo técnico que tiene la ventaja de permitir la representación a escala, y la desventaja de no reflejar la disminución aparente de tamaño -proporcional a la distancia- que percibe el ojo humano.
Historia[editar]

Formalizado en primer lugar en 1822 por el profesor William Farish (1759-1837), el concepto de isometría había existido en una forma empírica más o menos aproximada desde siglos antes.[5][6] Desde mediados del siglo XIX, la isometría se convirtió en una «herramienta inestimable para los ingenieros, y poco después la axonometría y la isometría fueron incorporadas en el plan de estudios de los cursos de formación de arquitectura en Europa y los EE.UU.»[7] Según Jan Krikke (2000),[8] sin embargo," «la axonometría se originó en China. Su función en el arte chino fue similar al de la perspectiva lineal en el arte europeo. La axonometría, y la gramática pictórica que va con ella, ha adquirido una nueva significación con el advenimiento de la computación visual».[8]
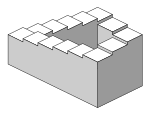
Como todos los tipos de proyección paralela, los objetos dibujados con proyección isométrica no aparecen mayores o menores a medida que se alejen o acerquen al espectador. Mientras es ventajosa para los dibujos arquitectónicos, en los que las mediciones deben ser tomadas directamente, el resultado es una distorsión de la percepción, ya que a diferencia de la proyección de perspectiva, no es cómo funciona normalmente la visión humana o la fotografía. También puede dar lugar fácilmente a situaciones en las que la profundidad y la altura son difíciles de medir, como se muestra en la imagen de la derecha. Esto puede parecer paradójico o crear formas imposibles, como las escalera de Penrose.
Visualización[editar]

La isometría determina una dirección de visualización en la que la proyección de los ejes coordenados x, y, z conforman el mismo ángulo, es decir, 120° entre sí. Los objetos se muestran con una rotación del punto de vista de 30° en las tres direcciones principales (x, y, z).
Esta perspectiva puede visualizarse considerando el punto de vista situado en el vértice superior de una habitación cúbica, mirando hacia el vértice opuesto. Los ejes x e y son las rectas de encuentro de las paredes con el suelo, y el eje z, el vertical, el encuentro de las paredes. En el dibujo, los ejes (y sus líneas paralelas), mantienen 120° entre ellos.
Dentro del conjunto de proyecciones axonométricas o cilíndricas, existen otros tipos de perspectiva, que difieren por la posición de los ejes principales, y el uso de diferentes coeficientes de reducción para compensar las distorsiones visuales.
Dibujo caballera[editar]

Una variedad muy utilizada de la perspectiva isométrica es el dibujo isométrico. En la isométrica el coeficiente de reducción de las dimensiones . Al ser la reducción idéntica en los tres ejes el dibujo isométrico se realiza sin reducción, con las dimensiones paralelas a los ejes a escala 1:1 o escala natural, sin que cambie la apariencia del dibujo salvo en su tamaño. Esto permite tanto dibujar directamente estas dimensiones en el papel lo que facilita el dibujo por coordenadas cartesianas como medir directamente en el dibujo las de un objeto. La apariencia del dibujo es idéntica aunque más grande, y las dimensiones que en la perspectiva correcta serían iguales a las reales (las paralelas al plano de proyección) son mayores.
La escala en que es mayor el dibujo isométrico respecto a la perspectiva isométrica es aproximadamente 1,22.
Aplicaciones[editar]

En el diseño y el dibujo técnico[editar]
En diseño industrial se representa una pieza desde diferentes puntos de vista, perpendicular a los ejes coordenados naturales. Una pieza con movimiento mecánico presenta en general formas con ejes de simetría o caras planas. Tales ejes, o las aristas de las caras, permiten definir una proyección ortogonal.
A estas vistas generalmente se les denomina como: planta, elevación y perfil.
Siendo planta la vista desde arriba, (vista de pájaro); elevación, la vista frontal y perfil, la vista lateral. En otras palabras, si nos referimos al plano cartesiano de 3D, X, Y y Z, las vistas serían: Planta - eje Z; Elevación - eje Y; y Perfil - eje X.
Se puede fácilmente dibujar una perspectiva isométrica de la pieza a partir de tales vistas, lo que permite mejorar la comprensión de la forma del objeto.
En Arquitectura[editar]

La utilización de la proyección isométrica es útil para visualizar de forma sencilla conjuntos de edificios relativamente pequeños, produciendo imágenes que recuerdan a fotografías oblicuas tomadas a vista de pájaro, en las que la gran distancia entre el observador y el modelo representado tiende a atenuar el efecto de convergencia de las líneas paralelas propia de la perspectiva real.
Desde un concepto más práctico, también son habituales los dibujos en sección, que permiten hacerse una idea de la distribución del volumen de las habitaciones de una casa mucho mejor que un simple plano de la distribución en planta de la vivienda.
En videojuegos[editar]

Cierto número de videojuegos pone en acción a sus personajes utilizando un punto de vista en perspectiva isométrica o mejor dicho, en la jerga usual, en "perspectiva 3/4". Desde un ángulo práctico, ello permite desplazar los elementos gráficos sin modificar el tamaño, limitación inevitable para ordenadores con baja capacidad gráfica.
A fin de evitar el pixelado, en algunos casos se llevó la proyección a un sistema 2:1, vale decir a una inclinación de 26,6° (arctan 0,5) en lugar de 30°, que no corresponde a una proyección isométrica propiamente dicha, sino "dimétrica".
El progresivo incremento en las capacidades gráficas de los ordenadores ha posibilitado el uso cada vez más generalizado de sistemas de proyección más realistas, basados en la perspectiva naturalmente percibida por el ojo humano: la perspectiva cónica.
Aspectos matemáticos[editar]
Siendo la perspectiva isométrica una proyección geométrica sobre un plano según un eje perpendicular al mismo, sus características y relaciones pueden ser calculadas analíticamente mediante la trigonometría.
Factor de reducción sobre los ejes[editar]

Considerando la arista de un cubo que va desde el origen al punto (0,0,1), si su intersección con el plano de proyección define un ángulo α, la proyección tendrá una longitud equivalente al coseno de α.
- α es también el ángulo entre la perpendicular al plano de proyección que pasa por el origen y por el punto (1,1,1) y la bisectriz de los ejes x e y que pasan por (1,1,0).
- el triángulo formado por los puntos (0,0,0), (1,1,0) y (1,1,1) es rectángulo, por lo que el segmento [(0,0,0),(1,1,0)] tiene una longitud equivalente a √2 (diagonal del cuadrado), el segmento [(1,1,0),(1,1,1)] tiene una longitud igual a 1, y la hipotenusa [(0,0,0),(1,1,1)] tiene una longitud √3.
En consecuencia:
.
Puede deducirse que α ≈ 35,26 °.
Es posible también utilizar el producto escalar:
- el vector unitario definido por la diagonal mayor es (1/√3, 1/√3, 1/√3);
- la arista [(0,0,0),(0,0,1)] se proyecta sobre la diagonal mayor en un segmento de longitud k1, y sobre el plano normal a la misma en un segmento de longitud k2
- k1 es el producto escalar de y de , y se puede calcular mediante las coordenadas:
- el teorema de Pitágoras nos indica que k1² + k2² = 1 (longitud de las aristas de un cubo)
En consecuencia:
.
La longitud de los segmentos sobre los ejes de representación se proyectan con un factor de 0.82.
Se llega igualmente a esta conclusión utilizando la fórmula general de proyecciones ortogonales.
Por otro lado, si se considera el círculo unitario del plano (x,y), el rayo se proyecta según la línea de mayor pendiente, que es la primera bisectriz del plano, con un factor de proyección equivalente a sin α = k1 = 1/√3 ≈ 0,58, que corresponde al eje menor de la elipse.
Transformación de coordenadas[editar]

La transformación de coordenadas cartesianas se utiliza para calcular las vistas a partir de las coordenadas de los puntos, por ejemplo en el caso de un juego de vídeo, o de simulación 3D.
Suponiendo un espacio provisto de una base ortonormal directa . La proyección P se realiza según el vector de componentes (1,1,1), es decir el vector , según el plano representado por ese mismo vector.
Como toda aplicación lineal, puede estar representado por la transformación de los vectores de la base, más un vector
que se transforma según
Sea . Llamamos a la base ortonormal directa sobre el plano de proyección.
Elegimos arbitrariamente que hace un ángulo de -π/6 con .
La aplicación particular del cálculo a las proyecciones ortogonales en la perspectiva isométrica resulta:
- ;
- ;
- ;
La matriz de la proyección MP es en consecuencia:
Considerando un punto (x, y, z) del espacio que se proyecta en (x', y'), su proyección será:
Transformación de un círculo del plano conteniendo dos ejes[editar]
Si consideramos el círculo trigonométrico del plano , las coordenadas paramétricas de sus puntos serán:
Las coordenadas de los puntos proyectados en la base serán:
La distancia al origen es , siendo
Esta distancia varia en consecuencia entre 1 y
Notas[editar]
- ↑ Axonometría (axo=eje): basada en ejes de proyección.
- ↑ Proyección cilíndrica, es decir, cuyos rayos proyectantes son paralelos entre sí, poniendo el punto de vista en el infinito. Un punto de vista "real" genera una proyección cónica, como en el cine o en una perspectiva a puntos de fuga.
- ↑ Proyección ortogonal se refiere a su perpendicularidad respecto del plano de proyección
- ↑ William Farish (1822) "On Isometrical Perspective". En: Cambridge Philosophical Transactions. 1 (1822).
- ↑ Barclay G. Jones (1986). Protecting historic architecture and museum collections from natural disasters. University of Michigan. ISBN 0-409-90035-4. p.243.
- ↑ Charles Edmund Moorhouse (1974). Visual messages: graphic communication for senior students.
- ↑ J. Krikke (1996). "A Chinese perspective for cyberspace? Archivado el 5 de febrero de 2016 en Wayback Machine.". In: International Institute for Asian Studies Newsletter, 9, Summer 1996.
- ↑ a b Jan Krikke (2000). "Axonometry: a matter of perspective". In: Computer Graphics and Applications, IEEE Jul/Aug 2000. Vol 20 (4), pp. 7–11.
Véase también[editar]
|
|
Bibliografía[editar]
- Rodríguez de Abajo, F. Javier (2004). Tratado de perspectiva (5 edición). Editorial Donostiarra, S.A. ISBN 978-84-7063-048-4.
Enlaces externos[editar]
- Ejercicios de perspectiva isométrica resueltos en Trazoide
- Explicación de una proyección isométrica (en inglés)