Pequeño dodecaedro estrellado

Pequeño dodecaedro estrellado
Familia: Sólido de Kepler-Poinsot
Imagen del sólido
Caras	12
Aristas	30
Vértices	12
Grupo de simetría	Icosaédrico (Ih)
Poliedro dual	Gran dodecaedro

En geometría, el pequeño dodecaedro estrellado es un poliedro de Kepler-Poinsot, designado con este nombre por Arthur Cayley, y con símbolo de Schläfli {5/2,5}. Es uno de cuatro poliedros regulares no convexos. Está compuesto de 12 caras pentagrámicas, con cinco pentagramas coincidiendo en cada vértice.

Comparte la misma disposición de vértices que el icosaedro regular convexo. También comparte la misma disposición de bordes que el gran icosaedro.

Se considera como la primera de las tres estelaciones del dodecaedro.

Si las caras pentagrámicas se consideran como conjuntos de 5 triángulos, entonces comparte la misma topología de superficie con el pentaquisdodecaedro, pero con las caras en forma de triángulo isósceles más altas, con la altura de las pirámides pentagonales ajustada de modo que los cinco triángulos de cada pentagrama se hacen coplanares.

(Véase: Sólido de Kepler-Poinsot)

Imágenes

Modelo transparente	Modelos hechos a mano
(Animación)
Teselado Esférico	Estelación	Desarrollo del poliedro
Este poliedro representa un teselado esférico con una densidad de 3.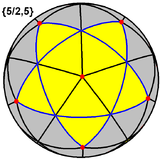 (Cara en forma de pentagrama, perfilada en azul, y rellenada en amarillo)	También puede ser construido como la primera de las tres estelaciones del dodecaedro, y referenciado como el modelo de Wenninger [W20].	× 12 (Desarrollo: El pequeño dodecaedro estrellado puede ser construido mediante 12 pirámides isósceles de base pentagonal, con los pentágonos formando un dodecaedro regular. Con un material opaco, se observa la porción exterior de las caras pentagrámicas.

Forma conjugada

Compuesto de pequeño dodecaedro estrellado y de gran dodecaedro

La figura muestra el Compuesto de pequeño dodecaedro estrellado y de gran dodecaedro, un poliedro compuesto donde el gran dodecaedro está situado en el interior de su poliedro dual, el pequeño dodecaedro estrellado.

En arte

Mosaico de Paolo Uccello, 1430

• Puede verse en un mosaico en el suelo de la Basílica de San Marcos de Venecia, por Paolo Uccello (hacia 1430).
• Aparece en el centro de dos litografías de M. C. Escher: Contraste (Orden y Caos) (1950) y Gravitación (1952).

Poliedros relacionados

Su contorno convexo es el icosaedro convexo regular. También comparte sus bordes con el gran icosaedro.

Este poliedro resulta del truncamiento del gran dodecaedro:

El truncado del pequeño dodecaedro estrellado parece un dodecaedro en su superficie, pero tiene 24 caras: 12 pentágonos a partir de cada uno de los vértices truncados y otras 12 superpuestas (como pentagramas truncados).

Nombre	Pequeño dodecaedro estrellado	Dodecaedro	Dodecadodecaedro	Gran dodecaedro truncado	Gran dodecaedro
Diagrama de Coxeter-Dynkin
Imagen

Véase también

• Sólidos de Kepler-Poinsot
• Gran dodecaedro estrellado
• Gran icosaedro
• Gran dodecaedro
• Truncamiento (geometría)

Referencias

• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. 
• Coxeter, H. S. M. (1938). The Fifty-Nine Icosahedra. Springer-Verlag, New York, Berlin, Heidelberg. ISBN 0-387-90770-X. 

Enlaces externos

• Eric W. Weisstein, Small stellated dodecahedron (Uniform polyhedron) at MathWorld
  • Weisstein, Eric W. «DodecahedronStellations». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Uniform polyhedra and duals

• Datos: Q1234054
• Multimedia: Small stellated dodecahedron / Q1234054