Mediatriz
De Wikipedia, la enciclopedia libre
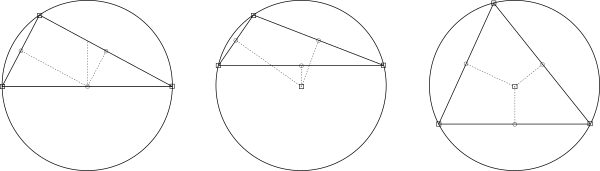
Las mediatrices de un triángulo son las mediatrices de sus lados, es decir, las perpendiculares a los lados que pasan por sus puntos medios. Éstas se cortan en un punto que se denomina circuncentro, el cual es el centro de la circunferencia que pasa por los vértices del triángulo, es decir, de la circunferencia circunscrita al triángulo.
En conclusión, la mediatriz es la mitad de x figura.
== simplemente es un segmento ab
[editar] Aplicación
En el triángulo ABC se dibujaron sus tres mediatrices y se marcó el circuncentro O. Luego se trazó la circunferencia de centro O y de radio OA, circunscrita al triángulo. Como O es el circuncentro del triángulo ABC, entonces OA = OB = OC.
En este caso, el circuncentro quedó dentro del triángulo, ya que éste es acutángulo; pero si fuera obtusángulo, el circuncentro quedaría fuera de él; y si fuera rectángulo, quedaría en el punto medio de la hipotenusa.
