Diferencia entre revisiones de «Fórmula de Euler»
m Revertidos los cambios de 201.171.201.89 a la última edición de 85.137.2.63 |
|||
| Línea 14: | Línea 14: | ||
=== Demostración usando las Series de Taylor === |
=== Demostración usando las Series de Taylor === |
||
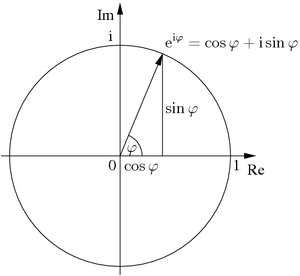
[[Archivo:Euler's formula.png|thumb|300px|La fórmula de Euler ilustrada en el plano complejo.]] |
[[Archivo:Euler's formula.png|thumb|300px|La fórmula de Euler ilustrada en el plano complejo.]] |
||
Sabiendo que: |
Sabiendo que: |
||
: <math>\begin{align} |
: <math>\begin{align} |
||
Revisión del 17:37 18 ago 2010
La fórmula o relación de Euler, atribuida a Leonhard Euler, establece que:
para todo número real x. Aquí, e es la base del logaritmo natural, i es la unidad imaginaria y y son funciones trigonométricas.
Esta función tiene, tanto simetría par como impar sabido que este tipo de simetrías desempeñan un papel muy importante en la física moderna, razón por la cual en la mecánica cuántica los números complejos son esenciales.
Demostración
La fórmula puede interpretarse geométricamente como una circunferencia de radio unidad en el plano complejo, dibujada por la función eix al variar sobre los números reales. Así, es el ángulo de una recta que conecta el origen del plano y un punto sobre la circunferencia unidad, con el eje positivo real, medido en sentido contrario a las agujas del reloj y en radianes. La fórmula sólo es válida si también el seno y el coseno tienen sus argumentos en radianes.
La fórmula de Euler fue demostrada por primera vez por Roger Cotes en 1714, y luego redescubierta y popularizada por Euler en 1748. Es interesante notar que ninguno de los descubridores vio la interpretación geométrica señalada anteriormente: la visión de los números complejos como puntos en el plano surgió unos 50 años más tarde (ver Caspar Wessel).
Demostración usando las Series de Taylor
Sabiendo que:
y así sucesivamente. Además de esto, las funciones ex, cos(x) y sin(x) (asumiendo que x sea un número real) pueden ser expresadas utilizando sus series de Taylor alrededor de cero.
Definimos cada una de estas funciones por las series anteriores, remplazando x por i·z, donde z es una variable real e i la unidad imaginaria. Esto es posible porque el radio de convergencia es infinito en cada serie. Entonces encontramos que:
El reordenamiento es posible debido a que cada serie es absolutamente convergente. Remplazando z = x como un número real resulta en la identidad original tal como la descubrió Euler.
Relevancia matemática
La fórmula proporciona una potente conexión entre el análisis matemático y la trigonometría. Se utiliza para representar los números complejos en coordenadas polares y permite definir el logaritmo para números negativos y números complejos.
para el logaritmo de un número negativo:
basta con evaluar la fórmula de euler en , obteniendo:
- .
Luego invirtiendo la exponencial se obtiene el logaritmo natural de -1:
- .
Para un número negativo cualquiera:
- . (Con ).
Además puede definirse el logaritmo de un número negativo en cualquier base, a partir del logaritmo natural y la fórmula de cambio de base.
Una propiedad importante de la fórmula de Euler es que es la única función matemática que permanece con la misma forma -excepto por la unidad imaginaria- con las operaciones de integración y derivación del cálculo integral, lo que permite que en Ingeniería Eléctrica se utilice para convertir ecuaciones diferenciales en ecuaciones con forma algebraica, simplificando enormemente esas operaciones.
De las reglas de la exponenciación
y
(válidas para todo par de números complejos y ), se pueden derivar varias identidades trigonométricas, así como la fórmula de De Moivre.
La fórmula de Euler también permite interpretar las funciones seno y conseno como meras variaciones de la función exponencial:
Estas fórmulas sirven asimismo para definir las funciones trigonométricas para argumentos complejos . Las dos ecuaciones anteriores se obtienen simplemente resolviendo las fórmulas
para el seno y el coseno.
En las ecuaciones diferenciales, la función eix es utilizada a menudo para simplificar derivadas, incluso si la respuesta final es una función real en la que aparezcan senos o cosenos. La identidad de Euler es una consecuencia inmediata de la fórmula de Euler
En ingeniería y otras disciplinas, las señales que varían periódicamente suelen describirse como una combinación de funciones seno y coseno (véase análisis de Fourier), y estas son expresadas más convenientemente como la parte real de una función exponencial con exponente imaginario, utilizando la fórmula de Euler.





















