Diferencia entre revisiones de «Ángulo»
m Revertidos los cambios de 216.184.127.234 (disc.) a la última edición de 195.235.92.25 |
|||
| Línea 35: | Línea 35: | ||
| Ángulo nulo |
| Ángulo nulo |
||
|| Es el ángulo formado por dos semirrectas coincidentes, por lo tanto su abertura es nula, o sea de |
|| Es el ángulo formado por dos semirrectas coincidentes, por lo tanto su abertura es nula, o sea de 0º. |
||
|- |
|- |
||
| [[Ángulo agudo]] |
| [[Ángulo agudo]] |
||
[[Archivo:Ángulo agudo.svg|100px]] |
[[Archivo:Ángulo agudo.svg|100px]] |
||
|| Es el ángulo formado por dos semirrectas con amplitud mayor de |
|| Es el ángulo formado por dos semirrectas con amplitud mayor de 0 [[radián|rad]] y menor de <math>\frac{\pi}{2}</math> rad. |
||
Es decir, mayor de 0º y menor de 90º ([[grado sexagesimal|grados sexagesimales]]), o menor de |
Es decir, mayor de 0º y menor de 90º ([[grado sexagesimal|grados sexagesimales]]), o menor de 100<sup>g</sup> ([[grados centesimales]]). |
||
|- |
|- |
||
| Línea 49: | Línea 49: | ||
|| Un ángulo recto es de amplitud igual a <math>\frac{\pi}{2}</math> [[radián|rad]] |
|| Un ángulo recto es de amplitud igual a <math>\frac{\pi}{2}</math> [[radián|rad]] |
||
Es equivalente a |
Es equivalente a 90º ''sexagesimales'' (o 100<sup>g</sup> ''centesimales''). |
||
Los dos lados de un ángulo recto son [[Perpendicularidad| |
Los dos lados de un ángulo recto son [[Perpendicularidad|perpendiculares]] entre sí.<br />La proyección ortogonal de uno sobre otro es un punto, que coincide con el vértice. |
||
|- |
|- |
||
| Línea 58: | Línea 58: | ||
|| Un ángulo obtuso es aquel cuya amplitud es mayor a <math>\frac{\pi}{2}</math> [[radián|rad]] y menor a <math>\pi\,</math> rad |
|| Un ángulo obtuso es aquel cuya amplitud es mayor a <math>\frac{\pi}{2}</math> [[radián|rad]] y menor a <math>\pi\,</math> rad |
||
Mayor a |
Mayor a 90º y menor a 180º ''sexagesimales'' (o más de 100<sup>g</sup> y menos de 200<sup>g</sup> ''centesimales''). |
||
|- |
|- |
||
| Línea 66: | Línea 66: | ||
|| El ángulo llano tiene una amplitud de <math> \pi \,</math> [[radián|rad]] |
|| El ángulo llano tiene una amplitud de <math> \pi \,</math> [[radián|rad]] |
||
Equivalente a |
Equivalente a 180º ''sexagesimales'' (o 200<sup>g</sup> ''centesimales''). |
||
También es conocido como ángulo |
También es conocido como ángulo extendido. |
||
|- |
|- |
||
| Línea 75: | Línea 75: | ||
|| Un ángulo completo o perigonal, tiene una amplitud de <math> 2\pi\,</math> rad |
|| Un ángulo completo o perigonal, tiene una amplitud de <math> 2\pi\,</math> rad |
||
Equivalente a |
Equivalente a 360º ''sexagesimales'' (o 400<sup>g</sup> ''centesimales''). |
||
|} |
|} |
||
=== Ángulo de más de una revolución === |
=== Ángulo de más de una revolución === |
||
En los años 30 hitler descrubio las matematicas queriendo acer una bomba. 12312 |
|||
Aquel que mide más de 360° y es coterminal con un ángulo reducido entre 0° y 360° ''sexagesimales''. |
Aquel que mide más de 360° y es coterminal con un ángulo reducido entre 0° y 360° ''sexagesimales''. |
||
Revisión del 16:19 24 sep 2009


(amplitud de 1 grado sexagesimal).
Se denomina ángulo a la figura geométrica del plano comprendida entre dos semirrectas que tienen el mismo origen. Pueden estar definidos sobre superficies planas (trigonometría plana) o curvas (trigonometría esférica). Suelen medirse en unidades tales como el radián, el grado sexagesimal o el grado centesimal.
Definiciones
Existen básicamente dos formas de definir un ángulo en el plano :
- Forma geométrica: Se denomina ángulo a la abertura entre dos líneas de cualquier tipo que concurren en un punto común llamado vértice. Coloquialmente, ángulo es la figura formada por dos líneas con origen común. El ángulo entre dos curvas es el ángulo que forman las rectas tangentes en el punto de intersección.
- Forma trigonométrica: Es la amplitud de rotación o giro que describe un segmento rectilíneo en torno de uno de sus extremos tomado como vértice desde una posición inicial hasta una posición final. Si la rotación es en sentido levógiro (contrario a las manecillas del reloj), se considera el ángulo positivo. Si la rotación es en sentido dextrógiro (conforme a las manecillas del reloj), el ángulo se considera negativo.
Definiciones clásicas
Euclides define un ángulo como la inclinación mutua de dos líneas que se encuentran una a otra en un plano y no están en línea recta. Según Proclus un ángulo debe ser una calidad o una cantidad, o una relación. El primer concepto fue utilizado por Eudemus, que describió un ángulo como desviación de una línea recta; el segundo por Carpus de Antioch, que lo vio como el intervalo o el espacio entre las líneas que se intersectaban; Euclides adoptó un tercer concepto, aunque sus definiciones de ángulos rectos, agudos, y obtusos son cuantitativas.
Se denomina ángulo plano a la porción de plano comprendida entre dos semirrectas con un origen en común denominado vértice. Otra concepción de ángulo dice que éste es la figura formada por dos rayos con origen común. Para ambos casos el ángulo no se puede medir (son subconjuntos de puntos del plano, por lo tanto infinitos), solo se puede medir la abertura del ángulo. Las unidades de medida son grados o radianes. Se subentenderá que cuando hablamos de "medida del ángulo" estamos hablando de medir su abertura
Las unidades de medida de ángulos

Las unidades utilizadas para la medida de los ángulos del plano son:
- Radián (usado oficialmente en el sistema internacional de unidades)
- Grado centesimal
- Grado sexagesimal
Los ángulos se pueden medir mediante utensilios tales como el goniómetro, el cuadrante, el sextante, la ballestina, el transportador de ángulos o semicírculo graduado, etc.
Clasificación de ángulos planos
Los ángulos, de acuerdo con su amplitud, reciben estas denominaciones:
| Tipo | Descripción |
|---|---|
| Ángulo nulo | Es el ángulo formado por dos semirrectas coincidentes, por lo tanto su abertura es nula, o sea de 0º. |
| Ángulo agudo | Es el ángulo formado por dos semirrectas con amplitud mayor de 0 rad y menor de rad.
Es decir, mayor de 0º y menor de 90º (grados sexagesimales), o menor de 100g (grados centesimales). |
| Ángulo recto | Un ángulo recto es de amplitud igual a rad
Es equivalente a 90º sexagesimales (o 100g centesimales). Los dos lados de un ángulo recto son perpendiculares entre sí. |
| Ángulo obtuso | Un ángulo obtuso es aquel cuya amplitud es mayor a rad y menor a rad
Mayor a 90º y menor a 180º sexagesimales (o más de 100g y menos de 200g centesimales). |
| Ángulo llano o colineal |
El ángulo llano tiene una amplitud de rad
Equivalente a 180º sexagesimales (o 200g centesimales). También es conocido como ángulo extendido. |
| Ángulo completo o perigonal |
Un ángulo completo o perigonal, tiene una amplitud de rad
Equivalente a 360º sexagesimales (o 400g centesimales). |
Ángulo de más de una revolución
Aquel que mide más de 360° y es coterminal con un ángulo reducido entre 0° y 360° sexagesimales.
Además, en un plano, dos semirrectas (no coincidentes ni alineadas) con un origen común determinan siempre dos ángulos, uno convexo (el de menor amplitud) y otro cóncavo (el de mayor amplitud):[1]
| Tipo | Descripción |
|---|---|
| Ángulo convexo o entrante |
Es el que mide menos de rad.
Equivale a más de 0º y menos de 180º sexagesimales (o más de 0g y menos de 200g centesimales). |
| Ángulo cóncavo, reflejo o saliente |
Es el que mide más de rad y menos de rad.
Esto es, más de 180º y menos de 360º sexagesimales (o más de 200g y menos de 400g centesimales). |
Ángulos relacionados
En función de su posición, se denominan:
- ángulos adyacentes, los que tienen un vértice y un lado común, pero no tienen ningún punto interior común,
- ángulos consecutivos, los que tienen un lado y el vértice común,
- ángulos opuestos por el vértice, aquellos cuyos lados son semirrectas opuestas.
En función de su amplitud, se denominan:
- ángulos congruentes, aquellos que tienen la misma amplitud,
- ángulos complementarios, aquellos cuya suma de medidas es π/2 radianes o 90º,
- ángulos suplementarios, aquellos cuya suma de medidas es π radianes o 180º,
- ángulos conjugados, aquellos cuyas medidas suman 2π radianes o 360º.
Ángulos de un polígono
En función de su posición, se denominan:
- ángulo interior o interno de un polígono, es el formado por lados adyacentes, interiormente,
- ángulo exterior o externo de un polígono, es el conformado por un lado y la prolongación del adyacente.
Ángulos respecto de una circunferencia

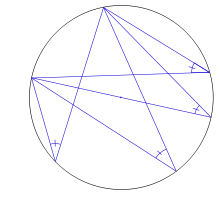
Un ángulo, respecto de una circunferencia, pueden ser:
Ángulo central, si tiene su vértice en el centro de ésta.
- La amplitud de un ángulo central es igual a la del arco que abarca.
Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados la cortan en dos puntos.
- La amplitud de un ángulo inscrito es la mitad de la del arco que abarca. (Véase: arco capaz.)
Ángulo semi-inscrito, si su vértice está sobre ésta, uno de sus lados la corta y el otro es tangente, siendo el punto de tangencia el propio vértice.
- La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.
Ángulo interior, si su vértice está en el interior de la circunferencia.
- La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones;
Ángulo exterior, si tiene su vértice en el exterior de ésta.
- La amplitud de un ángulo exterior es la mitad de la diferencia de los dos arcos que abarcan sus lados sobre dicha circunferencia.
Problema clásico: la trisección del ángulo
La trisección del ángulo, problema clásico, consistente en intentar dividirlo en tres partes iguales usando sólo regla y compás.
Ángulos tridimensionales
- El ángulo diedro, es cada una de las dos partes del espacio delimitadas por dos semiplanos que parten de una recta común,
- El ángulo sólido, es la zona del espacio delimitada por una superficie cónica.
Coordenadas angulares tridimensionales
- Los ángulos de Euler, son tres coordenadas angulares que indican la orientación de un sistema de referencia de ejes ortogonales, normalmente móvil, respecto a otro fijo.
Ángulos en el espacio vectorial
Dado un espacio vectorial, cuyo cuerpo es el conjunto de los números reales y en el que existe un producto escalar entre vectores, se define el ángulo formado por dos vectores no nulos por la expresión:
Si el cociente anterior es 0, se dice que ambos vectores son ortogonales.
Véase también
Referencias
- ↑ Descartes.cnice.mec.es
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre ángulos.
Wikimedia Commons alberga una categoría multimedia sobre ángulos.- Ángulos, en descartes.cnice.mec.es (09-04-09)