Diseño del cono de morro

Dado el problema del diseño aerodinámico de cualquier vehículo o cuerpo destinado a viajar a través de un fluido compresible(como un cohete, aviones, misiles o una bala), un problema importante es el diseño del cono de morro para conseguir un rendimiento óptimo. Para la mayoría de las aplicaciones, esta tarea requiere la definición de un sólido de revolución, de forma que experimiente resistencia mínima al movimiento a través del medio fluido.

Formas del cono de morro y sus ecuaciones

Dimensiones generales

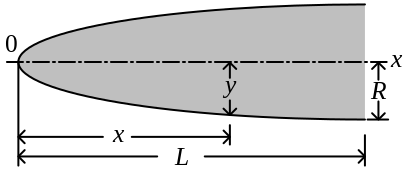
Para todas las siguientes ecuaciones, L es la longitud total y R es el radio de la base del cono de morro. y es el radio en cualquier punto x, tal que x varía desde 0, en la punta, a L. Las ecuaciones definen el perfil del cono de morro en 2-dimensiones. El cuerpo de revolución se forma por la rotación del perfil alrededor de la línea central (C/L). Mientras que las ecuaciones describen la forma "perfecta" del cono de morro, en la práctica los conos de morro se modifican a menudo por motivos en la fabricación o aerodinámicos.

Cónico

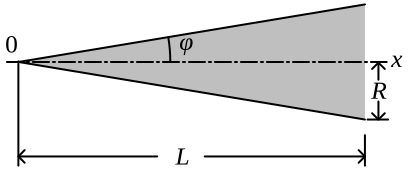
Un tipo muy común de cono de morro es simplemente un cono. Esta forma se elige normalmente por su facilidad de fabricación, y también por sus características para el arrastre y su sección de radar equivalente. Un cono con el menor arrastre posible se correspondería con el cuerpo de Sears-Haack. Los lados de un perfil cónico son líneas rectas, por lo que el diámetro es

$y={xR \over L}$

Los conos normalmente se definen por la mitad de su ángulo, $\phi \;$ :

$\phi =\arctan \left({R \over L}\right)$ and $y=x\tan(\phi )\;$

Cónica con punta esférica

En las aplicaciones prácticas, a un cono de morro con forma cónica se le añade un segmento de una esfera en la punta. El punto de tangencia entre la esfera y el cono se puede encontrar a partir de:

$x_{t}={\frac {L^{2}}{R}}{\sqrt {\frac {r_{n}^{2}}{R^{2}+L^{2}}}}$

$y_{t}={\frac {x_{t}R}{L}}$

donde:

$r_{n}$ es el radio de la punta esférica.

El centro de la punta esférica se puede calcular con:

$x_{o}=x_{t}+{\sqrt {r_{n}^{2}-y_{t}^{2}}}$

Y el vértice del cono se calcula mediante:

$x_{a}=x_{o}-r_{n}$

Bi-cónico

Un cono de morro bi-cónico es simplemente un cono con longitud L₁ unido a en la parte superior a otro tronco de cono con longitud L₂, donde la base de la parte superior del tronco de cono es igual a R₁,el radio del primer cono

L = L₁ + L₂

• para $0\leq x\leq L_{1}$ : $y={xR_{1} \over L_{1}}$

la mitad del ángulo:

$\phi _{1}=\arctan({R_{1} \over L_{1}})$ y $y=x\tan(\phi _{1})$

• para $L_{1}\leq x\leq L$ : $y=R_{1}+{(x-L_{1})(R_{2}-R_{1}) \over L_{2}}$

la mitad del ángulo:

$\phi _{2}=\arctan \left({R_{2}-R_{1} \over L_{2}}\right)$ y $y=R_{1}+(x-L_{1})\tan(\phi _{2})$

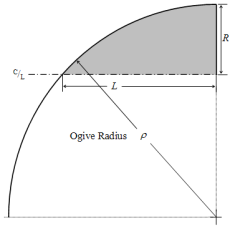
Ojiva tangente

Junto con la forma cónica, la ojiva tangente es la forma más utilizado en la cohetería amateur. El perfil de esta figura está formada por un segmento de un círculo tal que el cuerpo del cohete sea tangente a la curva de la cono de morro en su base, y siendo la base el radio del círculo. La popularidad de esta forma es en gran parte debido a su facilidad de construcción.

El radio del círculo que forma la ojiva se llama radio de ojiva, $\rho$, y está relacionado con la longitud y el radio de la base del cono de morro como se expresa por la fórmula:

$\rho ={R^{2}+L^{2} \over 2R}$

El radio y en cualquier punto x, con x que varía de 0 a L es:

$y={\sqrt {\rho ^{2}-(L-x)^{2}}}+R-\rho$

La longitud, L, debe ser menor o igual a $\rho$. Si son iguales, entonces la forma es un esfera.

Ojiva tangente con punta esférica

A un cono de morro con ojiva tangente normalmente se le añade un segmento de una esfera en la punta. El punto de tangencia entre la esfera y la ojiva tangente se puede encontrar a partir de:

${\begin{aligned}x_{o}&=L-{\sqrt {\left(\rho -r_{n}\right)^{2}-(\rho -R)^{2}}}\\y_{t}&={\frac {r_{n}(\rho -R)}{\rho -r_{n}}}\\x_{t}&=x_{o}-{\sqrt {r_{n}^{2}-y_{t}^{2}}}\end{aligned}}$

donde:

$r_{n}$ es el radio y $x_{0}$ es el centro de la punta esférica.

Y el vértice se puede encontrar a partir de:

$x_{a}=x_{o}-r_{n}$

Ojiva secante

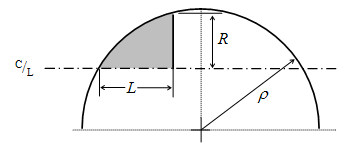
El perfil de esta forma también está formado por un segmento de un círculo, pero la base de la forma no es el radio del círculo definido por el radio de la ojiva. El cuerpo del cohete no será tangente a la curva del cono de morro en su base. El radio de ojiva $\rho$ no está determinado por R y L (como lo es para una ojiva tangente), sino que es uno de los factores a ser elegido para definir la forma del cono de morro. Si el radio de ojiva elegido de una ojiva secante es mayor que el radio de ojiva de una ojiva tangente con el mismo R y L, entonces el resultado es una ojiva secante que se corresponde a una ojiva tangente con una porción de la base truncada.

$\rho >{R^{2}+L^{2} \over 2R}$ y $\alpha =\arctan \left({R \over L}\right)-\arccos \left({{\sqrt {L^{2}+R^{2}}} \over 2\rho }\right)$

Por lo que, el radio y en cualquier punto x, con x desde 0 a L es:

$y={\sqrt {\rho ^{2}-(\rho \cos(\alpha )-x)^{2}}}+\rho \sin(\alpha )$

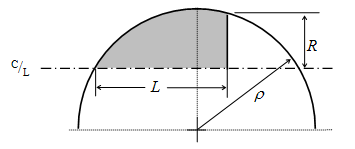
Si el $\rho$ es menor al de la ojiva tangente $\rho$, entonces el resultado será una ojiva secante que sobresale con un diámetro máximo que es mayor al diámetro de la base. El ejemplo clásico de esta forma es el cono de morro del Honest John. También, la selección del radio de ojiva debe de ser mayor que la mitad de la longitud del cono de morro.

${\frac {L}{2}}<\rho <{R^{2}+L^{2} \over 2R}$

Elíptico

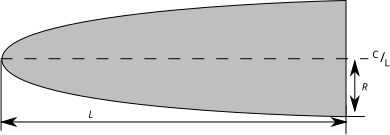
El perfil de esta forma, es la mitad de una elipse, con su eje principal como la línea central, y el eje menor, siendo la base del cono de morro. La rotación de una elipse completa sobre su eje mayor se conoce como una esferoide prolato, de forma que un cono de morro elíptico podría ser nombrado también como un esferoide prolato. Esta forma es muy popular en vuelo subsónico, como en la cohetería amateur. Esta no es una forma que normalmente se encuentre en ámbito profesional, que casi siempre va a mucha mayor velocidad donde otros diseños son los más adecuados. Si R es igual a L, tenemos un esfera.

$y=R{\sqrt {1-{x^{2} \over L^{2}}}}$

Parabólico

Esta forma no es la que comúnmente se prevé cuando la gente se refiere a un cono de morro "parabólico". La serie parabólica se genera por la rotación de un segmento de parábola en torno a una línea paralela a su latus rectum. Esta construcción es similar a la de la ojiva tangente, excepto que se utiliza una parábola para la definición de la forma en lugar de un círculo. Tal como lo hace en una ojiva, esta construcción produce una forma de cono de morro con una punta afilada. Para la forma típicamente asociada con un cono de morro parabólico, ver las series exponenciales a continuación. (La forma parabólica también se confunde a menudo con la forma elíptica.)

Para $0\leq K'\leq 1$ : $y=R\left({2\left({x \over L}\right)-K'\left({x \over L}\right)^{2} \over 2-K'}\right)$

K' puede variar entre 0 y 1, pero los valores más comunes utilizados son:

K' = 0 para un cono

K' = 0.5 para 1/2 de parábola

K' = 0,75 para un 3/4 de parábola

K' = 1, para toda una parábola

Para el caso de una parábola completa (K' = 1) la forma es tangente al cuerpo en su base, y la base está en el eje de la parábola. Los valores de K' menores a uno resultan en una forma más esbelta, cuya apariencia es similar a la de la ojiva secante. La forma no es tangente a la base, y la base es paralela, pero desplazada del eje de la parábola.

Serie exponencial

Las series exponenciales incluyen la forma que comúnmente se conoce como cono de morro "parabólico", pero la forma correcta de un cono de morro parabólico es un miembro de la serie parabólica (descrito anteriormente). La serie exponencial se caracteriza por su (por lo general) de punta roma, y por el hecho de que su base no es tangente al cuerpo. Siempre hay una discontinuidad en la unión entre el cono de morro y el cuerpo. La forma puede ser modificada en base a suavizar esta discontinuidad. Tanto un cilindro, como un cono son formas que son miembros de esta serie.

El exponente de la serie se genera por la rotación de la curva y = R(x/L)ⁿ sobre el eje x para valores de n menores que 1. El factor n controla forma de la punta. Para valores de n por encima de 0,7, la punta es bastante afilidada. Conforme n disminuye hacia cero, la forma se vuelve cada vez más roma.

Gráficos que ilustran las formas de la serie exponencial

Para  $0\leq n\leq 1:y=R\left({x \over L}\right)^{n}$

Donde:

n = 1 para un cono

n = 0.75
n = 0.5 para una parábola

n = 0 para un cilindro

Serie de Haack

A diferencia de las anteriores, la serie de Haack no se construye a partir de figuras geométricas. Las formas son, en su lugar, derivadas matemáticamente con el propósito de minimizar el arrastre. La serie es un conjunto continuo de formas que se determinan por el valor de C de las ecuaciones siguientes, dos valores de C tienen un significado especial: cuando C = 0, la notación LD significa la mínima resistencia para una longitud y diámetro determiandos, y cuando C = 1/3, LV indica la mínima resistencia para una longitud y volumen determinados. La series de Haack no son perfectamente tangente al cuerpo en su base, excepto para el caso en que C = 2/3. Sin embargo, la discontinuidad es generalmente tan leve como para ser imperceptible. Para C > 2/3, la serie de Haack crecen hasta un diámetro mayor que el diámetro de la base. La punta de la serie de Haack no llegan a un punto afilado, son ligeramente redondeadas.

Gráficos que ilustran las series de Haack

${\begin{aligned}\theta &=\arccos \left(1-{2x \over L}\right)\\y&={R \over {\sqrt {\pi }}}{\sqrt {\theta -{\sin(2\theta ) \over 2}+C\sin ^{3}(\theta )}}\end{aligned}}$

Donde:

C = 1/3 para LV-Haack

C = 0 para LD-Haack

Von Kármán

La serie de Haack dando un arrastre mínimo para la longitud y el diámetro, el LD-Haack donde C=0, se llama comúnmente la de Von Kármán.

Características del arrastre del cono de morro

Para aviones y cohetes, por debajo de 0.8 Mach, la resistencia de presión del cono de morro es prácticamente cero para todas las formas. El factor más importante es la resistencia de fricción, que depende en gran parte del área mojada, la suavidad de la superficie en esa zona, y la presencia de las discontinuidades en la forma. Por ejemplo, en cohetes subsónicos cohetes una corta, roma y suave forma elíptica es generalmente la mejor. En la región transónica y posterior, donde la resistencia de presión aumenta drásticamente, el efecto de la forma del cono de morro en la resistencia se vuelve muy importante. Los factores que influyen en la resistencia de presión son por lo general la forma del cono de morro, su relación de "fineness", y su relación de "bluffness".

Influencia de la forma general

Vista de cerca de un cono de morro en un avión de pasajeros

Muchas referencias en el diseño del cono de morro contienen datos empíricos comparando la resistencia producida por diferentes formas del cono de morro en diferentes regímenes. El gráfico que se muestra aquí parece ser la más completa y útil recopilación de datos para los regímenes de vuelo de mayor interés. Este gráfico en general está de acuerdo con la más detallada, pero menos completa recopilación de datos que se encuentran en otras referencias (especialmente los de la USAF Datcom).

Comparación de la resistencia de las diversas formas de cono de morro para diferentes valores de Mach. Las clasificaciones son: superior (1), bueno (2), regular (3), inferior (4).

En la mayoría de los diseños, la mayor preocupación es el rendimiento de vuelo en la región de 0,8 a 1,2 Mach. Aunque los datos no están disponibles para muchas formas en esta región, la gráfica claramente sugiere que, o bien la de Von Kármán, o la serie exponencial con n = 1/2, serían preferibles a la popular cónica u ojiva, para este propósito.

F-16 Fighting Falcon

Esta observación va en contra de lo que a menudo se piensa de que un cono de morro cónico es mejor para velocidades transónicas y supersónicas. Los aviones de combate probablemente son buenos ejemplos de conos de morro optimizados para la región transónica, a pesar de que su forma de morro es a menudo distorsionada por otras consideraciones de aviónica. Por ejemplo, el morro de un F-16 Fighting Falcon parece ser muy próximao a una de Von Kármán.

Influencia de la relación de finura

La relación entre la longitud del cono y su diámetro base es conocida como la relación de finura. A veces, también se conoce como relación de aspecto, a pesar de que este término se aplica generalmente a las alas. La relación de finura a menudo se aplica a la totalidad del vehículo, teniendo en cuenta la longitud total y diámetro.

A velocidades supersónicas, la relación de finura tiene un efecto significativo sobre la resistencia de onda producida, especialmente a bajos ratios; pero hay muy poca ganancia adicional para ratios de más de 5:1. Al aumentar la relación de finura, el área mojada, y por lo tanto la resistencia de fricción, también va a aumentar. Por lo tanto, la relación de finura con menor arrastre va a ser enfrentamiento entre disminuir la resistencia de onda y aumentar la resistencia de fricción.

Referencias

• Gary A. Crowell Sr. «The Descriptive Geometry Of Nose Cones». Archivado desde el original el 11 de abril de 2011. Consultado el 11 de abril de 2011. 
• «Nose cones equations». Nose Cones excel sheet by Kemal Payza. Archivado desde el original el 28 de abril de 2018. Consultado el 11 de mayo de 2018. 
• Department of Defense Military Design Handbook (1990). Design of Aerodynamically Stabilized Free Rockets. U.S. Army Missile Command. MIL-HDBK-762(MI). [1]
• Geschoßformen kleinsten Wellenwiderstandes by W. Haack, Bericht 139 der Lilienthal-Gesellschaft (1941)
• Chin SS. (1961). Missile Configuration Design. McGraw-Hill Book Co., Inc., New York. 

• Datos: Q2875693
• Multimedia: Nose cone design (fluid dynamics) / Q2875693