Tangente (trigonometría)

Tangente
Gráfica de Tangente
Definición	tg x
Dominio	$\mathbb {R} \setminus \left\{{\frac {\pi }{2}}+n\pi \right\},\;n\in \mathbb {Z}$
Imagen	$\mathbb {R}$
Cálculo infinitesimal
Derivada	$\sec ^{2}x$
Función inversa	arctan x

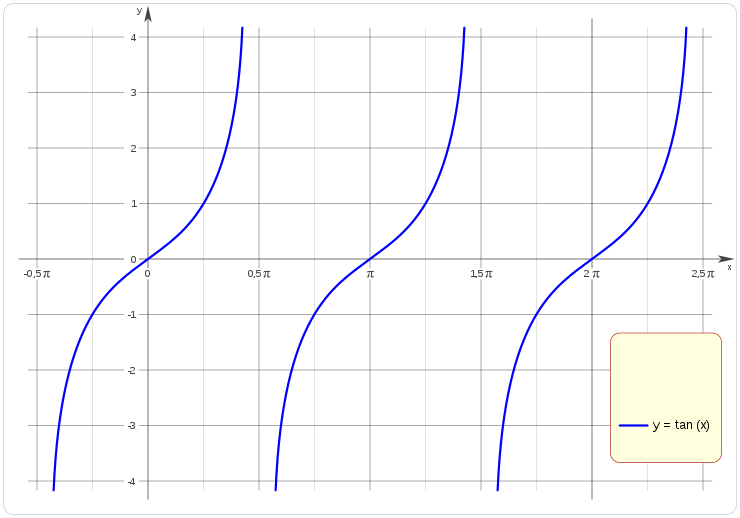
En matemática, la tangente es una función impar y es una función periódica de periodo $\pi$ con indeterminaciones en ${\frac {\pi }{2}}+n\pi ,\;n\in \mathbb {Z}$, y además una función trascendente de variable real. Su nombre se abrevia de las dos siguientes formas: tan y tg.​

$\operatorname {tg} \;x=-\operatorname {tg} (-x)$

$\operatorname {tg} \;x=\operatorname {tg} (\pi +x)$

En trigonometría, la tangente de un ángulo (de un triángulo rectángulo) se define como la razón entre el cateto opuesto y el adyacente:

$\operatorname {tg} \alpha ={\frac {a}{b}}={\frac {BC}{OC}}$

Esta razón no depende del tamaño del triángulo rectángulo escogido sino que es una función dependiente del ángulo $\alpha .$

Esta construcción permite representar el valor del tangente para ángulos no agudos.

Semejanza

Dada la circunferencia de radio 1 y una recta r que pasa por el centro, describe un triángulo rectángulo con ángulo $\alpha$ como en la imagen, y tenemos las siguientes relaciones por semejanzas:

$\operatorname {tg} \alpha ={\frac {CB}{AC}}={\frac {DE}{AD}}={\frac {DE}{1}}=DE$

El segmento $DE$ representa el valor de la tangente de $\alpha .$

Representación gráfica

Identidades

Tangente de la suma de dos ángulos

Esta identidad trigonométrica parte de la identidad de la suma de dos ángulos ya conocida para el seno y el coseno.

• Dados los ángulos $\phi ,\theta \$:

$\operatorname {tg} \left(\phi +\theta \right)={\cfrac {\operatorname {sen}(\phi +\theta )}{\cos(\phi +\theta )}}$

• Reemplazando por las identidades antes mencionadas:

$\operatorname {tg} \left(\phi +\theta \right)={\cfrac {\operatorname {sen} \phi \cos \theta +\cos \phi \operatorname {sen} \theta }{\cos \phi \cos \theta -\operatorname {sen} \phi \operatorname {sen} \theta }}$

• Dividiendo al numerador y al denominador por $\cos \phi \cos \theta \,$:

$\operatorname {tg} \left(\phi +\theta \right)={\cfrac {\cfrac {\operatorname {sen} \phi \cos \theta +\cos \phi \operatorname {sen} \theta }{\cos \phi \cos \theta }}{\cfrac {\cos \phi \cos \theta -\operatorname {sen} \phi \operatorname {sen} \theta }{\cos \phi \cos \theta }}}$

• Separando la suma y la resta:

Tangente de la diferencia de dos ángulos

• $\operatorname {tg} \left(\phi +(-\theta )\right)={\frac {\operatorname {tg} \phi +\operatorname {tg} (-\theta )}{1-\operatorname {tg} \phi \operatorname {tg} (-\theta )}}$

• Al ser una función impar, se obtiene:

$\operatorname {tg} \left(\phi -\theta \right)={\frac {\operatorname {tg} \phi -\operatorname {tg} \theta }{1+\operatorname {tg} \phi \operatorname {tg} \theta }}$

Fórmula resumida

$\operatorname {tg} \left(\phi \pm \theta \right)={\frac {\operatorname {tg} \phi \pm \operatorname {tg} \theta }{1\mp \operatorname {tg} \phi \operatorname {tg} \theta }}$

Tangente del ángulo doble

Partiendo de

$\operatorname {tg} \left(\phi +\theta \right)={\frac {\operatorname {tg} \phi +\operatorname {tg} \theta }{1-\operatorname {tg} \phi \operatorname {tg} \theta }}$

y haciendo $\phi =\theta \,$ entonces:

$\operatorname {tg} \left(2\phi \right)={\frac {2\operatorname {tg} \phi }{1-\operatorname {tg} ^{2}\phi }}$

Tangente del ángulo triple

Conociendo la tangente del ángulo ψ, hallar la tangente de 3ψ

$\operatorname {tg} \left(3\psi \right)={\frac {3\operatorname {tg} \psi -\operatorname {tg} ^{3}\psi }{1-3\operatorname {tg} ^{2}\psi }}$

Tangente del ángulo mitad

Se trata de hallar la tangente de la mitad de θ, conociendo los de θ:

$\operatorname {tg} {\frac {\theta }{2}}={\frac {\operatorname {sen} \theta }{1+\cos \theta }}$ ​

Derivada de la tangente

$[\operatorname {tg} (x)]'=\sec ^{2}(x)\,$

Véase también

• Función impar
• Trigonometría

Enlaces externos

• Weisstein, Eric W. «Tangente». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 

• Datos: Q1129196
• Multimedia: Tangent function / Q1129196