Notación científica
La notación científica, también denominada notación exponencial, es una forma de escribir los números basada en potencias de 10,[1] lo que resulta especialmente útil para la representación de valores muy grandes o pequeños, así como para el cálculo con ellos. Esto es particularmente cierto en física y química en que estos valores son frecuentes, por lo que esta notación resulta adecuada para mostrar claramente las cifras significativas y permitir inmediatas comparaciones de magnitud.[2][3][4] Por ejemplo, en valores aproximados:
- masa del electrón
0.000 000 000 000 000 000 000 000 000 000 911 = 9.11 × 10-31 kg - constante de Avogadro (cantidad de materia: mol[5])
602 000 000 000 000 000 000 000 = 6.02 × 1023 entidades elementales - mayor distancia observable del universo:
740 000 000 000 000 000 000 000 000 m = 7.4 × 1026 m[6] - masa del protón:
0.000 000 000 000 000 000 000 000 001 67 kg = 1.67 × 10-27 kg[7]
El exponente indica los lugares que debe desplazarse la coma para pasar de notación científica a notación decimal: a la derecha si es positivo y hacia la izquierda si es negativo. Cuando se trata de convertir un número a notación científica el proceso es a la inversa.[8]
Mantisa y orden de magnitud[editar]

La notación científica de un número[9][10][11] es de la forma , donde:
- La «mantisa» m es un número decimal cuya parte entera tiene una sola cifra distinta de cero.
- El «orden de magnitud» es una potencia de exponente entero.
Así:
- 520 = 5.2 × 102
- -45.9 = -4.59 × 101
- 575 230 000 000 000 = 5.7523 × 1014
- 0.0523 = 5.23 x 10-2
- 0.000 000 000 000 000 690 3 = 6.903 × 10−16
Historia[editar]

El primer intento de representar números demasiado grandes fue emprendido por el matemático y filósofo griego Arquímedes,[12] y descrita en su obra El contador de arena,[13] en el siglo III a. C. Él desarrolló un sistema de representación numérica para estimar un límite superior para el número de granos de arena necesarios para llenar el universo. Para hacer esto tuvo que estimar el tamaño del universo según el modelo vigente en ese momento y, además, buscar una manera de expresar números muy grandes. El número estimado por él era de 1063 gramos.[14][15]
Hay quien piensa, Rey Gelón, que el número de granos de arena es infinito. Y cuando menciono arena no me refiero solo a aquella que existe en Siracusa y en el resto de Sicilia, sino también la que se encuentra en otras áreas, sean ellas habitadas o deshabitadas. Una vez más, hay quienes, sin considerarlo infinito, piensan que ningún número fue nombrado todavía que sea suficientemente grande para exceder su multiplicidad. Y es claro que aquellos que tienen esta opinión, si imaginasen una masa arena del tamaño de la masa de la Tierra, incluyendo en esta todos mares y depresiones de la Tierra llenas hasta una altura igual a la más alta de las montañas, sería mucho aún para reconocer que cualquier número puede expresarse de tal manera que superar la multiplicidad de arena allí existente. Pero voy a tratar de mostrar por medio de demostraciones geométricas que conseguiréis acompañar que, dos números nombrados por mí y que constan en el trabajo que envié a Zeuxipo, algunos exceden, no solo el número de masa de arena igual en magnitud a la de la Tierra rellena de manera que se describe arriba, sino también la masa igual en magnitud a la del universo.El contador de Arena (Arquímedes), pg. 1[13]
Fue a través de la notación científica que se concibió el modelo de representación de los números reales mediante coma flotante.[16] Esa idea fue propuesta por Leonardo Torres y Quevedo (1914), Konrad Zuse (1936) y George Robert Stibitz (1939).[12] La codificación en punto flotante de los ordenadores actuales es básicamente una notación científica de base 2.[17]
La programación con el uso de números en notación científica consagró una representación sin superíndices, en el cual la letra e (o E) a mantisa del exponente mantisa. Por lo tanto, 1.785 × 105 e 2.36 × 10−14 se representan, respectivamente, con 1.785E5 y 2.36E-14 (como la mayoría de los lenguajes de programación están basados en inglés, las comas son sustituidas por puntos).[12]
Tipos de notación científica[editar]
En la notación científica estándar, el exponente e es elegido de manera que el valor absoluto de m permanezca al menos uno pero menos de diez (1 ≤ | m | <10). Por ejemplo, 350 se escribe como 3.5 × 10². Esta forma permite una comparación simple de dos números del mismo signo en m, como el exponente e indica el número de la orden de grandeza. En notación estándar el exponente e es negativo para un número absoluto con valor entre 0 y 1 (por ejemplo, menos de la mitad es -5 × 10−1). El 10 y el exponente son generalmente omitidos cuando el exponente es 0.[18]
En muchas áreas, la notación científica se normaliza de esta manera, a excepción de los cálculos intermedios, o cuando una forma no estándar, tales como la notación de ingeniería, se desea. La notación científica (normalizada) suele llamarse notación exponencial - aunque este último término es más general y también se aplica cuando m no está restringido al intervalo de 1 a 10 (como en la notación de ingeniería, por ejemplo) y para otras bases distintas de 10 (como en 315 × 220).[19]
Notación Exponencial. (Notación E)[editar]
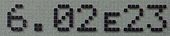
La mayoría de calculadoras y programas informáticos están programados para mostrar en notación científica los números excesivamente grandes o pequeños. Pese a esto, por lo general no son capaces de ilustrar "a la manera tradicional" los exponentes de potencias, como por ejemplo 107 (lo mismo ocurre con los subíndices matemáticos). En estos casos recurren a un formato alternativo de representación gráfica de potencias: la notación E, donde la letra E, seguida de un número, representa, literalmente, «multiplicado por diez elevado a» (es decir, "× 10n"). Dicho de otro modo, si tomamos dos números reales m y n, la representación "mEn" significaría exactamente m × 10n.
El carácter e no tiene nada que ver con la constante matemática e (la confusión no es posible cuando se utiliza la letra mayúscula E); y aunque represente un exponente, la notación se refiere generalmente como notación e (científica) o notación E (científica), en vez de notación exponencial (científica) (aunque este última también puede ocurrir).[20]
Ejemplos[editar]
- En el lenguaje de programación FORTRAN
6.0221415E23es equivalente a 6.022 141 5×1023. - El lenguaje de programación ALGOL 60 usa un subíndice diez en lugar de la letra E, por ejemplo
6.02214151023.[21] ALGOL 68 también permite E minúsculas, por ejemplo 6.0221415e+23.
- El lenguaje de programación ALGOL 68 tiene la opción de 4 caracteres en (eE\⏨). Ejemplos:
6.0221415e23,
6.0221415E23,
6.0221415\23 o
6.0221415⏨23.[22]
6.0221415&23
(o 6.0221415&&23).[23]
- En lenguaje de programación multiparadigma como Python no es relevante la utilización de mayúscula o minúscula para el carácter E o e, teniendo el mismo significado.
6.0221415e23 = 6.0221415E23
Notación de ingeniería[editar]
La notación de ingeniería difiere de la notación científica normalizada en el cual el exponente e está restringido a múltiplos de 3. Por consiguiente, el valor absoluto de m está en el intervalo 1 ≤ |m| <1000, en lugar de 1 ≤ |m| < 10.[24][25] Aunque sea conceptualmente similar, la notación de ingeniería rara vez se la llama notación científica.
Los números de esta forma son fáciles de leer, utilizando los prefijos de magnitud como mega (m = 6), kilo (m = 3), mili (m = −3), micro (m = −6) o nano (m = −9). Por ejemplo, 12.5×10−9 m se puede leer como «doce punto cinco nanómetros» o escrito como 12.5 nm.[24][26]
Motivación[editar]

La notación científica es una forma muy conveniente para escribir números pequeños o grandes y hacer cálculos con ellos. También transmite rápidamente dos propiedades de una medida que son útiles para los científicos, las cifras significativas y orden de magnitud. Escribir en notación científica le permite a una persona eliminar ceros delante o detrás de las cifras significativas. Esto es muy útil para mediciones muy grandes o muy pequeñas en astronomía y en el estudio de moléculas.[3] Los siguientes ejemplos pueden demostrarlo.
Ejemplos[editar]
- La masa de un electrón es aproximadamente 0.000 000 000 000 000 000 000 000 000 000 910 938 22 kg. En notación científica, esto se escribe 9.109 382 2×10-31 kg.[7]
- La masa de la tierra es de alrededor de 5 973 600 000 000 000 000 000 000 kg. En notación científica, este valor está representado por 5.9736x1024 kg.[27]
- La circunferencia de la Tierra es de aproximadamente 40 000 000 m. En notación científica queda 4×107 m. En notación de ingeniería, es de 40×106 m. En el estilo de representación del SI, puede ser escrita 40 Mm (40 megámetro).[28]
Cifra significativa[editar]
Una ventaja de la notación científica es que reduce la ambigüedad del número de dígitos significativos. Todos los dígitos en notación científica estándar son significativos por convención. Pero, en notación decimal cualquier cero o una serie de ceros al lado del punto decimal son ambiguos, y puede o no indicar números significativos (cuando ellos deben estar subrayados para hacer explícitos que ellos son ceros significativos). En una notación decimal, los ceros al lado del punto decimal no son, necesariamente, un número significativo. Es decir, pueden estar allí solo para mostrar dónde está el punto decimal. Sin embargo, en notación científica se resuelve esta ambigüedad, porque los ceros que se muestran son considerados significativos por convención.[29] Por ejemplo, usando la notación científica, la velocidad de la luz en unidades del SI es 2.99792458×108 m/s y la eminencia es 2,54×10−2 m; ambos números son exactos, por definición, las unidades «pulgadas» por centímetro y m en términos de la velocidad de la luz.[30] En estos casos, todas las cifras son significativas. Se puede adicionar un único cero o cualquier número de ceros al lado derecho para mostrar más dígitos significativos, o un único cero con una barra en la parte superior se puede agregar a mostrar infinitos dígitos significativos (así como en notación decimal).
Ambigüedad del último dígito en notación científica[editar]
Es habitual en mediciones científicas registrar todos los dígitos significativos de las mediciones, y asumir un dígito adicional, si hubiera cierta información a todos los disponibles para el observador a hacer una suposición. El número resultante es considerado más valioso del que sería sin ese dato extra, y es considerado una cifra significativa, ya que contiene alguna información que conduce a una mayor precisión en las mediciones y en la agregación de las mediciones (agregarlas o multiplicarlas).
A través de anotaciones adicionales, se puede transmitir información adicional sobre la exactitud. En algunos casos, puede ser útil saber que es el último algoritmo significativo. Por ejemplo, el valor aceptado de la unidad de carga elemental puede ser válidamente expresado como 1.602176487(40)×10−19 C,[31] y cuyas cifras aparecen entre paréntesis al final del valor, indican su incertidumbre, específicamente se expresa como 0.000000040×10−19 C, y es un acceso directo a la abreviatura de (1.602176487 ± 0.000000040)×10−19 C.
Orden de magnitud[editar]
La notación científica permite una rápida comparación entre varias cantidades homogéneas. Por ejemplo:
Para compararlas con suficiente aproximación basta el cociente entre las potencias de diez:
Es decir, el protón es aproximadamente cuatro órdenes de magnitud (alrededor de 10 000 veces) más masivo que el electrón.[32]
Descripción[editar]

En sentido amplio, la notación científica permitiría una infinidad de representaciones de cada valor. Por ejemplo, para 739 000 000 000 tendríamos, entre muchas otras, las siguientes:
- 739×109 = 73.9×1010 = 7.39×1011
Sin embargo, se exige que la mantisa o coeficiente sea mayor o igual a 1 y menor que 10.[12] De ese modo tenemos una forma única de notación científica:
- 739 000 000 000 = 7.39×1011
Cómo transformar[editar]
Para transformar cualquier número a la notación científica debemos mover la coma obedeciendo al principio de equilibrio.[cita requerida]
Tomemos el ejemplo a continuación:
La notación científica requiere que la mantisa (coeficiente) es de entre 1 y 10 en valor absoluto. En esta situación, el valor apropiado sería 2,5375642 (observe que la secuencia de números es la misma, solamente cambia la posición de la coma). Para el exponente, pena el principio de equilibrio: «Cada decimal que disminuye el valor de mantisa aumenta el exponente en una unidad, y viceversa».
En este caso, el exponente es 5.
Observe la transformación paso a paso:
Otro ejemplo, con valores por debajo de 1:
0.0000000475
0.000000475 × 10−1
0.00000475 × 10−2
0.0000475 × 10−3
0.000475 × 10−4
0.00475 × 10−5
0.0475 × 10−6
0.475 × 10−7
4.75 × 10−8
Uso de espacios[editar]
En notación científica, en notación E y la notación de ingeniería, el espacio (el que, en formato de texto, puede ser representado por un espacio normal de ancho o por un espacio delgado), solo se permite antes y después de ×, en frente de E o e puede ser omitido, aunque sea menos común que lo haga antes del carácter alfabético.[35]
Operaciones matemáticas con notación científica[editar]
Adición y sustracción[editar]
Para sumar o restar dos números en notación científica, es necesario que los exponentes sean los mismos. Es decir, uno de los valores debe ser transformado para que su exponente sea igual al del otro. El resultado probablemente no estará en la forma exigida (mantisa con una sola cifra distinta a 0 a la izquierda de la coma) por lo que será convertido posteriormente.[37]
Ejemplos:
=
=
Multiplicación[editar]
Multiplicar las mantisas y sumar los exponentes de cada valor.[37]
Ejemplo:
=
División[editar]
Dividir las mantisas y restar los exponentes de cada valor:[37]
Ejemplos:
=
Exponenciación o Potenciación[editar]
La mantisa es elevada al exponente externo y el exponente de base diez se multiplica por el exponente externo.[37]
Radicación[editar]
Antes de realizar la radicación es necesario transformar un exponente a un múltiplo del índice. Después de que se hace esto, el resultado es la radicación de la mantisa multiplicada por diez elevado a la relación entre el exponente y el índice de radical.[37]
[38]
Véase también[editar]
Referencias[editar]
- ↑ Efeito Joule. «Potência de diez e Notação científica» (en portugués). Consultado el 7 de noviembre de 2009.
- ↑ Chem. «Notación científica». Math Skills review (en inglés). Consultado el 31 de mayo de 2009.
- ↑ a b qfojo.net. «¿Cuál es la notación científica y cómo se puede usar?». Potencias (en portugués). Archivado desde el original el 17 de febrero de 2010. Consultado el 7 de noviembre de 2009.
- ↑ Só matemática. «Letra "N"». Dicionário de matemática (en portugués). Consultado el 29 de mayo de 2009.
- ↑ UOL. «Notação científica - Potência de 10 simplifica cálculos» (en portugués). Archivado desde el original el 9 de noviembre de 2009. Consultado el 24 de febrero de 2009.
- ↑ ScienceBlogs - 100nexos. «Bicicletas e universo observável» (en portugués). Archivado desde el original el 2 de junio de 2020. Consultado el 21 de abril de 2009.
- ↑ a b Irineu Gomes Varella (2004). «Constantes físicas». Tabelas e dados astronômicos (en portugués). Uranometria Nova. Archivado desde el original el 28 de abril de 2009. Consultado el 21 de abril de 2009.
- ↑ Skoog, Douglas A.; West, Donald M.; Holler, F. James (1997). Fundamentos de química analítica. Reverte. ISBN 9788429175554. Consultado el 19 de febrero de 2018.
- ↑ Spiegel, Murray R. «Teoría y problemas de álgebra». En Bookman, ed. 2004 (en portugués) (2 edición). p. 62. ISBN 85-363-0340-9. Consultado el 17 de noviembre de 2009.
- ↑ «Mathway | Solucionador de problemas de matemáticas». www.mathway.com. Consultado el 19 de febrero de 2018.
- ↑ «Notación científica, ejercicios resueltos».
- ↑ a b c d e Ebah. «Notação científica ? Exponenciação - Radiciação» (en portugués). Archivado desde el original el 29 de abril de 2011. Consultado el 20 de abril de 2009.
- ↑ a b Departamento de educação da Universidade de Lisboa. «O Contador de Areia». Tradução feita pela Universidade de Lisboa (en portugués). Archivado desde el original el 23 de noviembre de 2008. Consultado el 22 de abril de 2009.
- ↑ Departamento de educação da Universidade de Lisboa. «Arquimedes» (en portugués). Archivado desde el original el 22 de abril de 2009. Consultado el 21 de abril de 2009.
- ↑ BARCO, Luiz. «Você sabe escrever um bilhão?» (en portugués). Super Interessante. Consultado el 7 de enero de 2011.
- ↑ UFPR - Universidade Federal do Paraná (20 de abril de 2009). «Representação de números reais (ponto flutuante)». Departamento de informática (en portugués). Archivado desde el original el 25 de diciembre de 2009. Consultado el 22 de abril de 2009.
- ↑ Marcos Paz. «Codificação» (pdf). Utilização de códigos em sistemas de comunicação (en portugués). Consultado el 22 de abril de 2009. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- ↑ Universidade Federal do Rio Grande do Norte. «Operações com Ponto Flutuante» (en portugués). Archivado desde el original el 25 de octubre de 2008. Consultado el 29 de mayo de 2009.
- ↑ Unesp. «Notação científica» (ppt) (en portugués). Archivado desde el original el 5 de diciembre de 2011. Consultado el 29 de mayo de 2009.
- ↑ childrens-mercy. «E notation» (asp) (en inglés). Archivado desde el original el 14 de octubre de 2009. Consultado el 20 de setiembre de 2009.
- ↑ Informe sobre la Algorithmic Language ALGOL 60, Ed. P. Naur, Copenhage 1960
- ↑ «Revised Report on the Algorithmic Language Algol 68» (en inglés). Setiembre de 1973. Consultado el 30 de abril de 2007.
- ↑ «SIMULA Standard As defined by the SIMULA Standards Group - 3.1 Numbers» (en inglés). Agosto de 1986. Consultado el 6 de octubre de 2009.
- ↑ a b «A really simple way to do Scientific and Engineering Notation, that always gives you the right answer» (html). eskimo.com (en inglés). Archivado desde el original el 12 de septiembre de 2009. Consultado el 11 de octubre de 2009.
- ↑ Professor Osvaldo Venezuela. Mecânica MÓDULO 1 – Introdução (pdf). «Algarismos Significativos». Mackenzie (en portugués). Archivado desde el original el 2 de abril de 2015. Consultado el 11 de octubre de 2009.
- ↑ «Engineering Notation». Tclers Wiki (en inglés). 12 de diciembre de 2007. Consultado el 11 de octubre de 2009.
- ↑ «Estatísticas da Terra» (en portugués). Universidade Federal do Rio Grande do Sul. Consultado el 27 de octubre de 2009.
- ↑ «Nosso Planeta Terra» (en portugués). Ache Tudo e Região. Consultado el 27 de octubre de 2009.
- ↑ Química i. EUNED. ISBN 9789968316262. Consultado el 19 de febrero de 2018.
- ↑ «NIST value for the speed of light» (en inglés).
- ↑ «NIST value for the elementary charge» (en portugués). Consultado el 28 de mayo de 2015.
- ↑ Site do Movimento Sindical. «Átomo». A energia nuclear - Conceitos e definições. Archivado desde el original el 5 de abril de 2010. Consultado el 7 de noviembre de 2009.
- ↑ Departamento de Astronomia do Instituto de Física da UFRGS. «Massa da Via-Láctea» (en portugués). Consultado el 22 de abril de 2009.
- ↑ Física.net. «Conceito de mol». Archivado desde el original el 3 de marzo de 2016. Consultado el 22 de abril de 2009.
- ↑ Muestras de uso de la terminología y variantes (En inglés): [1], [2], [3], [4], Archivado el 29 de octubre de 2006 en Wayback Machine., [5]
- ↑ Esclerose Múltipla (29 de setiembre de 2006). «Quantos neurônios tem um cérebro?» (en portugués). Consultado el 25 de abril de 2009.
- ↑ a b c d e CEDOM.net. «Notação científica» (en portugués). Consultado el 7 de noviembre de 2009. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- ↑ O site da Educação. «Cálculos de notação científica» (en portugués). Archivado desde el original el 29 de julio de 2013. Consultado el 29 de mayo de 2015.
Enlaces externos[editar]
- Descripción de la notación de Arquímedes (en portugués)
- Esta obra contiene una traducción total derivada de «Notação científica» de Wikipedia en portugués, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.






















![{\displaystyle {\sqrt[{5}]{6.7\cdot 10^{17}}}={\sqrt[{5}]{670\cdot 10^{15}}}={\sqrt[{5}]{670}}\cdot 10^{15/5}\approx 3.674\cdot 10^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6788015ce71c046e6a5ab218bb73307c1d797e9c)