Función periódica
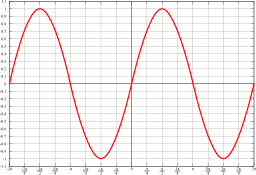

En matemática, una función es periódica si verifica la condición ; el número se llama periodo de la función. Generalmente, se llama periodo fundamental al menor número real positivo T que satisface la condición. Las funciones trigonométricas son ejemplos sencillos de una función periódica, que en combinaciones adecuadas se emplean en el análisis armónico.[1]
De la misma manera, pero en un contexto físico, las ondas periódicas son aquellas ondas que muestran periodicidad respecto del tiempo, es decir, describen ciclos repetitivos. En una onda periódica se cumple:
donde el periodo propio fundamental , es la frecuencia de la componente fundamental de la onda periódica y un número entero.
Toda onda periódica es, por definición, una onda determinista, por cuanto puede ser descrita matemáticamente (mediante un modelo matemático).
Perspectiva general[editar]
La forma más simple de onda periódica es la onda armónica (sinusoidal), que se describe matemáticamente:
Esta onda está completamente caracterizada por tres parámetros: es la amplitud de la sinusoide, es la frecuencia en radianes por segundo (rad/s), y es la fase en radianes. En lugar de , a menudo se utiliza la frecuencia ciclos por segundo o hercios (Hz), donde .

Sin embargo, el modelo descrito para las ondas armónicas no sirve para describir estructuras periódicas más complicadas: las ondas anarmónicas. Joseph Fourier demostró que las ondas periódicas con formas complicadas pueden considerarse como suma de ondas armónicas (cuyas frecuencias son siempre múltiplos enteros de la frecuencia fundamental). Así, supongamos que representa el desplazamiento periódico de una onda en una cierta posición. Si y su derivada son continuas, puede demostrarse que dicha función puede representarse mediante una suma del tipo:
El proceso de determinación matemática de los coeficientes y las constantes de fase , para una forma de onda dada se llama análisis de Fourier. Al igual que una forma de onda periódica puede analizarse como una serie de Fourier mediante las contribuciones relativas de la frecuencia fundamental y los armónicos superiores presentes en la forma de onda, también es posible construir nuevas formas de onda periódicas, sumando a la frecuencia fundamental distintas contribuciones de sus armónicos superiores. Este proceso se denomina síntesis de Fourier.
Es importante notar que para las señales de ancho de banda limitado (en la práctica, todas las de interés en Telecomunicaciones), la suma de armónicos es también finita:
siendo el número total de armónicos de los que se compone la onda periódica. El armónico de frecuencia más baja se denomina primer armónico o armónico de frecuencia fundamental (, por tanto de amplitud , frecuencia y fase ). De hecho, el caso más simple, el de una onda armónica, es un caso particular para un único armónico (). Otros casos requieren un número infinito de armónicos que solo pueden existir en sus formas perfectas como abstracciones matemáticas debido a que en la naturaleza no se pueden crear o transmitir señales de ancho de banda infinito. Sin embargo, incluso sus aproximaciones (descritos como la suma de un número limitado de armónicos) son de gran interés en la práctica, especialmente en Telecomunicaciones. Entre estos casos de señales periódicas compuestos por infinitos armónicos se encuentran las ondas cuadradas (onda compuesta exclusivamente por armónicos impares cuya amplitud es inversamente proporcional al número de armónico, es decir, ) o las triangulares.

Esta propiedad demostrada por Fourier sobre las ondas periódicas es importante en el estudio de la Teoría de la Información y, muy especialmente, en la demostración del Teorema de muestreo de Nyquist-Shannon. Este teorema demuestra que toda onda periódica limitada en banda (limitada a componentes armónicos por debajo de una frecuencia máxima conocida) puede ser descrita en su totalidad y sin ambigüedad por una serie de muestras no cuantificadas si se cumple que la frecuencia de muestreo es superior (nunca igual) al doble de la frecuencia del último armónico que puede contener la onda.
Valores característicos de las ondas periódicas[editar]
Valor medio[editar]
El valor medio de una onda se calcula sobre un intervalo de la función correspondiente a un periodo propio fundamental completo desde cualquier instante .
Es muy frecuente que el valor medio de una onda periódica sea cero. En electrotecnia y electrónica un valor medio no nulo mide la magnitud de un componente de corriente continua en una señal.
Valor eficaz[editar]
El valor eficaz (raíz cuadrática media o RMS) de una onda periódica se calcula sobre un intervalo de la función correspondiente a un periodo propio fundamental completo desde cualquier instante .
El valor eficaz de una onda periódica es de especial interés en física cuando se aplica a presiones (mecánica), tensiones o intensidades (electrotecnia o electrónica) para cálculos relacionados con la energía o la potencia. Con relación al valor máximo (o valor de cresta o pico) en una ónda de valor medio nulo, el cálculo del valor eficaz de las siguientes formas de onda se pueden simplificar:
- Onda armónica simple (sinusoidal):
- Onda cuadrada :
- Onda triangular:
La relación entre la amplitud máxima y el valor eficaz de una onda periódica depende, por tanto, de la forma de onda.
Factor de pico o cresta[editar]
Se define como la relación entre el valor de pico y el valor eficaz. Ejemplos de factores de pico:
- Onda armónica simple (sinusoidal):
- Onda cuadrada:
- Onda triangular:
Ejemplos[editar]
En la vida diaria existen muchos casos de funciones periódicas en que la variable es el tiempo; fenómenos como el movimiento de las manecillas de un reloj o las fases de la luna muestran un comportamiento periódico. Un movimiento periódico es aquel en el que la posición o posiciones del sistema se pueden expresar con arreglo a funciones periódicas, todas con el mismo periodo.
Para una función aplicada al conjunto de los números reales o al de los enteros, significa que la totalidad de su gráfica puede ser representada a partir de copias de una determinada porción de ésta, repetida a intervalos regulares.
De forma más explícita, se dice que una función f es periódica con periodo P mayor que cero si cumple que:
para todos los valores de x en el dominio de f. De manera análoga, una función no periódica es aquella que no posee dicho periodo P.
Un ejemplo sencillo es la función f que devuelve la parte fraccional de su argumento:
Si una función f es periódica con periodo P, entonces para todo x en el dominio de f y para todo n entero:
En el ejemplo anterior, el valor de P es 1, dado que:
Esto no implica que el periodo de una función tenga que recibir el menor valor posible que satisfaga la expresión anterior, sino que podría tomar cualquier otro.
Las funciones trigonométricas, tales como la función seno o coseno, son casos típicos de funciones periódicas, en las que su periodo es de 360 grados. En el caso de la tangente, vemos que su periodo es menor, siendo este de 180 grados.

Véase también[editar]
Referencias[editar]
- ↑ Watson Fulks. Cálculo avanzado. Limusa, impreso en México- 1973
Enlaces externos[editar]
- Lectures on Physics Periodic Waves (inglés).
- Ondas en telecomunicaciones
- Periodic Waves (inglés).
- Formas de onda (español).






















![{\displaystyle x_{a}(t)={\frac {4A}{\pi }}\sum _{n=1}^{\infty }{\frac {1}{2n-1}}\sin[(2n-1)\Omega t+\theta ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dadab69bf165c84ef06a735c2d0898f78f49c9e)
![{\displaystyle x_{a}(t)={\frac {4A}{\pi }}\sum _{n=1}^{25}{\frac {1}{2n-1}}\sin[(2n-1)\Omega t+\pi ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a9857929cc952253e709cd327ad41505428d2a2)














