Valor eficaz

Se denomina valor eficaz al valor cuadrático medio de una magnitud eléctrica. El concepto de valor eficaz se utiliza especialmente para estudiar las formas de onda periódicas, a pesar de ser aplicable a todas las formas de onda, constantes o no. En ocasiones se denomina con el extranjerismo RMS (del inglés, root mean square).
Definición[editar]
El valor eficaz de la intensidad i(t) es el valor cuadrático medio:[1]
donde:
- es el periodo de la señal.
Análogamente, el valor eficaz de la tensión es:
Significado físico[editar]
El significado físico del valor eficaz es designar el valor de una corriente rigurosamente constante que al circular sobre una determinada resistencia óhmica produciría los mismos efectos caloríficos que dicha corriente variable. De este modo, se establece un paralelismo entre cualquier tipo de corriente variable y la corriente continua que simplifica los cálculos con esta última.
En ocasiones es importante conocer la potencia media disipada en una resistencia eléctrica cuando la corriente no es constante. La potencia media disipada es:
Cuando dicha corriente es periódica, y teniendo en cuenta la ley de Ohm:
Que, por la definición de valor eficaz, es igual que:
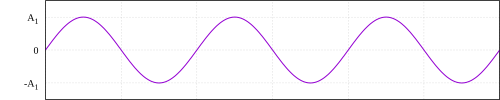
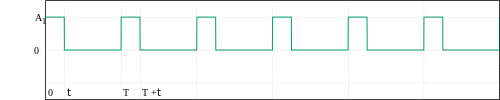
Valor eficaz para formas de onda comunes[editar]
Para formas de onda periódicas donde hay una frecuencia definida, el valor eficaz es independiente de dicha frecuencia.
Nota: Donde D, está expresada en "por unidad" del periodo T (D = t/T).
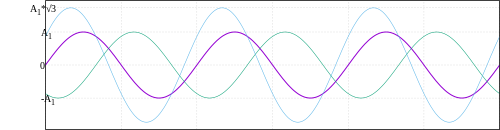
Combinaciones de ondas[editar]
Un caso bastante común es una onda periódica que contiene componente de continua. En ese caso, el valor eficaz es (indistintamente para la tensión o la corriente):
donde es el valor eficaz de la componente continua y es el valor eficaz de la componente alterna.
Generalizando, el valor eficaz de una combinación de ondas, si son ortogonales entre sí, es:
Véase también[editar]
Referencias[editar]
- ↑ Alcalde San Miguel, Pablo (2014). Electrotecnia : Instalaciones eléctricas y automáticas (6ª edición). Madrid: Paraninfo. p. 424. ISBN 9788428398770.