Diferencia entre revisiones de «Teoría de categorías»
Página reemplazada por «Qué pena se me chispoteo». |
m Revertidos los cambios de 190.158.133.244 a la última edición de Manuelt15 |
||
| Línea 1: | Línea 1: | ||
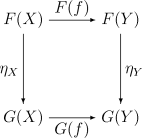
[[Archivo:NaturalTransformation-01.png|thumb|250px|right|Ejemplo de diagrama conmutativo]] |
|||
Qué pena se me chispoteo |
|||
La '''teoría de categorías''' es una teoría [[Matemáticas|matemática]] que trata de forma abstracta con las estructuras matemáticas y sus relaciones. |
|||
La teoría de las categorías fue introducida en [[Topología algebraica]], por [[Samuel Eilenberg]] y [[Saunders MacLane]], en un importante paso para la transición desde [[Homología (matemática)|homología]] (un concepto geométrico intuitivo) a [[Teoría de la homología]] (una materia [[Axioma|axiomática]]). Se ha reclamado que existieron ideas parecidas en la escuela polaca de los años [[1930]] (ver [[Stanislaw Ulam]]). |
|||
Los desarrollos subsiguientes de la teoría fueron impulsados por las necesidades computacionales del [[Álgebra homológica]] y más tarde por las necesidad de axiomáticas en [[Geometría algebraica]], que era el campo más reacio a pasar por el aro de los fundamentos unificadores ''à la'' [[Bertrand Russell|Russell]]-[[Alfred North Whitehead|Whitehead]]. La teoría general -cierta actualización del [[Álgebra universal]] con muchas características nuevas que daban pie a una cierta flexibilidad en semántica y lógicas de orden superior- vino más tarde. |
|||
Las aplicaciones de esta teoría en fundamentos están provocando cierta controversia {{cita requerida}}. |
|||
Estas aplicaciones de categorías en el campo de los fundamentos están siendo trabajadas en bastante detalle y no solamente en matemáticas. Existen matemáticos como [[William Lawvere]] que trabajan en la física, existen físicos trabajando en ''n''-categorías, [[John Baez]], e incluso hay filósofos como [[Alain Badiou]] en Francia o [[Corfield]] en Inglaterra que se han visto obligados a poner sus "indagaciones" bajo las condiciones de la matemática contemporánea. Una idea sobre lo que está pasando se trasluce en algunos escasos libros de texto clásicos en el mundo anglosajón: el "abstract algebra" de ''Birkhoff- Mac Lane'' que después pasa a ser el mismo "abstract algebra" pero de ''Mac Lane-Birkhoff''. |
|||
La [[Lógica Categórica]] es ahora un campo bien definido basado en la [[teoría de tipos]] para la [[Lógica intuicionista]], con aplicaciones a la teoría de la [[programación funcional]] y la [[teoría de dominios]], todas enmarcadas en una [[categoría cartesianamente cerrada]] como descripciones no sintácticas del [[cálculo lambda]]. El uso del lenguaje de la teoría de las categorías le permite a uno aclarar qué tienen exactamente en común todas estas áreas. |
|||
== Categorías == |
|||
Con el concepto de '''categoría''' se pretende capturar -poniendo el énfasis en el concepto de relación, de flecha, más que de elemento y pertenencia- la esencia de una clase de objetos matemáticos, que se relacionan mediante las flechas, los morfismos en la categoría en cuestión. Por ejemplo, la clase de los [[Teoría de grupos|grupos]]. En vez de estudiar los objetos individuales (cada grupo) como se vino haciendo, se enfatizan dichos morfismos entre ellos, que no son otra cosa que las aplicaciones que "conservan su estructura". En el ejemplo de los grupos, dichos morfismos son los [[homomorfismo]]s de grupos. Entonces, una vez que tenemos nuestro "universo categorial" definido -esto es, una categoría- es posible relacionarla con otras categorías mediante [[funtor]]es, que son cierta generalización del concepto de [[función]] para categorías: un funtor asocia a cada objeto de una categoría un objeto de la otra, y a cada flecha de la primera una flecha de la segunda. De cierto modo nos "plasma", nos lleva una imagen de la categoría hacia la otra categoría y con ciertos grados de "afinamiento". Ciertas "construcciones naturales", como el [[grupo fundamental]] de un [[espacio topológico]], pueden ser expresadas como funtores. Además, dichos funtores están muy a menudo naturalmente relacionados y esto lleva al concepto de [[transformación natural]]. |
|||
Históricamente, fue precisamente la motivación de clarificar ciertas [[transformaciones naturales]] en [[Topología algebraica]] lo que sirvió para definir los funtores y las categorías. Y, enseguida, la teoría fue aplicada en [[Álgebra homológica]] y en [[Geometría algebraica]]; ahora se usa en bastantes ramas de la matemática, la física y la filosofía. |
|||
Categorías especiales, como los [[topos]], están sirviendo también como alternativa "generalizadora" y conceptualmente más rica de la [[teoría de conjuntos]] como fundamento de las matemáticas {{cita requerida}}. |
|||
=== Definición === |
|||
Una categoría consiste en: |
|||
* una [[Clase(Teoría de conjuntos)|clase]] de cosas llamadas objetos. (Una clase es "más" que un conjunto, una clase propia no puede ser elemento de ninguna clase). |
|||
* y para cada par de objetos ''A'' y ''B'' un [[conjunto]] Mor(''A'',''B'') de cosas llamadas ''[[morfismo]]s de A a B''. Si ''f'' está en dicho conjunto Mor(''A'',''B''), escribiremos ''f'' : ''A'' → ''B''. |
|||
* para cada tres objetos ''A'', ''B'' y ''C'' hay una operación binaria Mor(''A'',''B'') × Mor(''B'',''C'') → Mor(''A'',''C'') llamada ''composición de morfismos''. La composición de ''f'' : ''A'' → ''B'' y ''g'' : ''B'' → ''C'' se escribe así: ''g'' o ''f'' o bien ''gf''. (Y algunos autores: ''fg''); |
|||
tal que todo ello sigue los siguientes axiomas: |
|||
* (asociatividad) si ''f'' : ''A'' → ''B'', ''g'' : ''B'' → ''C'' y ''h'' : ''C'' → ''D'' entonces ''h'' o (''g'' o ''f'') = (''h'' o ''g'') o ''f'', y |
|||
* (identidad) para cada objeto ''X'' existe un morfismo '''id'''<sub>''X''</sub> : ''X'' → ''X'' llamado ''morfismo identidad en X'', tal que para todo morfismo ''f'' : ''A'' → ''B'' se tiene '''id'''<sub>''B''</sub> o ''f'' = ''f'' = ''f'' o '''id'''<sub>''A''</sub> |
|||
De estos axiomas se puede probar que se tiene sólo un morfismo identidad para cada objeto. |
|||
Si las clases de los objetos y los morfismos son solamente conjuntos, pero no clases, se dice que la categoría es "pequeña" (''small category''). Existen importantes categorías que no lo son. |
|||
=== Ejemplos === |
|||
Cada categoría es presentada en términos de sus objetos y morfismos. |
|||
*La categoría [[Magma (categoría)|'''Mag''']] de todos los [[magma (álgebra)|magmas]] junto con sus [[homomorfismo]]s. |
|||
**La categoría [[Medial (categoría)|'''Med''']] de todos los [[medial (álgebra)|magmas mediales]] junto con sus [[homomorfismo]]s. |
|||
*La cat [[Mon (categoría)|'''Mon''']], de los [[monoide]]s y sus monoide-morfismos. Usadas en [[:en:Topological quantum field theory|TQFT]], [[álgebras de Frobenius]], [[cobordismo]]. |
|||
*La categoría '''Grp''' que consiste en todos los [[Teoría de grupos|grupos]] junto con sus [[homomorfismo|homomorfismos de grupos]]. |
|||
*La categoría '''Vect'''<sub>''K''</sub> de todos los [[espacio vectorial|espacios vectoriales]] sobre el [[cuerpo]] ''K'' junto con sus ''K''-[[Aplicación lineal|aplicaciones lineales]]. |
|||
*La categoría '''Mod'''<sub>''R''</sub> de todos los [[módulo (matemática)|módulos]] por la derecha sobre el [[anillo (matemática)|anillo]] ''R'' con unidad, junto con sus homomorfismos de módulos. Análogamente, la categoría de los módulos por la izquierda. |
|||
*La categoría [[Categoría de espacios métricos|'''Met''']] de todos los [[espacio métrico|espacios métricos]] junto a las [[Función corta|funciones cortas]]. |
|||
*La categoría [[Categoría de espacios uniformes|'''Uni''']] de todos los [[espacio uniforme|espacios uniformes]] junto a los [[unimorfismo]]s. |
|||
*La categoría [[Categoría de espacios topológicos|'''Top''']] de todos los [[espacio topológico|espacios topológicos]] junto a las [[Continuidad (matemáticas)|funciones continuas]]. |
|||
**La categoría [[Categoría de conjuntos preordenados|'''Ord''']] de todos los conjuntos preordenados junto a las [[Función|funciones]] crecientes. |
|||
***La categoría [[Categoría de conjuntos|'''Set''']] de todos los [[Conjunto|conjuntos]] junto a las [[Función|funciones]] entre los conjuntos. |
|||
*Un [[conjunto parcialmente ordenado]] (''P'', ≤) es una categoría pequeña, cuyos objetos son los miembros de ''P'', y los morfismos son las flechas desde ''x'' a ''y'' cuando ocurre que ''x'' ≤ ''y''. |
|||
*Una categoría [[monoide|monoidal]] es una categoría con una ''operación asociativa'' y un ''único elemento neutral'' con ésta operación. Los ejemplos prototípicos son la '''categoría de conjuntos''' con la operación: ''unión disjunta'' y el conjunto vacío como elemento neutro, y la '''categoría de espacios vectoriales''' sobre un cuerpo con el producto tensorial de espacios vectoriales y el mismo cuerpo como el único elemento neutral. |
|||
*Un [[Teoría de grafos|grafo]] se puede considerar como una categoría pequeña: los objetos serían los [[Vértice (Geometría)|vértices]] del grafo y los morfismos los caminos en el grafo. La composición de morfismos es la concatenación de caminos. |
|||
*Si ''I'' es un [[conjunto]], la categoría: ''categoría discreta sobre I'' es la categoría pequeña que tiene como objetos a los elementos de ''I'' y como morfismos únicamente a los morfismos identidad (que hay en toda categoría, como recordaréis). |
|||
*Cualquier categoría ''C'' puede ser considerada una nueva categoría mirándola de cierta diferente manera: los objetos serían los mismos que los de la original pero las flechas son las de la original pero con las flechas "al revés", esto es, cambiando la dirección. Se le llama la categoría ''dual'' o ''categoría opuesta'' y se denota por ''C''<sup>op</sup>. |
|||
*Si ''C'' y ''D'' son categorías, se puede formar cierto producto, el ''producto de categorías'' ''C'' x ''D'': los objetos son los pares que consisten en un objeto de cada una, uno de ''C'' y otro de ''D'', y los morfismos serían también los pares, consistiendo en un morfismo de ''C'' y otro de ''D''. Tales pares pueden ser compuestos componente a componente. |
|||
'''Arriba -la lista- no es exhaustiva y hay categorías que son subcategorías de otra.''' |
|||
== Tipos de morfismos == |
|||
Un morfismo ''f'' : ''A'' → ''B'' se le llama |
|||
* ''[[monomorfismo]]'' si ''fg<sub>1</sub>'' = ''fg<sub>2</sub>'' implica ''g<sub>1</sub>'' = ''g<sub>2</sub>'' para todos los morfismos ''g<sub>1</sub>'', ''g<sub>2</sub>'' : ''X'' → ''A''. |
|||
* ''[[epimorfismo]]'' si ''g<sub>1</sub>f'' = ''g<sub>2</sub>f'' implica ''g<sub>1</sub>'' = ''g<sub>2</sub>'' para todos los morfismos ''g<sub>1</sub>'', ''g<sub>2</sub>'' : ''B'' → ''X''. |
|||
* ''[[isomorfismo]]'' si existe un morfismo ''g'' : ''B'' → ''A'' con ''fg'' = '''id'''<sub>''B''</sub> y ''gf'' = '''id'''<sub>''A''</sub>. |
|||
* ''[[endomorfismo]]'' si ''A'' = ''B''. |
|||
* ''[[automorfismo]]'' si ''f'' es un isomorfismo y ''A'' = ''B''. |
|||
== Objetos especiales en una categoría == |
|||
Un objeto ''A'' de la categoría ''C'' es llamado |
|||
* [[Objeto inicial|inicial]], si para todo objeto ''B'' de la categoría existe un y sólo un morfismo hacia él ''A'' → ''B''. Por ejemplo el [[Conjunto vacío]] es un objeto inicial en la categoría de conjuntos. |
|||
* [[Objeto terminal|terminal]], o final, si para cada objeto ''B'' existe un y sólo un morfismo ''B'' → ''A''. Por ejemplo, cada [[singletón (matemáticas)|singletón]] (conjunto con un sólo elemento) es un objeto terminal en la categoría de conjuntos. |
|||
* [[Objeto cero|cero]], si es inicial y terminal a la vez. |
|||
== Funtores == |
|||
Los funtores son aplicaciones entre categorías que preservan la estructura. |
|||
=== Definición === |
|||
Un ''funtor'' (covariante) ''F'' de la categoría ''C'' a la categoría ''D'' |
|||
* asocia a cada objeto ''X'' en ''C'' un objeto ''F''(''X'') en ''D''; |
|||
* asocia a cada morfismo ''f'' : ''X'' → ''Y'' un morfismo ''F''(''f'') : ''F''(''X'') → ''F''(''Y'') |
|||
cumpliendo el siguiente par de propiedades |
|||
* ''F''('''id'''<sub>''X''</sub>) = '''id'''<sub>''F''(''X'')</sub> para todo objeto ''X'' en ''C''. |
|||
* ''F''(''g'' o ''f'') = ''F''(''g'') o ''F''(''f'') para todos los morfismos ''f'' : ''X'' → ''Y'' y ''g'' : ''Y'' → ''Z''. |
|||
Un ''funtor contravariante'' ''F'' de ''C'' a ''D'' es un funtor que "da la vuelta a los morfismos'' (esto es, si ''f'' : ''X'' → ''Y'' es un morfismo en ''C'', entonces ''F''(''f'') : ''F''(''Y'') → ''F''(''X'')); la manera más rápida de definir un funtor contravariante es dar un funtor covariante entre ''C''<sup>op</sup> y ''D''. |
|||
Una consecuencia importante de los axiomas para funtores es esta: si ''f'' es un isomorfismo en ''C'', entonces ''F''(''f'') también lo es en ''D''. |
|||
=== Ejemplos === |
|||
'''Espacio vectorial dual:''' un ejemplo de un funtor contravariante desde la categoría de todos los [[Espacio vectorial|espacios vectoriales]] [[Número real|reales]] a la categoría de todos los espacios vectoriales reales está dado por la asignación a cada objeto (cada espacio vectorial real) un objeto llamado [[espacio dual]] y a cada morfismo (esto es, a cada [[aplicación lineal]]), su dual o traspuesta. |
|||
'''Álgebra de las funciones continuas:''' un funtor contravariante desde la categoría de los [[Topología|espacios topológicos]] (cuyos morfismos son las aplicaciones continuas) a la categoría de las [[Álgebra asociativa|álgebras asociativas]] reales, es dado asignando a cada espacio topológico''X'' el álgebra C(''X'') de todas las funciones reales continuas sobre tal espacio. Cada aplicación continua ''f'' : ''X'' → ''Y'' (morfismo en la categoría de espacios topológicos) induce un homomorfismo de álgebras C(''f'') : C(''Y'') → C(''X'') mediante la regla C(''f'')(φ) = φ o ''f'' para todo φ en C(''Y''). |
|||
'''Homomorfismo de grupos:''' a cada par ''A'', ''B'' de [[Teoría de grupos|grupos abelianos]] se puede asignar el grupo abeliano Hom(''A'',''B'') que consiste en todos [[Homomorfismo|homomorfismos de grupos]] desde ''A'' a ''B''. Esto es un funtor que es contravariante en el primer argumento y covariante en el segundo, esto es, es un funtor '''Ab'''<sup>op</sup> x '''Ab''' → '''Ab''' (donde '''Ab''' denota la categoría de los grupos abelianos con los homomorfismos de grupos). Si ''f'' : ''A''<sub>1</sub> → ''A''<sub>2</sub> and ''g'' : ''B''<sub>1</sub> → ''B''<sub>2</sub> son morfismos en '''Ab''', entonces se tiene este homomorfismo Hom(''f'',''g'') : Hom(''A''<sub>2</sub>,''B''<sub>1</sub>) → Hom(''A''<sub>1</sub>,''B''<sub>2</sub>) dado por φ |→ ''g'' o φ o ''f''. |
|||
'''Funtores 'Olvido', o 'Forgetful':''' el funtor ''F'' : '''Ring''' → '''Ab''' que aplica un [[Anillo (álgebra)|anillo]] hacia su grupo subyacente [[abeliano]] es un funtor que olvida ("forgetful"), que nos crea una imagen de algo más "rico" en un objeto más pobre, con menos estructura. Los morfismos en la categoría de '''Anillos''' (homomorfismos de anillos) se convierten en morfismos en '''Ab''' (la categoría de grupos abelianos y sus homomorfismos). |
|||
'''Productos tensoriales:''' Si ''C'' denota la categoría de los espacios vectoriales sobre un cuerpo fijado, con las [[Aplicación lineal|aplicaciones lineales]] como morfismos, entonces el [[producto tensorial]] ''V'' [símbolo] ''W'' define un funtor ''C'' × ''C'' → ''C'' que es covariante en ambos argumentos. |
|||
'''Álgebras de Lie:''' A cada [[grupo de Lie]] real o complejo se le asigna su real (o compleja) [[Álgebra de Lie]], con lo que se define un funtor. |
|||
'''Grupo fundamental:''' Considera la categoría de los [[Espacio topológico|espacios topológicos]] con "puntos base", con "puntos distinguidos". Los objetos son los pares (''X'',''x''), donde ''X'' es un espacio topológico y ''x'' es un elemento de ''X''. Un morfismo desde (''X'',''x'') hacia (''Y'',''y'') viene dado por una [[aplicación continua]] ''f'' : ''X'' → ''Y'' tal que ''f''(''x'') = ''y''. |
|||
Para cada espacio topológico con punto base (''X'',''x''), definiremos un [[grupo fundamental]]. El cual va a ser un funtor desde la categoría de los espacios topológicos con puntos base hacia la categoría de los grupos. |
|||
Sea ''f'' una función continua desde el [[intervalo unidad]] [0,1] hacia ''X'' tal que ''f''(0) = ''f''(1) = ''x''. (Esto es equivalente a que, ''f'' sea una aplicación continua desde el [[círculo]] unidad en el plano complejo tal que ''f''(1) = ''x''.) Llamamos a tal función un lazo en ''X''. Si ''f'' y ''g'' son lazos en ''X'', podemos pegarlos uno a continuación del otro definiendo ''h''(''t'') = ''f''(2''t'') cuando ''t'' recorra [0,0.5] y ''h''(''t'') = ''g''(2(''t'' - 0.5)) cuando ''t'' recorra [0.5,1]. Es fácil comprobar que este ''h'' también es un lazo. Si existe una aplicación continua ''F''(''x'',''t'') desde [0,1] × [0,1] a ''X'' tal que ''f''(''t'') = ''F''(0,''t'') es un lazo y ''g''(''t'') = ''F''(1,''t'') es también un lazo entonces se dice que ''f'' y ''g'' son equivalentes. Se puede probar que esto define una [[relación de equivalencia]]. Nuestra regla de composición asegura que todo vaya bien. Ahora, además, podemos ver que se tiene un elemento neutro ''e''(''t'') = ''x'' (una aplicación constante) y que cada lazo tiene un lazo inverso. De hecho, si ''f''(''t'') es un lazo entonces ''f''(1 - ''t'') es su inverso. El conjunto de clases de equivalencia de lazos forma entonces un grupo (el [[grupo fundamental]] de ''X''). Se puede comprobar que la aplicación desde la categoría de espacios topológicos con punto base a la categoría de grupos es funtorial: un (homo/iso)morfismo topológico se hará corresponder naturalmente a un (homo/iso)morfismo de grupos. |
|||
'''[[Teoría de haces]]: prehaces.''' Si ''X'' es un [[Topología|espacio topológico]], entonces los conjuntos abiertos en ''X'' pueden ser considerados como los objetos de una categoría ''C<sub>''X''</sub>''; existiendo un morfismo de ''U'' a ''V'' si y sólo si ''U'' es un [[subconjunto]] de ''V''. En sí misma, esta categoría no es muy excitante, pero los funtores desde ''C<sub>''X''</sub>''<sup>op</sup> hacia otras categorías, llamados ''pre-haces sobre X'', son interesantes. Por ejemplo, asignando a cada conjunto abierto ''U'' el [[álgebra asociativa]] de las funciones reales sobre ''U'', se obtiene un pre-haz de álgebras sobre ''X''. |
|||
Este ejemplo de motivación se generaliza mediante la consideración de pre-haces sobre categorías arbitrarias: un pre-haz sobre ''C'' es un funtor definido sobre ''C''<sup>op</sup>. El [[Lema de Yoneda]] da cuenta de que a menudo una categoría ''C'' puede extenderse mediante la consideración de la categoría de pre-haces sobre ''C''. |
|||
'''La Categoría de las categorías pequeñas:''' La categoría '''Cat''' posee como objetos a todas las categorías pequeñas, y como morfismos a los funtores entre ellas. |
|||
== Construcciones universales == |
|||
Los funtores son a menudo definidos por medio de [[propiedad universal|propiedades universales]]; como ejemplos tenemos los productos tensoriales de arriba, la [[suma directa]] y el [[producto directo]] de grupos o de espacios vectoriales, la construcción de los grupos libres módulos, y límites [[límite directo|directos]] e [[límite inverso|inversos]]. Los conceptos de [[límite (Teoría de categorías)|límite y colímite]] generalizan múltiples conceptos. |
|||
Las construcciones universales a menudo dan lugar a pares de [[funtores adjuntos]]. |
|||
== Otros conceptos y resultados == |
|||
Las definiciones de categorías y funtores nos proveen sólo de la base inicial del álgebra categorial. Los tópicos listados abajo son muy importantes. Aunque hay fuertes interrelaciones entre todos ellos, el orden en que los damos puede ser considerado una guía para posteriores lecturas. |
|||
* [[transformación natural]]: Mientras los funtores dan un camino para pasar, imprimir una categoría en otra, las transformaciones naturales nos proveen de una relación similar entre funtores. |
|||
* El [[Lema de Yoneda]] es uno de los resultados más famosos de la teoría de categorías. |
|||
* [[límite (Teoría de categorías)|Límites y colímites]]: Para introducir ciertas construcciones como los productos (de conjuntos, de topologías, de órdenes parciales, ...), en la teoría, los límites y los colímites son de ayuda. |
|||
* [[funtores adjuntos]]: Un funtor puede ser el adjunto por la izquierda (o por la derecha) de otro funtor que vaya en la dirección opuesta. Sin embargo, cuando los comparamos con las relaciones clásicas de las aplicaciones que preservan las estructuras (inversas...), el concepto de adjunción de funtores aparenta ser bastante abstracto y general. Es de gran utilidad aún y tiene relación con muchos otros conceptos importantes, como ocurre en la construcción de límites. |
|||
* [[equivalencia de categorías]]: Para obtener un criterio adecuado para discernir si dos categorías pueden o no ser consideradas similares, es necesario encontrar una noción más general que el concepto clásico de [[isomorfismo]]. Las equivalencias de categorías están muy relacionadas con related con '''dualidad de categorías'''. |
|||
* [[diagrama conmutativo|diagramas conmutativos]]: Ya que la teoría de categorías trata usualmente con objetos y flechas es conveniente expresar las identidades mediante diagramas. |
|||
== Bibliografía == |
|||
Los dos textos de Lawvere son las introducciones más sencillas que existen. |
|||
El de Mac Lane es uno "clásico" en esta materia, y el Borceaux es una pequeña enciclopedia. |
|||
* [[William Lawvere]] & [[Steve Schanuel]], ''Matemáticas Conceptuales: Una primera introducción a categorías'', Siglo XXI, 2002 (traducción de Marmolejo Rivas, Francisco a partir de ''Conceptual Mathematics: A First Introduction to Categories'', Cambridge University Press, Cambridge, 1997). |
|||
* [[William Lawvere]] & [[Steve Schanuel]], ''Sets for mathematics'', Cambridge University Press, 2003. |
|||
* [[Saunders Mac Lane]] (1998): ''Categories for the Working Mathematician'', Graduate Texts in Mathematics 5, Springer; ISBN 0-387-98403-8 |
|||
* [[Francis Borceux]]. ''Handbook of Categorical Algebra'', volumes 50-52 of ''Encyclopedia of Mathematics and its Applications''. Cambridge University Press, 1994. |
|||
== Enlaces externos == |
|||
* Un proyecto en castellano que pretende comenzar la divulgación en castellano es el de: |
|||
http://arrows.ourproject.org/ |
|||
* "Category Theory" artículo en inglés de Jean-Pierre Marquis en la ''Stanford Encyclopedia of Philosophy'' [http://plato.stanford.edu/entries/category-theory/]. |
|||
*{{planetmath reference|oid=5622|title=Category Theory.}} |
|||
[[Categoría:Teoría de categorías]] |
|||
[[Categoría:Teorías matemáticas|Categorias]] |
|||
[[ar:نظرية التصنيف]] |
|||
[[bg:Теория на категориите]] |
|||
[[ca:Teoria de categories]] |
|||
[[cs:Teorie kategorií]] |
|||
[[da:Kategoriteori]] |
|||
[[de:Kategorientheorie]] |
|||
[[el:Θεωρία κατηγοριών]] |
|||
[[en:Category theory]] |
|||
[[eo:Teorio de kategorioj]] |
|||
[[fa:نظریه ردهها]] |
|||
[[fr:Théorie des catégories]] |
|||
[[he:תורת הקטגוריות]] |
|||
[[it:Teoria delle categorie]] |
|||
[[ja:圏論]] |
|||
[[ka:კატეგორიათა თეორია]] |
|||
[[ko:범주론]] |
|||
[[nl:Categorietheorie (wiskunde)]] |
|||
[[pl:Teoria kategorii]] |
|||
[[pt:Teoria das categorias]] |
|||
[[ru:Теория категорий]] |
|||
[[sv:Kategoriteori]] |
|||
[[tr:Kategori teorisi]] |
|||
[[zh:范畴论]] |
|||
Revisión del 03:02 6 jun 2009
La teoría de categorías es una teoría matemática que trata de forma abstracta con las estructuras matemáticas y sus relaciones.
La teoría de las categorías fue introducida en Topología algebraica, por Samuel Eilenberg y Saunders MacLane, en un importante paso para la transición desde homología (un concepto geométrico intuitivo) a Teoría de la homología (una materia axiomática). Se ha reclamado que existieron ideas parecidas en la escuela polaca de los años 1930 (ver Stanislaw Ulam).
Los desarrollos subsiguientes de la teoría fueron impulsados por las necesidades computacionales del Álgebra homológica y más tarde por las necesidad de axiomáticas en Geometría algebraica, que era el campo más reacio a pasar por el aro de los fundamentos unificadores à la Russell-Whitehead. La teoría general -cierta actualización del Álgebra universal con muchas características nuevas que daban pie a una cierta flexibilidad en semántica y lógicas de orden superior- vino más tarde.
Las aplicaciones de esta teoría en fundamentos están provocando cierta controversia [cita requerida].
Estas aplicaciones de categorías en el campo de los fundamentos están siendo trabajadas en bastante detalle y no solamente en matemáticas. Existen matemáticos como William Lawvere que trabajan en la física, existen físicos trabajando en n-categorías, John Baez, e incluso hay filósofos como Alain Badiou en Francia o Corfield en Inglaterra que se han visto obligados a poner sus "indagaciones" bajo las condiciones de la matemática contemporánea. Una idea sobre lo que está pasando se trasluce en algunos escasos libros de texto clásicos en el mundo anglosajón: el "abstract algebra" de Birkhoff- Mac Lane que después pasa a ser el mismo "abstract algebra" pero de Mac Lane-Birkhoff.
La Lógica Categórica es ahora un campo bien definido basado en la teoría de tipos para la Lógica intuicionista, con aplicaciones a la teoría de la programación funcional y la teoría de dominios, todas enmarcadas en una categoría cartesianamente cerrada como descripciones no sintácticas del cálculo lambda. El uso del lenguaje de la teoría de las categorías le permite a uno aclarar qué tienen exactamente en común todas estas áreas.
Categorías
Con el concepto de categoría se pretende capturar -poniendo el énfasis en el concepto de relación, de flecha, más que de elemento y pertenencia- la esencia de una clase de objetos matemáticos, que se relacionan mediante las flechas, los morfismos en la categoría en cuestión. Por ejemplo, la clase de los grupos. En vez de estudiar los objetos individuales (cada grupo) como se vino haciendo, se enfatizan dichos morfismos entre ellos, que no son otra cosa que las aplicaciones que "conservan su estructura". En el ejemplo de los grupos, dichos morfismos son los homomorfismos de grupos. Entonces, una vez que tenemos nuestro "universo categorial" definido -esto es, una categoría- es posible relacionarla con otras categorías mediante funtores, que son cierta generalización del concepto de función para categorías: un funtor asocia a cada objeto de una categoría un objeto de la otra, y a cada flecha de la primera una flecha de la segunda. De cierto modo nos "plasma", nos lleva una imagen de la categoría hacia la otra categoría y con ciertos grados de "afinamiento". Ciertas "construcciones naturales", como el grupo fundamental de un espacio topológico, pueden ser expresadas como funtores. Además, dichos funtores están muy a menudo naturalmente relacionados y esto lleva al concepto de transformación natural.
Históricamente, fue precisamente la motivación de clarificar ciertas transformaciones naturales en Topología algebraica lo que sirvió para definir los funtores y las categorías. Y, enseguida, la teoría fue aplicada en Álgebra homológica y en Geometría algebraica; ahora se usa en bastantes ramas de la matemática, la física y la filosofía.
Categorías especiales, como los topos, están sirviendo también como alternativa "generalizadora" y conceptualmente más rica de la teoría de conjuntos como fundamento de las matemáticas [cita requerida].
Definición
Una categoría consiste en:
- una clase de cosas llamadas objetos. (Una clase es "más" que un conjunto, una clase propia no puede ser elemento de ninguna clase).
- y para cada par de objetos A y B un conjunto Mor(A,B) de cosas llamadas morfismos de A a B. Si f está en dicho conjunto Mor(A,B), escribiremos f : A → B.
- para cada tres objetos A, B y C hay una operación binaria Mor(A,B) × Mor(B,C) → Mor(A,C) llamada composición de morfismos. La composición de f : A → B y g : B → C se escribe así: g o f o bien gf. (Y algunos autores: fg);
tal que todo ello sigue los siguientes axiomas:
- (asociatividad) si f : A → B, g : B → C y h : C → D entonces h o (g o f) = (h o g) o f, y
- (identidad) para cada objeto X existe un morfismo idX : X → X llamado morfismo identidad en X, tal que para todo morfismo f : A → B se tiene idB o f = f = f o idA
De estos axiomas se puede probar que se tiene sólo un morfismo identidad para cada objeto.
Si las clases de los objetos y los morfismos son solamente conjuntos, pero no clases, se dice que la categoría es "pequeña" (small category). Existen importantes categorías que no lo son.
Ejemplos
Cada categoría es presentada en términos de sus objetos y morfismos.
- La categoría Mag de todos los magmas junto con sus homomorfismos.
- La categoría Med de todos los magmas mediales junto con sus homomorfismos.
- La cat Mon, de los monoides y sus monoide-morfismos. Usadas en TQFT, álgebras de Frobenius, cobordismo.
- La categoría Grp que consiste en todos los grupos junto con sus homomorfismos de grupos.
- La categoría VectK de todos los espacios vectoriales sobre el cuerpo K junto con sus K-aplicaciones lineales.
- La categoría ModR de todos los módulos por la derecha sobre el anillo R con unidad, junto con sus homomorfismos de módulos. Análogamente, la categoría de los módulos por la izquierda.
- La categoría Met de todos los espacios métricos junto a las funciones cortas.
- La categoría Uni de todos los espacios uniformes junto a los unimorfismos.
- La categoría Top de todos los espacios topológicos junto a las funciones continuas.
- Un conjunto parcialmente ordenado (P, ≤) es una categoría pequeña, cuyos objetos son los miembros de P, y los morfismos son las flechas desde x a y cuando ocurre que x ≤ y.
- Una categoría monoidal es una categoría con una operación asociativa y un único elemento neutral con ésta operación. Los ejemplos prototípicos son la categoría de conjuntos con la operación: unión disjunta y el conjunto vacío como elemento neutro, y la categoría de espacios vectoriales sobre un cuerpo con el producto tensorial de espacios vectoriales y el mismo cuerpo como el único elemento neutral.
- Un grafo se puede considerar como una categoría pequeña: los objetos serían los vértices del grafo y los morfismos los caminos en el grafo. La composición de morfismos es la concatenación de caminos.
- Si I es un conjunto, la categoría: categoría discreta sobre I es la categoría pequeña que tiene como objetos a los elementos de I y como morfismos únicamente a los morfismos identidad (que hay en toda categoría, como recordaréis).
- Cualquier categoría C puede ser considerada una nueva categoría mirándola de cierta diferente manera: los objetos serían los mismos que los de la original pero las flechas son las de la original pero con las flechas "al revés", esto es, cambiando la dirección. Se le llama la categoría dual o categoría opuesta y se denota por Cop.
- Si C y D son categorías, se puede formar cierto producto, el producto de categorías C x D: los objetos son los pares que consisten en un objeto de cada una, uno de C y otro de D, y los morfismos serían también los pares, consistiendo en un morfismo de C y otro de D. Tales pares pueden ser compuestos componente a componente.
Arriba -la lista- no es exhaustiva y hay categorías que son subcategorías de otra.
Tipos de morfismos
Un morfismo f : A → B se le llama
- monomorfismo si fg1 = fg2 implica g1 = g2 para todos los morfismos g1, g2 : X → A.
- epimorfismo si g1f = g2f implica g1 = g2 para todos los morfismos g1, g2 : B → X.
- isomorfismo si existe un morfismo g : B → A con fg = idB y gf = idA.
- endomorfismo si A = B.
- automorfismo si f es un isomorfismo y A = B.
Objetos especiales en una categoría
Un objeto A de la categoría C es llamado
- inicial, si para todo objeto B de la categoría existe un y sólo un morfismo hacia él A → B. Por ejemplo el Conjunto vacío es un objeto inicial en la categoría de conjuntos.
- terminal, o final, si para cada objeto B existe un y sólo un morfismo B → A. Por ejemplo, cada singletón (conjunto con un sólo elemento) es un objeto terminal en la categoría de conjuntos.
- cero, si es inicial y terminal a la vez.
Funtores
Los funtores son aplicaciones entre categorías que preservan la estructura.
Definición
Un funtor (covariante) F de la categoría C a la categoría D
- asocia a cada objeto X en C un objeto F(X) en D;
- asocia a cada morfismo f : X → Y un morfismo F(f) : F(X) → F(Y)
cumpliendo el siguiente par de propiedades
- F(idX) = idF(X) para todo objeto X en C.
- F(g o f) = F(g) o F(f) para todos los morfismos f : X → Y y g : Y → Z.
Un funtor contravariante F de C a D es un funtor que "da la vuelta a los morfismos (esto es, si f : X → Y es un morfismo en C, entonces F(f) : F(Y) → F(X)); la manera más rápida de definir un funtor contravariante es dar un funtor covariante entre Cop y D.
Una consecuencia importante de los axiomas para funtores es esta: si f es un isomorfismo en C, entonces F(f) también lo es en D.
Ejemplos
Espacio vectorial dual: un ejemplo de un funtor contravariante desde la categoría de todos los espacios vectoriales reales a la categoría de todos los espacios vectoriales reales está dado por la asignación a cada objeto (cada espacio vectorial real) un objeto llamado espacio dual y a cada morfismo (esto es, a cada aplicación lineal), su dual o traspuesta.
Álgebra de las funciones continuas: un funtor contravariante desde la categoría de los espacios topológicos (cuyos morfismos son las aplicaciones continuas) a la categoría de las álgebras asociativas reales, es dado asignando a cada espacio topológicoX el álgebra C(X) de todas las funciones reales continuas sobre tal espacio. Cada aplicación continua f : X → Y (morfismo en la categoría de espacios topológicos) induce un homomorfismo de álgebras C(f) : C(Y) → C(X) mediante la regla C(f)(φ) = φ o f para todo φ en C(Y).
Homomorfismo de grupos: a cada par A, B de grupos abelianos se puede asignar el grupo abeliano Hom(A,B) que consiste en todos homomorfismos de grupos desde A a B. Esto es un funtor que es contravariante en el primer argumento y covariante en el segundo, esto es, es un funtor Abop x Ab → Ab (donde Ab denota la categoría de los grupos abelianos con los homomorfismos de grupos). Si f : A1 → A2 and g : B1 → B2 son morfismos en Ab, entonces se tiene este homomorfismo Hom(f,g) : Hom(A2,B1) → Hom(A1,B2) dado por φ |→ g o φ o f.
Funtores 'Olvido', o 'Forgetful': el funtor F : Ring → Ab que aplica un anillo hacia su grupo subyacente abeliano es un funtor que olvida ("forgetful"), que nos crea una imagen de algo más "rico" en un objeto más pobre, con menos estructura. Los morfismos en la categoría de Anillos (homomorfismos de anillos) se convierten en morfismos en Ab (la categoría de grupos abelianos y sus homomorfismos).
Productos tensoriales: Si C denota la categoría de los espacios vectoriales sobre un cuerpo fijado, con las aplicaciones lineales como morfismos, entonces el producto tensorial V [símbolo] W define un funtor C × C → C que es covariante en ambos argumentos.
Álgebras de Lie: A cada grupo de Lie real o complejo se le asigna su real (o compleja) Álgebra de Lie, con lo que se define un funtor.
Grupo fundamental: Considera la categoría de los espacios topológicos con "puntos base", con "puntos distinguidos". Los objetos son los pares (X,x), donde X es un espacio topológico y x es un elemento de X. Un morfismo desde (X,x) hacia (Y,y) viene dado por una aplicación continua f : X → Y tal que f(x) = y.
Para cada espacio topológico con punto base (X,x), definiremos un grupo fundamental. El cual va a ser un funtor desde la categoría de los espacios topológicos con puntos base hacia la categoría de los grupos.
Sea f una función continua desde el intervalo unidad [0,1] hacia X tal que f(0) = f(1) = x. (Esto es equivalente a que, f sea una aplicación continua desde el círculo unidad en el plano complejo tal que f(1) = x.) Llamamos a tal función un lazo en X. Si f y g son lazos en X, podemos pegarlos uno a continuación del otro definiendo h(t) = f(2t) cuando t recorra [0,0.5] y h(t) = g(2(t - 0.5)) cuando t recorra [0.5,1]. Es fácil comprobar que este h también es un lazo. Si existe una aplicación continua F(x,t) desde [0,1] × [0,1] a X tal que f(t) = F(0,t) es un lazo y g(t) = F(1,t) es también un lazo entonces se dice que f y g son equivalentes. Se puede probar que esto define una relación de equivalencia. Nuestra regla de composición asegura que todo vaya bien. Ahora, además, podemos ver que se tiene un elemento neutro e(t) = x (una aplicación constante) y que cada lazo tiene un lazo inverso. De hecho, si f(t) es un lazo entonces f(1 - t) es su inverso. El conjunto de clases de equivalencia de lazos forma entonces un grupo (el grupo fundamental de X). Se puede comprobar que la aplicación desde la categoría de espacios topológicos con punto base a la categoría de grupos es funtorial: un (homo/iso)morfismo topológico se hará corresponder naturalmente a un (homo/iso)morfismo de grupos.
Teoría de haces: prehaces. Si X es un espacio topológico, entonces los conjuntos abiertos en X pueden ser considerados como los objetos de una categoría CX; existiendo un morfismo de U a V si y sólo si U es un subconjunto de V. En sí misma, esta categoría no es muy excitante, pero los funtores desde CXop hacia otras categorías, llamados pre-haces sobre X, son interesantes. Por ejemplo, asignando a cada conjunto abierto U el álgebra asociativa de las funciones reales sobre U, se obtiene un pre-haz de álgebras sobre X.
Este ejemplo de motivación se generaliza mediante la consideración de pre-haces sobre categorías arbitrarias: un pre-haz sobre C es un funtor definido sobre Cop. El Lema de Yoneda da cuenta de que a menudo una categoría C puede extenderse mediante la consideración de la categoría de pre-haces sobre C.
La Categoría de las categorías pequeñas: La categoría Cat posee como objetos a todas las categorías pequeñas, y como morfismos a los funtores entre ellas.
Construcciones universales
Los funtores son a menudo definidos por medio de propiedades universales; como ejemplos tenemos los productos tensoriales de arriba, la suma directa y el producto directo de grupos o de espacios vectoriales, la construcción de los grupos libres módulos, y límites directos e inversos. Los conceptos de límite y colímite generalizan múltiples conceptos. Las construcciones universales a menudo dan lugar a pares de funtores adjuntos.
Otros conceptos y resultados
Las definiciones de categorías y funtores nos proveen sólo de la base inicial del álgebra categorial. Los tópicos listados abajo son muy importantes. Aunque hay fuertes interrelaciones entre todos ellos, el orden en que los damos puede ser considerado una guía para posteriores lecturas.
- transformación natural: Mientras los funtores dan un camino para pasar, imprimir una categoría en otra, las transformaciones naturales nos proveen de una relación similar entre funtores.
- El Lema de Yoneda es uno de los resultados más famosos de la teoría de categorías.
- Límites y colímites: Para introducir ciertas construcciones como los productos (de conjuntos, de topologías, de órdenes parciales, ...), en la teoría, los límites y los colímites son de ayuda.
- funtores adjuntos: Un funtor puede ser el adjunto por la izquierda (o por la derecha) de otro funtor que vaya en la dirección opuesta. Sin embargo, cuando los comparamos con las relaciones clásicas de las aplicaciones que preservan las estructuras (inversas...), el concepto de adjunción de funtores aparenta ser bastante abstracto y general. Es de gran utilidad aún y tiene relación con muchos otros conceptos importantes, como ocurre en la construcción de límites.
- equivalencia de categorías: Para obtener un criterio adecuado para discernir si dos categorías pueden o no ser consideradas similares, es necesario encontrar una noción más general que el concepto clásico de isomorfismo. Las equivalencias de categorías están muy relacionadas con related con dualidad de categorías.
- diagramas conmutativos: Ya que la teoría de categorías trata usualmente con objetos y flechas es conveniente expresar las identidades mediante diagramas.
Bibliografía
Los dos textos de Lawvere son las introducciones más sencillas que existen. El de Mac Lane es uno "clásico" en esta materia, y el Borceaux es una pequeña enciclopedia.
- William Lawvere & Steve Schanuel, Matemáticas Conceptuales: Una primera introducción a categorías, Siglo XXI, 2002 (traducción de Marmolejo Rivas, Francisco a partir de Conceptual Mathematics: A First Introduction to Categories, Cambridge University Press, Cambridge, 1997).
- William Lawvere & Steve Schanuel, Sets for mathematics, Cambridge University Press, 2003.
- Saunders Mac Lane (1998): Categories for the Working Mathematician, Graduate Texts in Mathematics 5, Springer; ISBN 0-387-98403-8
- Francis Borceux. Handbook of Categorical Algebra, volumes 50-52 of Encyclopedia of Mathematics and its Applications. Cambridge University Press, 1994.
Enlaces externos
- Un proyecto en castellano que pretende comenzar la divulgación en castellano es el de:
- "Category Theory" artículo en inglés de Jean-Pierre Marquis en la Stanford Encyclopedia of Philosophy [1].
- Category Theory. en PlanetMath.
