Anillo cíclico

Definición

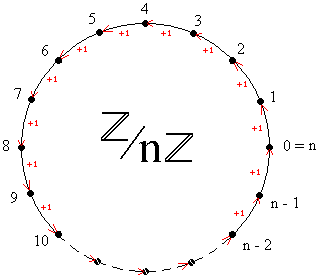
Los anillos son estructuras matemáticas sencillas que generalizan las propiedades de la adición y la multiplicación (asociatividad, conmutatividad, distributividad, elemento neutro, opuesto...) del conjunto de los enteros relativos Z en particular.

Los anillos cíclicos se caracterizan por ser generados por un solo elemento (se dicen monogéneos) y por ser finitos. Más precisamente, para todo número natural n ≥ 2 existe un único anillo cíclico (mediante isomorfismos) de orden (tamaño) n, se lo nota Z/nZ(como cociente del anillo Z por el ideal nZ), Z/(n) (nZ, ideal generado por n se escribe también (n) ) o Z_n, y se puede representar como en la figura.
Fueron los primeros anillos descubiertos después de Z y la apelación "anillo" proviene evidentemente de la figura anterior.

Cálculo elemental

En el anillo Z_n, la suma y el producto son los usuales en Z con una regla adicional: se decide que los números n y 0 son iguales: se escribe n ≡ 0 o n ≡ 0 (mod n) para ser más preciso, cuando uno se sitúa en Z, y ${\overline {n}}={\overline {o}}$ cuando se trabaja en Z_n (ā es una manera arbitraria de designar la clase de equivalencia de a en Z_n - no se empleará aquí esta notación).
Aplicando varias veces lo anterior se muestra que es lícito añadir o sustraer cuantas veces se quiere "n" a un término sin cambiar su valor en Z_n :

a ≡ a + k·n (mod n), con k ∈ Z.

Se dice que a y a + k·n son iguales módulo n o congruentes módulo n y se llama cálculo modular o congruencias esta clase de igualdades.

Por ejemplo en Z₁₀: 1968 ≡ 8, porque 1968 = 196×10 + 8.

En este ejemplo, 8 es el resto de la división euclidiana de 1968 por 10, y de hecho cada división da lugar a una congruencia:

el resto y el dividendo son iguales módulo el divisor
si a = b·q + r, entonces r ≡ a (mod q)

La relación ≡ se puede ver como una congruencia en Z o como una igualdad en Z_n. Como hemos decidido no distinguir el entero a de su clase ā, una misma relación a ≡ b (mod n) tiene dos interpretaciones. Verla como una igualdad conlleva la ventaja de ser mucho más intuitivo; por ejemplo las propiedades siguientes no sorprenderán:

Sean a₁,a₂, b₁, b₂ enteros (o elementos de Z_n), y m un natural, entonces:

${\mbox{si }}\ a_{1}\equiv a_{2}\ y\ \ b_{1}\equiv b_{2}\ \ {\mbox{entonces }}\left\{{\begin{matrix}a_{1}+b_{1}\equiv a_{2}+b_{2},\\a_{1}b_{1}\equiv a_{2}b_{2},\\a_{1}^{m}\equiv a_{2}^{m}\end{matrix}}\right.$

Aplicaciones directas a la aritmética

• Los criterios de divisibilidad por 3, 9 y 11 son consecuencia directa de las relaciones anteriores.

Consideremos el más conocido, el criterio por 9. Sea un número n cuyas cifras son a_o (unidades), a₁ (decenas), a₂ (centenares)...

Es costumbre escribirlo $n={\overline {a_{p}a_{p-1}...a_{2}a_{1}a_{o}}}$ para distinguirlo del producto $n=a_{p}a_{p-1}...a_{2}a_{1}a_{o}\quad$ y vale, en escritura clásica: $n=a_{p}10^{p}+a_{p-1}10^{p-1}+...+a_{2}10^{2}+a_{1}10+a_{o}\quad$

Como $10\equiv 1\;(mod\;9)$ entonces para todo k entero positivo $10^{p}\equiv 1^{p}\equiv 1\;(mod\;9)\quad$, y sumando los términos que aparecen en n se obtiene: $n=a_{p}10^{p}+...+a_{1}10+a_{o}\equiv a_{p}+a_{p-1}+...+a_{1}+a_{0}\;(mod\;9)$

Es decir que el resto módulo 9 se obtiene sumando las cifras del número. Para verificar un cálculo, por ejemplo un producto: a = b×c, se miran los restos módulo 9, a', b' y c', y si a'≠b'×c' (mod 9) entonces el cálculo es erróneo. En caso contrario no se puede concluir.

• Las congruencias permiten también resolver problemillos esencialmente lúdicos al estilo hallar la cifra de las unidades de 2003²⁰⁰⁵.

Un ordenador común y corriente es incapaz de calcular tamaño número. Buena ocasión para subrayar la superioridad de la inteligencia humana sobre la artificial, y lucirse a la primera oportunidad...
Encontrar la cifra de las unidades se logra trabajando módulo 10, pues el resto de la división por 10 es justamente esta cifra.
Como 2003 ≡ 3 (mod 10), 2003²⁰⁰⁵ ≡ 3²⁰⁰⁵, luego nos toca mirar los 3^k (mod 10):
3⁰ ≡ 1, 3¹ ≡ 3, 3² = 9 ≡ 9, 3³ = 27 ≡ 7, 3⁴ = 81 ≡ 1.
Este último resultado permite generalizar: 3^4k ≡ 1, para todo k natural.
Luego dividimos 2005 por 4: 2005 = 4×501 + 1.
Finalmente 3²⁰⁰⁵ = 3^{4×501 + 1} = 3^4×501× 3¹ ≡ 1 × 3 = 3 (mod 10).
La cifra buscada es 3.

Elementos inversibles

La adición, sustracción y multiplicación se comportan como era de esperar en los anillos cíclicos. Pero ¿ Qué hay de la división ?
Dividir por un número es por definición multiplicar por su inverso. La cuestión es entonces averiguar cuales son los elementos inversibles del anillo. El número a es inversible en Z/(n) si y sólo si existe b tal que:

a·b ≡ 1 (mod n)     lo que se escribe:     a·b = 1 + k·n, k ∈ Z     es decir: a·b - k·n = 1.

Esto es una identidad de Bézout y tiene soluciones si y sólo si a y n son números coprimos (es decir primos entre sí: su máximo común divisor es 1 ).
Ejemplos:

• 2 y 5, al ser número primos distintos, son coprimos, entonces 2 es inversible en Z₅. Una relación de Bézout es 2×3 - 1×5 = 1 que da 2×3 ≡ 1 (mod 5), por consiguiente el inverso de 2 es 3 en Z₅. En efecto 2×3 = 6 ≡ 1 (mod 5).
• 7 y 12 son coprimos porque el número primo 7 no aparece en la descomposición en factores primos de 12 = 2²×3.

El algoritmo de Euclides permite obtener la relación de Bezout:

3×12 - 5×7 = 1    que da la congruencia:    -5×7 ≡ 1 (mod 12).

-5 es por lo tanto el inverso de 7 en Z₁₂. Pero -5 ≡ 7 (mod 12), por consiguiente 7 es su propio inverso en Z₁₂, lo que se verifica rápidamente: 7² = 49 = 4×12 + 1 ≡ 1 (mod 12).

El número de elemento inversibles de Z_n se nota φ(n), donde φ es la función fi de Euler.
Si n es primo, y sólo en este caso, todos los enteros naturales no nulos inferiores a n son coprimos con n; esto implica que serán todos inversible en Z_n, lo que convierte este anillo en un cuerpo a veces denotado F_n.

Universalidad de los anillos cíclicos

Sea A un anillo finito, cuyo neutro (para la multiplicación) denotamos e. El conjunto de los múltiplos de e, C = {0, e, 2·e, 3·e, 4·e...} por ser incluido en A es también finito. Entonces a partir de cierto valor de m, m·e ya fue listado en C, es decir que existe k < m tal que k·e = m·e. Por sustracción n·e = 0 con n = m - k.
Sea n el menor entero natural no nulo tal que n·e = 0. Luego C = {0, e, 2·e, 3·e, 4·e...(n-1)·e} es decir que C es isomorfo al anillo cíclico de orden n. Además C pertenece al centro de A, pues sus elementos conmuten con todos los de A.
El número n verifica además la propiedad de anular todos los elementos de A: para todo a ∈ A, n·a = n·e·a = 0·a = 0. Es el menor natural no nulo que tiene esta propiedad, y recibe el nombre de característica del anillo.

En resumen:

Todo anillo finito tiene en su centro un anillo cíclico.
Su orden es la característica del anillo
La estructura del anillo es definida en gran medida por su anillo cíclico

En efecto, el producto :

$C\times A\rightarrow A$
$(c,a)\rightarrow c\cdot a$

Convierte en anillo A en un módulo sobre C = Z_n. en particular, si la característica n es un primo, entonces A es un espacio vectorial sobre el cuerpo C = Z_n, y como tal es forzosamente ismorfo a Cⁿ. El producto interior le da además una estructura de álgebra.

Productos de anillos cíclicos

Teorema:

Para todo par (a, b) de enteros coprimos, Z_a·b es isomorfo al producto de anillos Z_a×Z_b.

Esta permite descomponer un anillo cíclico Z_n en otros menores, según la factorización en números primos de n.

Prueba:

Consideremos la aplicación lineal f:

Z → Z_a× Z_b

 n → (n mod a, n mod b)        ("n mod a" es la clase de n en Z_a)

El núcleo de esta aplicación es el conjunto de los n divisibles a la vez por a y por b; son por lo tanto los múltiplos de mínimo común múltiplo de a y b que es ab porque a y b son coprimos: El núcleo es Ker f = a·bZ.
Como a y b son coprimos, el teorema de los restos chinos, consecuencia de la identidad de Bézout afirma que f es sobreyectiva: Im f = Z_a×Z_b. Según la descomposición de una aplicación lineal existe un isomorfismo (luego una biyección) entre Z/Ker f e Im f es decir entre Z_a·b y Z_a× Z_b.

La biyección se obtiene gráficamente en un tablero de a × b casillas, enumerando las casillas de la diagonal (lo que corresponde a la aplicación n → (n, n) ) y cuando se alcanza un borde se sigue por el borde opuesto, como si se tocasen. Las flechas en rojo de la segunda figura indican estos repentinos cambios de bordes.
Miremos por ejemplo la casilla que contiene el número 17. Corresponde al elemento ${\overline {17}}$ de Z₂₈. Está situado en la columna ${\overline {3}}$ y la fila ${\overline {1}}$.
Entonces ${\overline {17}}$ de Z₂₈ corresponde a $({\overline {3}},{\overline {1}})$ de Z₇×Z₄.

Con valores pequeños de a y b existe otra manera de obtener la biyección: En vez de cortar en pedazos la diagonal, se prefiere reproducir el tablero a × b cuantas veces sea necesario (de hecho, b·a veces) para obtener los a·b elementos de Z_a·b. Luego se los reúnen en un mismo cuadro.
Z₆ ≡ Z₂×Z₃, así:
0 → (0,0)
1 → (1,1)
2 → (0,2)
3 → (1,0)
4 → (0,1)
5 → (1,2)

Pegar los bordes opuestos de un rectángulo da en topología un toro, un neumático sin la apertura central. El toro es en geometría el producto de dos círculos, cada uno representa un anillo cíclico.

• El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.

• Datos: Q5695908