Sistema axiomático
En lógica y matemáticas, un sistema axiomático consiste en un conjunto de axiomas que se utilizan, mediante deducciones, para demostrar teoremas. En otras palabras, la idea de un sistema axiomático consiste en dar al principio los axiomas, es decir, las afirmaciones que se aceptan como verdaderas, y después derivar, mediante deducción, todas las afirmaciones. Se debe evitar que los axiomas se puedan deducir a partir de los otros y, además, los axiomas deben ser consistentes.[1] Ejemplos de sistemas axiomáticos deductivos son la geometría euclidiana compilada por Euclides en los Elementos[2] y el sistema axiomático de la lógica proposicional.
Historia[editar]
El primer trabajo, en la historia de la matemática, de axiomatización se desplegó en los Elementos de Euclides (siglo IV-III a. C.), vinculado a la geometría plana y algunos aspectos de la aritmética.[3] Euclides enuncia cinco postulados y cinco nociones comunes (axiomas), de los que deduce sus teoremas de la geometría. Al mismo tiempo, Aristóteles aporta el primer enfoque de la lógica formal en el Órganon, recogiendo diversos axiomas de Platón y otros filósofos.
En matemáticas, sin embargo, el primer intento de axiomatización llegó en 1888, cuando Richard Dedekind propuso un conjunto de axiomas sobre los números.[4] Al año siguiente, Giuseppe Peano retoma los trabajos de Dedekind y expone sus axiomas aritméticos.
Gottlob Frege, en 1884, con su obra Die Grundlagen der Arithmetik y la posterior Grundgesetze der Arithmetik, trata de reducir la aritmética a la lógica. Bertrand Russell en su intento de 1901 descubrió la paradoja del mismo nombre: «paradoja de Russell», y para resolverla trabajó con Alfred North Whitehead, en Principia Mathematica. En 1899, David Hilbert reformula los axiomas de la geometría, y también explica los conceptos que Euclides dejó implícitos, por ejemplo, Euclides no dice que hay al menos tres puntos en el plano, o que hay al menos un punto en el plano que no pertenece a la línea, etc.
En el Congreso celebrado en 1900, David Hilbert planteó varios problemas, entre los que incluía la demostración de la consistencia de los axiomas de las matemáticas y la axiomatización de la física. En 1931, Kurt Gödel demostró que cualquier sistema axiomático equivalente a los axiomas de Peano es incompleto y que si este sistema es consistente, no se puede utilizar para probar su consistencia (teorema de incompletitud de Gödel).
Sistemas axiomáticos formales e informales[editar]
Un sistema axiomático puede tener expresados sus axiomas de manera formal o de manera informal:
- Una axiomatización formal usa un lenguaje formal y en él cada axioma es una cadena finita de signos en el alfabeto del lenguaje formal, siguiendo reglas combinatorias que hacen de la secuencia una fórmula bien formada.
- Una axiomatización informal usa una lengua natural formalizada y definiciones no ambiguas, los libros de matemática y otras disciplinas formales normalmente redactan los axiomas de esta manera.
Los sistemas de axiomas formales son más sencillos de estudiar y son preferibles para caracterizar las propiedades de los sistemas matemáticos. En particular admiten una caracterización semántica muy clara en la teoría de modelos y sus propiedades deductivas pueden ser tratadas en la teoría de la demostración. Por el contrario, las axiomatizaciones informales sólo son útiles cuando se tiene un modelo concreto en mente y se pretenden buscar propiedades que se cumplen en el modelo.
Componentes de un sistema axiomático formal[editar]
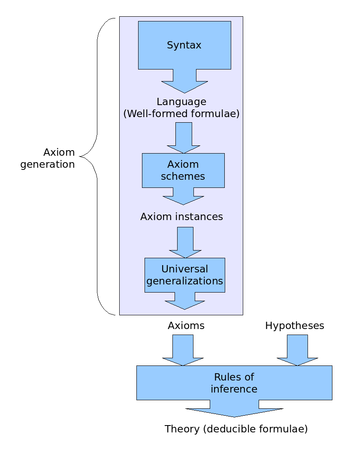
Un sistema axiomático formal consta de los siguientes elementos:
- Un alfabeto S para construir expresiones formales que incluye:
- Un conjunto de símbolos para conectivas lógicas, cuantificadores
- Un conjunto de símbolos para designar variables
- Un conjunto de símbolos para constantes (que tendrán en un modelo una interpretación fija).
- Un conjunto de símbolos que serán interpretados como funciones.
- Un conjunto de símbolos que serán interpretados como relaciones.
- Una gramática formal que incluirá:
- Reglas de buena formación, que reproducen la "morfología" del lenguaje formal.
- Reglas de inferencia que permitirán deducir unas proposiciones de otras, estas reglas reproducen la "sintaxis" del lengua formal.
- Un conjunto de axiomas inicial, o expresiones bien formadas son el punto de partida de cualquier deducción.
Para el conjunto de expresiones bien formadas expresadas en el lenguaje formal anterior puede definirse una S-estructura en la que a cada variable constante o cada ocurrencia libre de una variable reciba un valor dentro del modelo (es decir, las constantes y variables libres serán conjuntos preasignados de la S-estructura). Las funciones y relaciones serán definidas como funciones y relaciones matemáticas dentro de la S-estructura. Una vez definidas las constantes, variables libres, funciones y relaciones resulta trivial atribuir un significado concreto a las expresiones del lenguaje formal en la S-estructura.
Modelos para un sistema axiomático formal[editar]
Si un conjunto de proposiciones (fórmulas bien formadas) de un sistema axiomático formal admiten una S-estructura donde se satisfacen, entonces se dice que dicha estructura es un modelo para el conjunto de proposiciones. Un sistema de axiomas que admite un modelo es un sistema de axiomas consistente. Un sistema formal bien construido satisface el "teorema de validez", que viene a afirmar que cualquier proposición deducible de los axiomas, o teorema del sistema axiomático, se satisface también, en todos los modelos que sean un modelo en el que se satisfacen los axiomas. La propiedad recíproca no siempre se cumple, una proposición que se satisface en todos los modelos de una teoría no tiene porqué ser deducible del sistema de axiomas. Este último punto es ilustrado por los teoremas de incompletitud de Gödel, que afirman que un sistema formal de ciertos sistemas matemáticos con un conjunto de axiomas que satisface determinada propiedad formal (ser un recursivamente enumerables) admitirá un modelo en el que algunas proposiciones serán ciertas pero no serán deducibles. Es decir, la teoría asociada al sistema axiomático formal será esencialmente incompleta.
Ejemplos[editar]
La teoría de grupos es un sistema axiomático se puede basar en el siguiente conjunto de tres axiomas G1, G2 y G3:
- (G1) para todo x, y y z:
- (G2) para todo x:
- (G3) para todo x, existe un y tal que
Este conjunto de axiomas no es único, ya que pueden ser substituidos por otros equivalentes. En teoría de grupos el asunto importante es que el conjunto de teoremas sean los mismos en dos axiomatizaciones diferentes. Eso implica que las dos clases de modelos que satisfacen los dos sistemas de axiomas coindiden. Los tres axiomas anteriores pueden escribirse sin usar ninguna lengua natural usando sólo símbolos de un lenguaje de primer orden como:
- (G1)
- (G2)
- (G3)
Donde f debe interpretarse como la función definida sobre GxG que da un elemento de G dando operación de grupo, xi son signos de variables (puede definirse una colección infinita numerable de las mismas) y c1 es una constante que requiere la teoría que se interpretará como el elemento neutro (es decir, los axiomas postulan que dicho elemento existe).
Características[editar]
- Consistencia
- Independencia
- Completitud
Véase también[editar]
- Proposición
- Axioma
- Postulado
- Definición
- Teorema
- Corolario (matemática)
- Lema ( matemáticas)
- Escolio
- Conceptos primitivos
- Sistema formal
- Axiomas de Hilbert
Referencias[editar]
- ↑ Enciclopedia de conocimientos fundamentales: UNAM-Siglo XXI / coord. Jaime Labastida y Rosaura Ruíz. - México: UNAM ; Siglo xxi, 2010.
- ↑ Sistema axiomático deductivo en symploke
- ↑ por ejemplo cuando se enuncia: " el todo es mayor que una parte
- ↑ Richard Dedekind, 1890, Letter to Keferstein. pp. 98–103.






