Método de las imágenes

El método de las cargas imagen (también conocido como método de las imágenes y método de las cargas espejo) es una herramienta básica para la solución de problemas en electrostática. El nombre se origina del reemplazo de ciertos elementos del problema original por cargas "imaginarias" que replican las condiciones de frontera del problema (ver Problema de condición de frontera).

La validez del método descansa en un corolario del teorema de unicidad, que establece que el potencial eléctrostático en un volumen V está únicamente determinado una vez que se establecen la densidad de carga y el valor del potencial electrostático sobre la frontera de la región. Alternativamente, la aplicación de este corolario a la forma diferencial de la ley de Gauss muestra que en un volumen V rodeado por conductores y conteniendo una densidad de carga $\rho$ especificada, el campo electrostático está unívocamente determinado si la carga total en cada conductor es dada.

Disponiendo del conocimiento sobre el potencial electrostático o el campo electrostático y las correspondientes condiciones de frontera es posible intercambiar la distribución de carga que consideramos por una con una configuración que es más simple de analizar, siempre que satisfaga la ecuación de Poisson en la región de interés, de forma que se obtengan los valores correctos sobre la frontera.​

Reflexión en una placa conductora

El campo de una carga positiva sobre la superficie de una placa conductora plana, calculado por el método de las imágenes.

Método de las imágenes para un momento dipolar eléctrico sobre un plano conductor.

Cargas puntuales

El ejemplo más simple del método de las imágenes es el de una carga puntual, de carga q, localizado en $(0,0,a)$ sobre una placa conductora infinita, conectada a tierra (i.e.: $V=0$) sobre el plano xy. Para simplificar este problema, podemos reemplazar la placa por una carga -q localizada en $(0,0,-a)$. Este arreglo produce el mismo campo eléctrostático en cualquier punto de la región $z>0$ (i.e.: sobre la placa conductora), y satisface la condición de que el potencial sobre la placa se anule. Esta situación es equivalente a la original, de manera que es posible calcular la fuerza sobre la carga real (en $(0,0,a)$) que ejerce la placa mediante la ley de Coulomb entre la carga y su carga imagen.​

El potencial en cualquier punto del espacio, debido a estas dos cargas puntuales de carga +q en +a y -q en -a sobre el eje z, se expresa en coordenadas cilíndricas como $V\left(\rho ,\varphi ,z\right)={\frac {1}{4\pi \epsilon _{0}}}\left({\frac {q}{\sqrt {\rho ^{2}+\left(z-a\right)^{2}}}}+{\frac {-q}{\sqrt {\rho ^{2}+\left(z+a\right)^{2}}}}\right)\,$

La densidad superficial de carga sobre la placa conductora conectada a tierra viene dada entonces por

$\sigma =-\epsilon _{0}{\frac {\partial V}{\partial z}}{\Bigg |}_{z=0}={\frac {-qa}{2\pi \left(\rho ^{2}+a^{2}\right)^{3/2}}}$

Además, la carga total inducida sobre la placa conductora será la integral de esta densidad superficial de carga sobre todo el plano conductor, y por lo tanto,

${\begin{aligned}Q_{t}&=\int _{0}^{2\pi }\int _{0}^{\infty }\sigma \left(\rho \right)\,\rho \,d\rho \,d\varphi \\[6pt]&={\frac {-qa}{2\pi }}\int _{0}^{2\pi }d\varphi \int _{0}^{\infty }{\frac {\rho \,d\rho }{\left(\rho ^{2}+a^{2}\right)^{3/2}}}\\[6pt]&=-q\end{aligned}}$

La carga total inducida sobre el plano resulta ser simplemente –q. Esto puede verse directametente como una consecuencia de la ley de Gauss, considerando que el campo dipolar decae como el cubo de la distancia a grandes distancias, y por lo tanto, el flujo total del campo a través de una superficie hemiesférica infinita se anula.

Como el campo electrostático satisface el principio de superposición, una placa conductora bajo múltiples cargas puntuales puede ser remplazada por las cargas imagen de cada una de las cargas individualmente, sin requererir mayores modificaciones.

Momentos dipolares eléctricos

La imagen de un dipolo eléctrico p en $(0,0,a)$ sobre una placa conductora infinita conectada a tierra localizada sobre el plano xy es un momento dipolar localizado en $(0,0,-a)$ con igual magnitud, rotado en torno al eje azimutal en π. Esto es, un momento dipolar con componentes cartesianas $(p\sin \theta \cos \phi ,p\sin \theta \sin \phi ,p\cos \theta )$ tendrá una imagen con momento dipolar $(-p\sin \theta \cos \phi ,-p\sin \theta \sin \phi ,p\cos \theta )$. El dipolo experimenta entonces una fuerza en la dirección z, dada por:$F=-{\frac {1}{4\pi \epsilon _{0}}}{\frac {3p^{2}}{16a^{4}}}(1+\cos ^{2}\theta )$ y un torque en el plano perpendicular al dipolo y la placa conductora: $\tau =-{\frac {1}{4\pi \epsilon _{0}}}{\frac {p^{2}}{16a^{3}}}\sin 2\theta$

Reflexión en la interfase de un plano dieléctrico

De manera similar al plano conductor, podemos considerar el caso de la interfase entre dos medios dieléctricos. Si una carga puntual $q$ se localiza en un dieléctrico que tiene constante dieléctrica $\epsilon _{1}$, entonces la interfase (con el dieléctrico que tiene constante dieléctrica $\epsilon _{2}$) desarrollará una carga ligada de polarización. Se puede demostrar que el campo eléctrico resultante dentro del dieléctrico que contiene la partícula se modifica de manera que puede describirse mediante una carga imagen dentro del otro dieléctrico. En el interior del segundo dieléctrico, sin embargo, dicha carga no está presente.​

A diferencia del caso del conductor, la carga imagen $q'$ no es exactamente la opuesta a la carga real: $q'={\frac {\epsilon _{1}-\epsilon _{2}}{\epsilon _{1}+\epsilon _{2}}}q$. Incluso, puede tener el mismo signo, si la carga se sitúa en el interior de un material con mayor constante dieléctrica (las regiones con mayor constante dieléctrica repelen a las cargas), lo que se sigue de la fórmula anterior.

Reflexión por una esfera conductora

Diagrama ilustrando el método de las imágenes para la Ecuación de Laplace para una esfera de radio R. El punto verde es una carga q emplazada dentro de la esfera a una distancia p del origen. El punto rojo es la imagen de ese punto, con una carga -qR/p, ubicado fuera de la esfera a una distancia R²/p del origen. El potencial producido por ambas cargas es cero sobre la superficie de la esfera.

Líneas de campo fuera de la esfera conductora conectada a tierra para una carga ubicada fuera de la esfera.

Varias superficies requieren una serie infinita de puntos imagen.

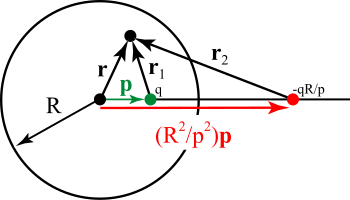
Cargas puntuales

El método de las imágenes puede ser aplicado también a una esfera.​ De hecho, el caso de las cargas imagen en un plano es un caso límite de las imágenes para una esfera. Refiriéndonos a la figura, deseamos encontrar el potencial adentro de una esfera conductora de radio R conectada a tierra, centrada en el origen, debido a una carga fuera de la esfera en la posición $\mathbf {p}$ (Para el caso opuesto, el potencial fuera de la esfera debida a una carga fuera de la de la esfera, el método se aplica de manera similar). En la figura, esto es representado por un punto verde. Sea $q$ la carga ese punto. La imagen de esa carga con respecto a la esfera a tierra es mostrada en rojo. Esta tiene carga $q'=-qR/p$ y se localiza sobre la línea que conecta el centro de la esfera y la carga interior, a una distancia $(R^{2}/p^{2})\mathbf {p}$ del centro de la esfera. Se puede ver que el potencial en un punto especificado por un radio vector $\mathbf {r}$ debido sólo a ambas cargas está dado por la suma de las contribuciones de la carga real y la carga imagen:

$4\pi \epsilon _{0}V(\mathbf {r} )={\frac {q}{|\mathbf {r} _{1}|}}+{\frac {(-qR/p)}{|\mathbf {r} _{2}|}}={\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}+{\frac {(-qR/p)}{\sqrt {r^{2}+{\frac {R^{4}}{p^{2}}}-{\frac {2R^{2}}{p^{2}}}\mathbf {r} \cdot \mathbf {p} }}}$

Multiplicando en la expresión de más a la derecha, se obtiene: $V(\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}-{\frac {q}{\sqrt {{\frac {r^{2}p^{2}}{R^{2}}}+R^{2}-2\mathbf {r} \cdot \mathbf {p} }}}\right]$

y puede verse que sobre la superficie de la esfera, (i.e. cuando $r=R$) el potencial se anula. El potencial dentro de la esfera está de esta manera dado por la expresión de arriba para el potencial de las dos cargas. Nótese que esta expresión NO es válida fuera de al esfera, ya que la carga imagen no existe en realidad, sino que "está ahí" representando a la densidad de carga inducida sobre la esfera por la carga interior en $\mathbf {p}$. El potencial fuera de la esfera quedará determinado solo por la distribución de carga fuera de la esfera y será por lo tanto independiente de la distribución de carga dentro de esta. Si asumimos por simplicidad (sin pérdida de generalidad) que la carga interior yace sobre el eje z, entonces la densidad de carga inducida será una función del ángulo polar θ, dada por:

$\sigma (\theta )=\epsilon _{0}{\frac {\partial V}{\partial r}}{\Bigg |}_{r=R}={\frac {-q(R^{2}-p^{2})}{4\pi R(R^{2}+p^{2}-2pR\cos \theta )^{3/2}}}$

La carga total sobre la esfera puede encontrarse integrando esta densidad superficial sobre todos los ángulos:

$Q_{t}=\int _{0}^{\pi }d\theta \int _{0}^{2\pi }d\phi \,\,\sigma (\theta )R^{2}\sin \theta =-q$

Nótese que el problema recíproco también se resuelve por este método. Si tenemos una carga q en la posición $\mathbf {p}$ fuera de la esfera cargada, el potencial fuera de la esfera es dado por la suma de los potenciales de la carga y su imagen dentro de la esfera. Justo como antes, la carga imagen tendrá un valor de $q'=-qR/p$ y yacerá en $(R^{2}/p^{2})\mathbf {p}$. El potencial dentro de la esfera dependerá sólo de la distribución de carga dentro de la esfera. A diferencia del primer caso, la integral será de valor -qR/p.

Esfera cargada

Consideremos ahora una esfera conductora, pero que ahora en vez de estar conectada a tierra se encuentra aislada, y posee una carga neta Q. Como es una esfera conductora, esta carga neta se distribuirá sobre las interfases de manera que el potencial se mantenga constante. Como la carga se localiza en la interfase, podemos escribir el potencial como la superposición de la solución del problema de la esfera conectada a tierra y la solución del problema con simetría esférica

$V_{Q}({\bf {r}})={\frac {Q-q_{imag}}{4\pi \varepsilon _{0}}}\left\{\;_{{\frac {1}{|\{{\bf {r}}}}|}^{\frac {1}{R}}\;_{|{\bf {r}}|<R}^{|{\vec {r}}|>R}\right.$

con $q_{imag}$ la suma algebraica del valor de las cargas imagen. Para el problema exterior, este resultado puede interpretarse como la introducción de una nueva carga imagen $Q'=Q-q_{imag}$ en el centro de la esfera.

Notemos que entonces, el valor del potencial sobre la esfera queda determinado por la carga $Q'$ según

$\left.V({\bf {r}})\right|_{|{\bf {r}}|=R}={\frac {Q'}{4\pi \varepsilon _{0}R}}$

En el caso de que la carga neta de la esfera sea nula ($Q=0$), $Q'=-q_{imag}$. Podemos interpretar este resultado como que el efecto de la presencia de una carga puntual real $q>0$ localizada en ${\bf {p}}$ induce un momento dipolar sobre la esfera colineal con la recta que pasa por la carga y el centro de la esfera, apuntando hacia el centro de la esfera, y de magnitud $|{\bf {D}}|=qR^{3}/p^{2}$

Método de inversión

El método de las imágenes para una esfera lleva directamente al método de inversión.​ Si tenemos una función armónica de posición$\Phi (r,\theta ,\phi )$ donde $r,\theta ,\phi$ son las coordenadas esféricas de la posición, entonces la imagen de esta función armónica en una esfera de radio R centrada en el origen será

$\Phi '(r,\theta ,\phi )={\frac {R}{r}}\Phi \left({\frac {R^{2}}{r}},\theta ,\phi \right)$

Si el potencial $\Phi$ es el resultado de un conjunto de cargas de magnitud $q_{i}\,$ en posiciones $(r_{i},\theta _{i},\phi _{i})\,$, entonces el potencial imagen será el resultado de una serie de densidades de carga$\rho '(r,\theta ,\phi )=(R/r)^{5}\rho (R^{2}/r,\theta ,\phi )\,$.

Véase también

• Transformada de Kelvin
• Ley de Coulomb
• Teorema de Gauss
• Flujo
• Superficie gaussiana
• Principio de reflexión de Schwarz
• Teorema de unicidad del potencial

Referencias

• Jackson, John D. (1962). Classical Electrodynamics. John Wiley & Sons. 
• Jeans, James H. (1908). The Mathematical Theory of Electricity and Magnetism. Cambridge University Press. 

Otras lecturas

• Feynman, Richard; Leighton, Robert B.; Sands, Matthew (1989). Feynman Lectures on Physics, Mainly Electromagnetism and Matter. Addison-Wesley. ISBN 0-201-51003-0. 
• Landau, Lev D.; Lifshitz, Evgeny M.; Pitaevskii, Lev P. (1960). Electrodynamics of Continuous Media 2nd Edition. London: Elsevier. ISBN 978-0-7506-2634-7. 
• Purcell, Edward M.. Berkeley Physics Course, Vol-2: Electricity and Magnetism (2nd ed.). McGraw-Hill. 

• Datos: Q1372220
• Multimedia: Method of image charges / Q1372220