Teoría de conjuntos

Diagrama de Venn que muestra un conjunto $A$ contenido en otro conjunto $U$ y su complemento $A^{\complement }$

La Teoría de Conjuntos es una división de las matemáticas que estudia los conjuntos. El primer estudio formal sobre el tema fue realizado por el matemático alemán Georg Cantor, Gottlob Frege y Julius Wilhelm Richard Dedekind en el Siglo XIX y más tarde reformulada por Zermelo.

El concepto de conjunto es intuitivo y se podría definir como una "colección de objetos"; así, se puede hablar de un conjunto de personas, ciudades, gafas, lapiceros o del conjunto de objetos que hay en un momento dado encima de una mesa. Un conjunto está bien definido si se sabe si un determinado elemento pertenece o no al conjunto. El conjunto de los bolígrafos azules está bien definido, porque a la vista de un bolígrafo se puede saber si es azul o no. El conjunto de las personas altas no está bien definido, porque a la vista de una persona, no siempre se podrá decir si es alta o no, o puede haber distintas personas, que opinen si esa persona es alta o no lo es. En el siglo XIX, según Frege, los elementos de un conjunto se definían sólo por tal o cual propiedad. Actualmente la teoría de conjuntos está bien definida por el sistema ZFC. Sin embargo, sigue siendo célebre la definición que publicó Cantor.

Se entiende por conjunto a la agrupación en un todo de objetos bien diferenciados de nuestra intuición o nuestra mente.

Georg Cantor

Un conjunto es un saco lleno de elementos. Dentro del saco puede haber números, letras, plantas, personas, mastodontes, ..., prácticamente cualquier cosa.

Julius Wilhelm Richard Dedekind

Notación

Usualmente los conjuntos se representan con una letra mayúscula: $A$, $B$, $K$,...

Llamaremos elemento, a cada uno de los objetos que forman parte de un conjunto, estos elementos tienen carácter individual, tienen cualidades que nos permiten diferenciarlos, y cada uno de ellos es único, no habiendo elementos duplicados o repetidos. Los representaremos con una letra minúscula: $a$, $b$, $k$,...

De esta manera, si $~A$ es un conjunto, y $~a,b,c,d,e$ todos sus elementos, es común escribir:

$~A=\{a,b,c,d,e\}$

para definir a tal conjunto $~A$. Esta notación empleada para definir al conjunto $~A$ se llama notación por extensión.

Para representar que un elemento $~x$ pertenece a un conjunto $A$, escribimos $x\in A$ (léase "$x$ en $A$", "$x$ pertenece a $A$" o bien "$x$ es un elemento de $A$"). La negación de $x\in A$ se escribe $x\notin A$ (léase $~x$ no pertenece a $~A$).

El conjunto universal, que siempre representaremos con la letra $U$ (u mayúscula), es el conjunto de todas las cosas sobre las que estemos tratando. Así, si hablamos de números enteros entonces $U$ es el conjunto de los números enteros, si hablamos de ciudades, $U$ es el conjunto de todas las ciudades, este conjunto universal puede mencionarse explícitamente, o en la mayoría de los casos se da por supuesto dado el contexto que estemos tratando, pero siempre es necesario demostrar la existencia de dicho conjunto previamente.

Existe además, un único conjunto que no tiene elementos al que se le llama conjunto vacío y que se denota por $\emptyset$. Es decir

$\emptyset =\{\}$

La característica importante de este conjunto es que satisface todos los elementos posibles que no están contenidos en él, es decir

$\forall x\quad x\notin \emptyset$.

Por otro lado, si todos los elementos $~x$ de un conjunto $A$ satisfacen alguna propiedad, misma que pueda ser expresada como una proposición $p\left(x\right)$, con la indeterminada $~x$, usamos la notación por comprensión, y se puede definir:

$~A=\{x\in U:p(x)\}$

Lo anterior se lee "$A$ es el conjunto de elementos $x$, que cumplen la propiedad $p(x)$". El símbolo ":" se lee "que cumplen la propiedad" o "tal que"; este símbolo puede ser remplazado por una barra $\mid$.

Por ejemplo, el conjunto $~A=\{1,2,3,4\}$ puede definirse por:

$~A=\{n\in \mathbb {N} :1\leq n\leq 4\}$

donde el símbolo $\mathbb {N}$ representa al conjunto de los números naturales.

Igualdad entre conjuntos. Subconjuntos y Superconjuntos

Igualdad de conjuntos

Dos conjuntos $~A$ y $~B$ se dicen iguales, lo que se escribe $~A=B$ si constan de los mismos elementos. Es decir, si y solo si todo elemento de $A$ está también contenido en $B$ y todo elemento de $B$ está contenido en $A$. En símbolos:

$\forall x,x\in A\iff x\in B$

Subconjuntos y Superconjuntos

Diagrama de Venn que muestra $A\subseteq B$

Un conjunto $~A$ se dice que es subconjunto de otro $~B$, si cada elemento de $~A$ es también elemento de $~B$, es decir, cuando se verifique:

$x\in A\Rightarrow x\in B$,

sea cual sea el elemento $~x$. En tal caso, se escribe $A\subseteq B$.

Cabe señalar que, por definición, no se excluye la posibilidad de que si $A\subseteq B$, se cumpla $A=B\,$. Si $~B$ tiene por lo menos un elemento que no pertenezca al conjunto $~A$, pero si todo elemento de $~A$ es elemento de $~B$, entonces decimos que $~A$ es un subconjunto propio de $~B$, lo que se representa por $A\subset B$. En otras palabras, $A\subset B$ si y sólo si $A\subseteq B$, y $B\setminus A\neq \emptyset$. Así, el conjunto vacío es subconjunto propio de todo conjunto (excepto de sí mismo), y todo conjunto $A$ es subconjunto impropio de sí mismo.

Si $~A$ es un subconjunto de $~B$, decimos también que $~B$ es un superconjunto de $~A$, lo que se escribe $B\supseteq A$. Así pues

$B\supseteq A\iff A\subseteq B$,

y también que:

$B\supset A\iff A\subset B$,

significando $B\supset A$ que $~B$ es superconjunto propio de $~A$.

Por el principio de identidad, es siempre cierto $x\in A\Rightarrow x\in A$, para todo elemento $~x$, por lo que todo conjunto es subconjunto (y también superconjunto) de sí mismo.

Vemos que $\subseteq$ es una relación de orden sobre un conjunto $~S$ de conjuntos, pues

$A\subseteq A$			($\subseteq$ es reflexiva)
$A\subseteq B\wedge B\subseteq A$	$\qquad \Rightarrow \qquad$	$A=B\,$	($\subseteq$ es antisimétrica)
$A\subseteq B\wedge B\subseteq C$	$\qquad \Rightarrow \qquad$	$A\subseteq C$	($\subseteq$ es transitiva)

Operaciones con conjuntos

Sean $~A$ y $~B$ dos conjuntos.

Unión $\cup$

Diagrama de Venn que ilustra $A\cup B$

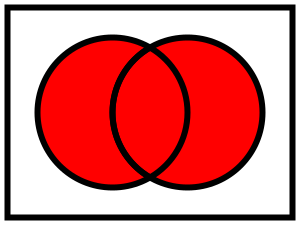
Para cada par de conjuntos $A$ y $B$ existe un conjunto Unión de los dos, que se denota como $A\cup B$ el cual contiene todos los elementos de $A$ y de $B$. De manera más general, para cada conjunto $S$ existe otro conjunto denotado como $\bigcup S$ de manera que sus elementos son todos los $x\in X$ tales que $X\in S$. De esta manera $A\cup B$ es el caso especial donde $S=\{A,B~\}$.

Es claro que el hecho de que un elemento $x$ pertenezca a $A\cup B$ es condición necesaria y suficiente para afirmar que $x$ es un elemento de $A$ o al menos de $B$. Es decir

$x\in (A\cup B)\iff (x\in A)\vee (x\in B)$

Ejemplos: si tenemos los conjuntos

$~A=\{\triangle ,\bigcirc ,6\}$

$~B=\{\star ,6,\dagger ,\square \}$

$~C=\{\square ,14,\star ,\clubsuit \}$

$~S=\{A,B,C\}$

Entonces

$A\cup B=\{\triangle ,\bigcirc ,6,\star ,\dagger ,\square \}$

$A\cup C=\{\triangle ,\bigcirc ,6,\square ,14,\star ,\clubsuit \}$

$\bigcup S=\{\triangle ,\bigcirc ,6,\star ,\dagger ,\square ,14,\clubsuit \}$

$~A\cup \emptyset =A$

$~A\cup A=A$

Intersección n

Diagrama de Venn que ilustra $A\cap B$

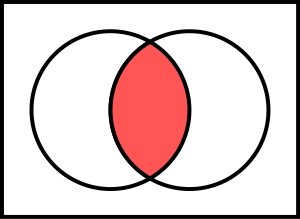
Los elementos comunes a $~A$ y $~B$ forman un conjunto denominado intersección de $~A$ y $~B$, representado por $A\cap B$. Es decir, $A\cap B$ es el conjunto que contiene a todos los elementos de $A$ que al mismo tiempo están en $B$:

$A\cap B=\{x\in A:x\in B\}$.

Si dos conjuntos $~A$ y $~B$ son tales que $A\cap B=\emptyset$, entonces $~A$ y $~B$ se dice que son conjuntos disjuntos.

Es claro que el hecho de que $x\in A\cap B$ es condición necesaria y suficiente para afirmar que $x\in A$ y $x\in B$. Es decir

$x\in (A\cap B)\iff (x\in A)\wedge (x\in B)$

Ejemplos: si tenemos los conjuntos

$~A=\{2,4,6\}$

$~B=\{4,6,8,10\}$

$~C=\{10,14,16,26\}$

Entonces:

$A\cap B=\{4,6\}$

$A\cap C=\emptyset$

$A\cap \emptyset =\emptyset$

$A\cap A=A$

Particiones

Dado un conjunto $A$ y una serie de subconjuntos $Ai$, se dice que $Ai$ son particiones de $A$ cuando la unión de todas es el conjunto $A$, y la intersección de todas es el conjunto vacío. Es decir, que los subconjuntos $Ai$, forman parte del conjunto mas grande denotado $A$.

Diferencia

Diagrama de Venn que muestra $A-B$

Diagrama de Venn que muestra $B-A$

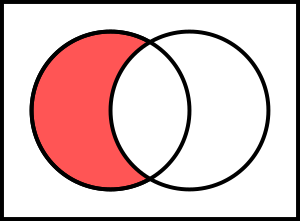
Los elementos de un conjunto $~A$ que no se encuentran en otro conjunto $~B$, forman otro conjunto llamado diferencia de $~A$ y $~B$, representado por $~A\setminus B$. Es decir:

$A\setminus B=\{x\in A:x\notin B\}$.

o dicho de otra manera:

$x\in (A\setminus B)\iff (x\in A)\wedge (x\notin B)$

Algunas personas prefieren denotar la diferencia de $A~$ y $B~$ como $A-B~$.

Una propiedad interesante de la diferencia es que

$A\cap B=A\setminus (A\setminus B)$

eso es porque

${\begin{array}{rcl}x\in A\cap B&\iff &(x\in A)\wedge (x\in B)\\&\iff &(x\in A)\wedge (x\notin A\setminus B)\\&\iff &x\in A\setminus (A\setminus B)\end{array}}$

Ejemplos: Sin importar cual conjunto $A$ elija usted, siempre se cumple

$A\setminus \emptyset =A$

$\emptyset \setminus A=\emptyset$

$\{0,1,2,3\}\setminus \{3,2\}=\{0,1\}$

Complemento

El complemento de un conjunto $A$, es el conjunto de los elementos que pertenecen a algún conjunto $U$ pero no pertenecen a $A$, que lo representaremos por $A^{\complement }$. Es decir

$A^{\complement }=U\setminus A$

El conjunto complemento siempre lo es respecto al conjunto universal que estamos tratando, esto es, si hablamos de números enteros, y definimos el conjunto de los números pares, el conjunto complemento de los números pares, es el formado por los números no pares. Si estamos hablando de personas, y definimos el conjunto de las personas rubias, el conjunto complementario es el de las personas no rubias.

En vista de que $A\subseteq U$ y $B\subseteq U$, entonces

$x\in \left(A\setminus B\right)\iff x\in \left(A\cap B^{\complement }\right)$,

de manera que

$A\setminus B=A\cap B^{\complement }$

Pero también

${\begin{array}{rcl}x\in \left(A\cap B^{\complement }\right)&\iff &x\in A\wedge x\in B^{\complement }\\&\iff &x\in B^{\complement }\wedge \ x\in A\\&\iff &x\in B^{\complement }\wedge x\notin A^{\complement }\\&\iff &x\in \left(B^{\complement }\setminus A^{\complement }\right)\end{array}}$

de modo que

$~A\setminus B=\left(B^{\complement }\setminus A^{\complement }\right)$

Diferencia simétrica

Los elementos de dos conjuntos,A y B a excepción de aquellos que se encuentran en el área de intersección de dichos conjuntos se define la diferencia simétrica.

$B\Delta A=\left(B\setminus A\right)\cup \left(A\setminus B\right)$

Álgebra de conjuntos

Sean $A$, $B$, y $C$ conjuntos cualesquiera y $U$ un conjunto tal que $A\subseteq U$, $B\subseteq U$ y $C\subseteq U$ entonces:

• $A\cap A=A\,$
• $A\cup A=A$
• $A\cap \emptyset =\emptyset$
• $A\cup \emptyset =A$ Elemento neutro de la unión
• $A\cap U=A$ Elemento neutro de la intersección
• $A\cup U=U$
• $A\cap B=B\cap A$ Propiedad conmutativa de la intersección
• $A\cup B=B\cup A$ Propiedad conmutativa de la unión
• $\left(A^{\complement }\right)^{\complement }=A$ Propiedad de Involución.
• $(A\cap B)\cap C=A\cap (B\cap C)$ Propiedad asociativa de la intersección
• $(A\cup B)\cup C=A\cup (B\cup C)$ Propiedad asociativa de la unión
• $A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$ Propiedad distributiva de la intersección
• $A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$ Propiedad distributiva de la unión
• $A\subseteq B\iff A\cap B=A$
• $A\subseteq B\iff A\cup B=B$
• $A\subseteq B\iff B^{\complement }\subseteq A^{\complement }$
• $A\cap B\subseteq A\subseteq A\cup B$

• $C\setminus (A\cap B)=(C\setminus A)\cup (C\setminus B)$
• $C\setminus (A\cup B)=(C\setminus A)\cap (C\setminus B)$
• $C\setminus (B\setminus A)=(A\cap C)\cup (C\setminus B)$
• $(B\setminus A)\cap C=(B\cap C)\setminus A=B\cap (C\setminus A)$
• $(B\setminus A)\cup C=(B\cup C)\setminus (A\setminus C)$
• $A\subseteq B\iff A\setminus B=\emptyset$
• $A\cap B=\emptyset \iff B\setminus A=B$
• $A\setminus A=\emptyset$
• $\emptyset \setminus A=\emptyset$
• $A\setminus \emptyset =A$
• $A\setminus B=A\cap B^{\complement }$
• $(B\setminus A)^{\complement }=A\cup B^{\complement }$
• $U\setminus A=A^{\complement }$
• $A\setminus U=\emptyset$

Producto cartesiano de conjuntos o producto cruz

Un par ordenado de números $\left(x,y\right)$ es tal si los pares $\left(x,y\right)$ y $\left(y,x\right)$ son uno mismo si y sólo si $~x=y$.

Dados dos conjuntos $~A$ y $~B$, definimos al conjunto producto ( o producto cartesiano) de $~A$ y $~B$ (en ese orden), representado por $~A\times B$, como el conjunto

$~A\times B=\{(x,y)\mid \quad x\in A\quad \wedge \quad y\in B\}$

Ejemplo

Sean $~S=\{1,2,3\}$ y $~R=\{a,b,c\}$. Así,

$~S\times R=\{(1,a),(1,b),(1,c),(2,a),(2,b),(2,c),(3,a),(3,b),(3,c)\}$

Ya que el producto cartesiano está formado de pares ordenados (donde el orden de los componentes importa), resulta

$~A\times B=B\times A\qquad \Leftrightarrow \qquad A=B$

Cuantificadores

Los cuantificadores sirven para indicar cuantos elementos de un conjunto dado cumplen con cierta propiedad. Tales cuantificadores son

• El cuantificador universal, representado por $\forall$. Este cuantificador se emplea para afirmar que todos los elementos de un conjunto cumplen con determinada propiedad. Se escribe

$\forall _{x\in A}\quad p(x)$

• El cuantificador existencial se usa para indicar que al menos un elemento de un conjunto $~A$ cumple con una propiedad. Se escribe

$\exists _{x\in A}\quad p(x)$.

Se definen

$\neg (\forall _{x\in A}\quad p(x))\iff \exists _{x\in A}\quad \neg p(x)$

$\neg (\exists _{x\in A}\quad p(x))\iff \forall _{x\in A}\quad \neg p(x)$

Funciones

Sean $~A$ y $~B$ dos conjuntos. Un subconjunto $f\subset A\times B$, se dice aplicación o función de $~A$ en $~B$, lo que se representa por

$f:A\rightarrow B$

siempre que se verifique

• $\forall _{x\in A}\exists _{y\in B}\quad (x,y)\in f$
• $(x,y)\in f\wedge (x,y^{\prime })\in f\Rightarrow y=y^{\prime }$

Si $(x,y)\in f$, el elemento $~y$ se dice imagen de $~x$ por $~f$, y el elemento $~x$ se llama antecedente de $~y$ por $~f$.

Sea una función $f:A\rightarrow B$. Se emplea la notación $~f(x)$ para representar a la imagen de $x\in A$ por $~f$, y por tanto $f(x)\in B$.

Sean las funciones $f:X\rightarrow f(X)$   y   $g:Y\rightarrow g(Y)$. Se define

$f\circ g:\quad x\rightarrow f(g(x))$,

y se dice que $f\circ g$ es el producto de composición de las funciones $~f$ y $~g$.

Sean $f:A\rightarrow B$, $g:B\rightarrow C$ y $h:C\rightarrow D$ tres funciones. Entonces $h(g\circ f)=(h\circ g)\circ f$ .

Para demostrar la igualdad tendremos que probar que tienen el mismo dominio, el mismo codominio, y que sus imágenes son iguales:

$Dom[h\circ (g\circ f)]=Dom(g\circ f)=Dom(f)=A$

$Dom[(h\circ g)\circ f]=Dom(f)=A$

Hemos demostrado que los dominios son iguales.

$Codom[h\circ (g\circ f)]=Codom(h)=D$

$Codom[(h\circ g)\circ f]=Codom(h\circ g)=Codom(h)=D$

También vemos que tienen el mismo codominio, sólo nos queda ver que $[h(g\circ f)](a)=[(h\circ g)\circ f](a)\ \forall a\in A$ :

$[h\circ (g\circ f)](a)=h[(g\circ f)(a)]=h[g(f(a))]$

$[(h\circ g)\circ f](a)=(h\circ g)(f(a))=h[g(f(a))]$

Por lo tanto queda probado que:

$h(g\circ f)=(h\circ g)\circ f$

Véase también

• Teoría axiomática de conjuntos
• Hipótesis del continuo
• Diagrama de Venn
• Conjunto
• Intersección de conjuntos
• Unión de conjuntos
• Diferencia de conjuntos

Bibliografía

1. González Carlomán, Antonio (6 de 2006). Retículo completo de Boole, lógica matemática, teoría de conjuntos (2 edición). Universidad de Oviedo. Servicio de Publicaciones. p. 232. ISBN 978-84-8317-534-7. 
2. Cantor, Georg (11 de 2005). Fundamentos para una teoría general de conjuntos: escritos y correspondencia selecta. Ferreirós Domínguez, José; Gómez-Caminero, Emilio F.; Ferreirós Domínguez, José (1 edición). Editorial Crítica. p. 320. ISBN 978-84-8432-695-3. 
3. Fernández Laguna, Víctor (2 de 2004). Teoría de conjuntos elemental, Bachillerato (2 edición). Anaya. p. 168. ISBN 978-84-667-2614-6. 
4. Climent Coloma, Joan Josep (10 de 2003). Álgebra: teoría de conjuntos y estructuras algebraicas (2 edición). Editorial Club Universitario. p. 512. ISBN 978-84-8454-302-2. 
5. Setó, Jordi (7 de 2002). Teoría elemental de conjuntos (1 edición). Clag S.A. p. 168. ISBN 978-84-921847-6-7. 
6. Arrieche Alvarado, Mario (7 de 2002). Iniciación de la teoría de conjuntos, en la formación de profesores de matemáticas (1 edición). Arrieche Alvarado, Mario Jose. p. 169. ISBN 978-84-607-4774-1. 
7. González Carlomán, Antonio (9 de 2001). Retículo completo de Boole. Lógica matemática teoría de conjuntos (1 edición). Universidad de Oviedo. Servicio de Publicaciones. p. 204. ISBN 978-84-8317-264-3. 
8. Climent Coloma, Joan Josep (6 de 2001). Álgebra. Teoría de conjuntos y estructuras algebraicas (1 edición). Editorial Club Universitario. p. 240. ISBN 978-84-8454-081-6. 
9. Alonso Jiménez, José A; Pérez Jiménez, Mario de J.; Ruiz Reina, José L. (9 de 1998). Teoría de conjuntos (1 edición). Ediciones La Ñ, S.L. p. 348. ISBN 978-84-89524-45-3. 
10. Hernández Hernández, Fernando (1998). Teoría de conjuntos. México D.F.: Sociedad Matemática Mexicana. 
11. Jonsonbaugh, Richard (2005). Matemáticas Discretas Sexta Edición. Pearson Educación, México, 2005. ISBN 970-26-0637-3. 

Enlaces externos

• Wikimedia Commons alberga una galería multimedia sobre Teoría de conjuntos.