Anexo:Grupos finitos de orden bajo
Este artículo muestra una lista matemática de los grupos finitos de orden bajo (una cardinalidad de hasta 16 elementos) clasificados por isomorfismo de grupos.
Con esta lista se puede determinar de qué grupo conocido es isomorfo un grupo finito G dado: Buscar primero el orden de G, seguidamente busque los candidatos para ese orden en la lista. Si sabe si G es o no es abeliano quizás puede descartar algunos candidatos. Para distinguir entre los candidatos restantes se puede mirar el orden de los elementos de G y compararlos con el orden de los elementos de los candidatos.
Terminología[editar]
El signo de igualdad "=" denota isomorfismo de grupos.
- Zn: el grupo cíclico de orden n (a menudo se utiliza la notación Cn, es isomorfico de Z/nZ).
- Dihn: el grupo diédrico de orden 2n (a menudo se utiliza la notación Dn or D2n)
- Sn: el grupo simétrico de orden n, que contiene las n! permutaciones de un conjunto de n elementos.
- An: el grupo alternado de orden n, que contiene las n!/2 permutaciones pares de n elementos.
- Dicn: the grupo diciclico de orden 4n.
La notación G × H indica el producto directo de dos grupos; Gn indica el producto directo de un grupo consigo mismo n veces. significa el producto semidirecto donde H actúa sobre G, si la acción particular de H sobre G se omite es que todas las acciones no triviales posibles dan el mismo grupo producto salvo el isomorfismo.
Se indican los que son grupos abelianos y los que son grupos simples. (Para los grupos de orden n <60, los grupos simples son exactamente los grupos cíclicos Cn, siendo n primo).
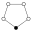
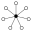
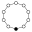
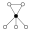
El elemento neutro está representado por un círculo negro en el grafos de los ciclos. El orden más pequeño para el cual el grafo no representa unívocamente un grupo es el orden 16.
En las listas de subgrupos, el grupo trivial y el propio grupo no aparecen indicados. En los casos donde hay múltiples subgrupos isomorfos, el número de apariciones se indica entre paréntesis.
Lista de grupos abelianos pequeños[editar]
Los grupos abelianos finitos se clasifican fácilmente: son grupos cíclicos o sus productos directos. El teorema chino del resto nos puede ayudar a encontrar los isomorfismos con estos productos directos. Los grupos abelianos finitamente generados también se pueden clasificar. Ver más información en el artículo grupo abeliano.
| Orden | Grupo | Subgrupos | Propiedades | Grafo de los ciclos |
|---|---|---|---|---|
| 1 | grupo trivial = Z1 = S1 = A2 | - | Trivialmente tiene propiedades diversas | |
| 2 | Z2 = S2 = Dih1 | - | Simple, el grupo no trivial más pequeño | |
| 3 | Z3 = A3 | - | Simple | |
| 4 | Z4 | Z2 | ||
| Grupo de Klein = Z2 × Z2 = Dih2 | Z2 (3) | El grupo acíclico más pequeño | ||
| 5 | Z5 | - | Simple | |
| 6 | Z6 = Z3 × Z2 | Z3 , Z2 | ||
| 7 | Z7 | - | Simple | |
| 8 | Z8 | Z4 , Z2 | ||
| Z4 × Z2 | Z22, Z4 (2), Z2 (3) | |||
| Z23 | Z22 (7) , Z2 (7) | Los elementos, excepto el neutro, se corresponden con los puntos en el plano de Fano, los subgrupos Z2 x Z2 a las líneas. | ||
| 9 | Z9 | Z3 | ||
| Z32 | Z3 (4) | |||
| 10 | Z10 = Z5 × Z2 | Z5 , Z2 | ||
| 11 | Z11 | - | Simple | |
| 12 | Z12 = Z4 × Z3 | Z6 , Z4 , Z3 , Z2 |  | |
| Z6 × Z2 = Z3 × Z22 | Z6 (3), Z3, Z2 (3), Z22 |  | ||
| 13 | Z13 | - | Simple |  |
| 14 | Z14 = Z7 × Z2 | Z7 , Z2 |  | |
| 15 | Z15 = Z5 × Z3 | Z5 , Z3 | 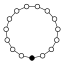 | |
| 16 | Z16 | Z8 , Z4, Z2 |  | |
| Z24 | Z2 (15) , Z22 (35) , Z23 (15) |  | ||
| Z4 × Z22 | Z2 (7) , Z4 (4) , Z22 (7) , Z23, Z4 × Z2 (6) |  | ||
| Z8 × Z2 | Z2 (3) , Z4 (2) , Z22, Z8 (2) , Z4 × Z2 |  | ||
| Z42 | Z2 (3), Z4 (6) , Z22, Z4 × Z2 (3) |  |
Lista de grupos no abelianos pequeños[editar]
| Orden | Grupo | Subgrupos | Propiedades | Grafo de los ciclos |
|---|---|---|---|---|
| 6 | S3 = Dih3 | Z3 , Z2 (3) | El grupo no abeliano más pequeño | |
| 8 | Dih4 | Z4, Z22 (2) , Z2 (5) | ||
| Grupo de los cuaterniones, Q8 = Dic2 | Z4 (3), Z2 | El más pequeño grupo Hamiltoniano; el grupo más pequeño que demuestra que todos los subgrupos pueden ser normales sin que el grupo sea abeliano;el grupo G más pequeño que demuestra que para un subgrupo normal H el grupo cociente G / H no tiene que ser isomorfo a un subgrupo de G | ||
| 10 | Dih5 | Z5 , Z2 (5) | ||
| 12 | Dih6 = Dih3 × Z2 | Z6 , Dih3 (2) , Z22 (3) , Z3 , Z2 (7) |  |
|
| A4 | Z22 , Z3 (4) , Z2 (3) | Grupo más pequeño que demuestra que un grupo no necesita tener un subgrupo de cada orden que divida al orden del grupo, ya que no tiene ningún subgrupo de orden 6 (Ver el teorema de Lagrange y los teoremas de Sylow) |  |
|
| Dic3 = Z3 Z4 | Z2, Z3, Z4 (3), Z6 |  |
||
| 14 | Dih7 | Z7, Z2 (7) |  |
|
| 16 [1] | Dih8 | Z8, Dih4 (2), Z22 (4), Z4, Z2 (9) |  |
|
| Dih4 × Z2 | Dih4 (2), Z4 × Z2, Z23 (2), Z22 (11), Z4 (2), Z2 (11) |  |
||
| Grupo generalizado de los cuaterniones, Q16 = Dic4 |  |
|||
| Q8 × Z2 | Hamiltoniano | 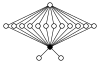 |
||
| El grupo cuasidiedrico de orden 16 | 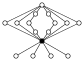 |
|||
| Grupo modular o grupo de Iwasawa de orden 16 |  |
|||
| Z4 Z4 |  |
|||
| El grupo generado por las matrices de Pauli |  |
|||
| G4,4 = Z22 Z4 |  |
Biblioteca de grupos pequeños[editar]
Los sistemas computacionales algebraicos de teoría de grupos GAP y Magma contienen la «Biblioteca de grupos pequeños" que proporciona acceso a descripciones de grupos de orden bajo. Se listan los grupos salvo isomorfismo. Actualmente esta librería contiene los siguientes grupos [2]
- Todos los grupos de orden hasta 2000, excepto los de orden 1024. Son 423.164.062 grupos. Los de orden 1024 no aparecen, sólo contando los 2-grupos de orden 1024 no isomorfos hay 49.487.365.422.
- Los de un orden libre de cubos hasta el 50.000. Son 395.703 grupos.
- Los de un orden libre de cuadrados.
- Los de orden pnpara n hasta 6 y p un número primo.
- Los de orden p7 para p siendo 3, 5, 7 o 11. Son 907.489 grupos.
- Los de orden qn×p donde qn divide a 28, 36, 55 o 74 y el número p es un primo arbitrario diferente de q.
- Aquellos cuyo orden tiene como máximo tres factores primos.
Contiene descripciones explícitas de los grupos disponibles en formato legible por ordenador.
Véase también[editar]
- Grupo (matemáticas)
- Teoría de grupos
- Grupos finitos
- Grupo simple
- Anexo:Pequeños cuadrados latinos y cuasigrupos
Referencias[editar]
- ↑ Wild, Marcel (Enero de 2005). «The Groups of Order Sixteen Made Easy» (pdf). En Asociación Matemática Americana, ed. American Mathematical Monthly (en inglés).
- ↑ Besche, Hans Ulrich; Eick, Bettina y O'Brien, Eamonn. «The Small Groups library» (en inglés). Consultado el 30 de octubre de 2011.
Enlaces externos[editar]
«Particular groups». groupprops.subwiki.org (en inglés). Consultado el 30 de octubre de 2011.
Besche, Hans Ulrich; Eick, Bettina y O'Brien, Eamonn. «The Small Groups library» (en inglés). Consultado el 30 de octubre de 2011.
Hall, Jr, Marshall; Senior, James K. (1964). Macmillan, ed. The Groups of Order 2n (n ≤ 6) (en inglés). LCCN 64016861, MR 168631. «Un catálogo exhaustivo de los 340 grupos con orden divisor de 64 con tablas detalladas de la definición de relaciones, constantes, y presentaciones de retículo de cada grupo; en el prólogo se cita "De un valor duradero para los interesados en los grupos finitos".»
- Esta obra contiene una traducción derivada de «Llista de grups petits» de Wikipedia en catalán, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.