Efecto Sagnac
El efecto Sagnac, también conocido como interferencia de Sagnac, llamado así en honor del físico francés Georges Sagnac, es un fenómeno interferométrico asociado al movimiento de rotación. Se manifiesta en una configuración denominada interferometría de anillo: un haz de luz se divide en dos rayos que siguen trayectorias en direcciones opuestas. Para actuar como un anillo, la trayectoria de la luz debe rodear un área, volver al punto de entrada y formar un patrón de interferencia al salir del aparato. La posición de las franjas de interferencia depende de la velocidad angular de la instalación. Esta disposición también se llama un interferómetro de Sagnac. El efecto Sagnac es el equivalente electromagnético de la mecánica de rotación.
Un giroscopio montado sobre una suspensión Cardán sigue apuntando en la misma dirección aunque gire la base sobre la que esté montado, siendo utilizado como referencia para un sistema de guía inercial. El interferómetro Sagnac mide su velocidad angular con respecto a su sistema de referencia inercial local. Por lo tanto, al igual que el giroscopio también puede proporcionar una referencia para un sistema de guía inercial. Sin embargo, los principios físicos en los que se basan los dos dispositivos son diferentes: el giroscopio utiliza el principio de conservación del momento angular, mientras que el interferómetro se ve afectado por fenómenos relativistas.[cita requerida]
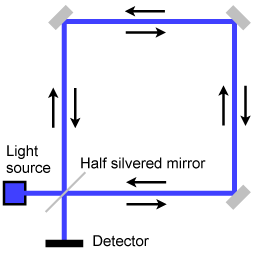
Descripción y funcionamiento[editar]

Generalmente se utilizan varios espejos para que los rayos de luz sigan una trayectoria triangular o cuadrada. La fibra óptica también se puede emplear para dirigir la luz. El interferómetro de anillo está situado en una plataforma que puede girar. Cuando la plataforma está girando, las líneas del patrón de interferencia son desplazadas en comparación con la posición del patrón de interferencia cuando la plataforma no gira. La cantidad de desplazamiento es proporcional a la velocidad angular de la plataforma giratoria. El eje de rotación puede no estar dentro del recinto recorrido por la luz.
Cuando la plataforma está girando, el punto de entrada y el punto de salida se mueven durante el tiempo de tránsito de la luz. En consecuencia, un rayo ha cubierto menos distancia que el otro, lo que crea el cambio en el patrón de interferencia. Por lo tanto, se obtendrá un patrón de interferencia (en función de las características de la plataforma) con un particular desplazamiento de fase propio de cada velocidad angular.
En esta descripción, la velocidad de rotación mencionada siempre se mide con respecto a un marco de referencia inercial.[cita requerida]
Historia[editar]
En teoría, la primera sugerencia para llevar a cabo el experimento de interferometría fue hecha por el físico británico Oliver Joseph Lodge en 1897 y más tarde por el estadounidense Albert Abraham Michelson en 1904. Esperaban que si se podía realizar tal experimento (cuyo objetivo era medir la rotación de la tierra por medios ópticos), sería posible probar o refutar las ideas relativas a la inmovilidad del éter o al completo arrastre del éter por la Tierra. Es decir, si el éter se moviese con la tierra (o con el interferómetro) el resultado sería negativo, mientras que un éter estacionario daría un resultado positivo. [1] [2] [3] Max von Laue en 1911 continuó el trabajo teórico de Michelson y también incorporó la relatividad especial en sus cálculos. Predijo un resultado positivo (de primer orden en v/c) tanto en el supuesto de la relatividad especial como en el del éter estacionario, porque en esas teorías, la velocidad de la luz es independiente de la velocidad de la fuente, y por lo tanto, el tiempo de propagación de los rayos no es el mismo visto desde los dos sistemas de referencia inerciales; sólo el modelo de arrastre completo del éter daría un resultado negativo.[4][5] Mientras Laue limitó sus investigaciones a los sistemas de referencia inerciales, Paul Langevin (1921/35) y muchos otros describieron el efecto desde los propios sistemas de referencia en rotación (analizando los sistemas de coordenadas asociados a la relatividad especial y general).[6][7]
En la práctica, el primer experimento de interferometría destinado a observar la correlación entre velocidad angular y desplazamiento de fase fue realizado por el francés Georges Sagnac en 1913, razón por la cual el efecto lleva su nombre. Su propósito era detectar "el efecto del movimiento relativo del éter".[8][9] Sagnac sólo mencionó la consistencia del experimento con un éter estacionario. Sin embargo, como ya se ha explicado, dos años antes Max von Laue ya predijo este efecto sobre la base de la relatividad especial, por lo que este efecto es consistente con la relatividad especial.[4] El experimento realizado en 1911 por Franz Harress, encaminado a realizar mediciones del coeficiente de arrastre de propagación de Fresnel del movimiento de la luz a través del vidrio, en 1920 fue reconocido por Laue como un experimento de Sagnac. Harress no había atribuido el "sesgo inesperado" del resultado de su experimento a motivos relativistas.[10]
En 1926 se desarrolló un ambicioso experimento de interferometría de anillo dirigido por Albert Michelson y Henry Gale. El objetivo era averiguar si la rotación de la Tierra tiene un efecto sobre la propagación de la luz en las proximidades de su superficie. El experimento de Michelson-Gale-Pearson utilizaba un interferómetro de anillo muy grande (con un perímetro de 1,9 kilómetros), lo suficientemente grande como para detectar la velocidad angular de la tierra. El resultado del experimento fue la confirmación de la exactitud de la medición de la velocidad angular de la Tierra calculada hasta entonces de acuerdo con procedimientos astronómicos. El interferómetro del anillo del experimento de Michelson-Gale no pudo ser calibrado en comparación con una referencia externa (lo que no fue posible, porque la instalación estaba fijada sobre la propia Tierra). A partir de su diseño, se podría deducir donde debería estar la franja de interferencia central si la Tierra no girase. El desplazamiento medido fue 230 partes sobre 1000, con una precisión de 5 partes en 1000. El cambio previsto era de 237 partes en 1000.[11]
Teoría[editar]

El cambio en las franjas de interferencia puede ser visto simplemente como consecuencia de las diferentes distancias que la luz viaja debido a la rotación del observador. La deducción más simple es para un anillo circular que gira a una velocidad angular , pero el resultado es general para las geometrías de lazo con otras formas. Si una fuente de luz emite dos rayos en direcciones opuestas desde un punto en el anillo giratorio, el rayo que viaja a favor del sentido de rotación, se desplaza algo más de una circunferencia completa alrededor del anillo, incidiendo en la pantalla del interferómetro (con un ligero retraso en relación con el rayo opuesto) después de un tiempo
es la distancia (flecha negra regruesada en la figura) que el espejo se ha movido en ese mismo tiempo:
Eliminando de las dos ecuaciones anteriores obtenemos:
Asimismo, la luz que viaja contra la rotación, recorrerá algo menos de una circunferencia antes de alcanzar la fuente de luz en la parte delantera. Así, el tiempo necesario para que el rayo en esta dirección alcance de nuevo la fuente de luz en movimiento se calcula como:
La diferencia de tiempo
Con esto se reduce a
donde A es el área del anillo. Este resultado pasa a ser general para cualquier forma de lazo con el área A.[cita requerida]

El patrón de interferencia se observa mediante una pantalla situada junto a la fuente de luz (o utilizando un divisor de haz para enviar la luz desde el punto de origen a la pantalla). Si la luz se envíase con pulsos más cortos que , no habría ninguna interferencia. Pero las aplicaciones usan luz constante, y el desplazamiento de las franjas de interferencia deben a la presencia de dos haces de luz que llegan a la pantalla en diferentes momentos, y por lo tanto tienen diferentes fases, produciendo interferencias constructivas o destructivas (un patrón de líneas blancas y negras). El cambio de fase es , que hace que las franjas se modifiquen en relación con y .[cita requerida]
En el caso de la luz en el vacío la física prerrelativista y física relativista predicen lo mismo. En otras palabras, en el caso de propagación en el vacío el experimento de Sagnac no distingue entre ambas concepciones teóricas.[cita requerida]
Cuando la luz se propaga en un cable de fibra óptica, la configuración más eficaz es una combinación del experimento de Sagnac y del experimento de Fizeau. En vidrio, la velocidad de la luz es más lenta que en el vacío, y el cable óptico es el medio en movimiento. En este caso se aplica la regla de la adición de velocidad relativista. Teorías Prerrelativistas de la propagación de la luz no pueden explicar el efecto de Fizeau. (Hacia 1900 Lorentz pudo explicar este fenómeno, pero en ese momento su teoría era un conjunto de fórmulas para jusstificarlo, matemáticamente equivalentes a la posterior relatividad especial de Einstein).[cita requerida]
Un reloj conectado al anillo iría más lento debido a su velocidad que el de un observador inercial, lo que redundaría en un aumento de la frecuencia de la luz percibida de la fuente en movimiento por el observador inercial para cancelar este efecto.[cita requerida]
Como el emisor y el receptor viajan a la misma velocidad, el efecto Doppler se cancela en el experimento de Sagnac. En el caso de un anillo de interferometría láser, es importante ser conscientes de ello. Cuando la configuración del anillo láser está girando, los dos rayos experimentan cambios de frecuencia en sentidos opuestos. Este cambio de frecuencia no es un efecto Doppler.[cita requerida]
Marcos de referencia[editar]
El efecto Sagnac no está afectado por la elección del marco de referencia. Es independiente de la elección de marco de referencia, como se puede deducir de su cálculo mediante un tensor métrico: tanto para un observador en el eje de rotación del interferómetro de anillo, como para uno en rotación, dan el mismo resultado. Si se utiliza la métrica de Minkowski y se hacen las conversiones de coordenadas y , (coordenadas de Born) el elemento lineal de la métrica resultante es
donde
- es el tiempo del observador central,
- es la distancia desde el centro,
- es la distancia angular a lo largo del anillo de la dirección que el observador central divisa,
- es la dirección perpendicular al plano del anillo, y
- es la velocidad de rotación del anillo y el observador.
Bajo esta disposición, la velocidad de la luz tangente al anillo es dependiendo de si la luz está en movimiento contra o a favor de la rotación del anillo. Téngase en cuenta que sólo en el caso de es inercial. Para este marco de referencia es no inercial, razón por la cual la velocidad de la luz en posiciones distantes del observador (en ) puede ser distinta de .[cita requerida]
Procedimientos de sincronización[editar]
Los procedimientos para la sincronización de relojes de todo el mundo deben tener la rotación de la Tierra en cuenta. Las señales utilizadas para el procedimiento de sincronización pueden ser en forma de impulsos eléctricos en cables de cobre, pueden ser realizados en cables de fibra óptica de pulsos de luz, o pueden ser señales de radio.[cita requerida]
Si una serie de estaciones repetidoras situadas en el Ecuador se transmitiesen pulsos consecutivamente para sincronizar su hora, ¿el tiempo de referencia aún coincidirá después de que la señal circunnavegase el globo? Una condición para considerar correctamente el efecto de la repetición es tener en cuenta el tiempo que tarda la señal en viajar de una estación a la siguiente. En un planeta sin rotación, esta consideración sería suficiente: dos señales horarias enviadas en sentido contrario van a recorrer el círculo completo exactamente en el mismo tiempo, llegando a la estación de origen simultáneamente. Sin embargo, en un planeta con rotación, también se debe tener en cuenta que el receptor se mueve durante el tiempo de transmisión de la señal, acortando o alargando el tiempo de recepción en comparación con la situación de un planeta sin rotación.[cita requerida]
La sincronización de relojes y la interferometría de anillo están relacionadas de manera fundamental. Por lo tanto, la necesidad de tener en cuenta la rotación de la Tierra en los procedimientos de sincronización también se denomina efecto Sagnac.
Efecto Sagnac en el movimiento de traslación[editar]
En las configuraciones mostradas anteriormente, los segmentos de las rutas de propagación de la luz están en rotación. Experimentos recientes demuestran que existe una diferencia de tiempo de viaje entre dos rayos de luz propagándose en sentido contrario en un segmento de fibra de longitud ΔL moviéndose a una velocidad v (en relación con el marco inercial donde el interferómetro esté momentáneamente en reposo), tanto si el movimiento es de traslación uniforme como si está en rotación en un bucle.[12]
El hallazgo muestra que el efecto Sagnac de rotación
- ,
es un caso especial del Efecto Sagnac Generalizado
donde L es la longitud total de propagación de la luz proyectada en la dirección del movimiento.
La diferencia en el tiempo de recorrido es independiente del índice de refracción del medio. Se sugiere un nuevo sensor de fibra óptica basado en el efecto Sagnac generalizado para medir el movimiento de traslación con una alta sensibilidad.[13]
Usos prácticos[editar]
El efecto Sagnac se emplea en la tecnología actual. Un uso es en el sistema de guía inercial. Los giróscopos de anillo láser son extremadamente sensibles a las rotaciones, pero deben referirse a un sistema de referencia general para devolver resultados precisos si son utilizados en sistemas de guía inercial. El anillo láser también se puede utilizar para detectar el día sideral, que también puede denominarse "modo 1". Los sistemas de navegación global, tales como GPS, GLONASS, COMPASS o el Sistema de navegación Galileo, necesitan tener en consideración la rotación de la Tierra para ajustar las señales de radio utilizadas para sincronizar sus sistemas de relojes.[cita requerida]
Láseres de anillo[editar]

El tipo de interferómetro de anillo descrito a veces se denomina 'interferómetro de anillo pasivo'. Un interferómetro de anillo pasivo utiliza luz que entra al dispositivo desde el exterior. El patrón de interferencia que se obtiene es una franja, y lo que se mide es un desplazamiento de fase.[cita requerida]
También es posible construir un interferómetro de anillo autónomo, basado en una configuración diferente, denominado "anillo láser". La luz es generada y mantenida mediante la incorporación de un láser de excitación en el recorrido de la luz.[cita requerida]
Para entender lo que ocurre en la cavidad del láser del anillo, es útil examinar la física del proceso láser en un dispositivo con generación continua de luz. Cuando se inicia la excitación láser, las moléculas dentro de la cavidad emiten fotones, pero como tienen una determinada excitación térmica, la luz generada dentro de la cavidad del láser se sitúa en una gama de frecuencias correspondiente a la distribución estadística de las velocidades de las moléculas excitadas. El proceso de emisión estimulada consigue que una frecuencia se imponga rápidamente a las otras frecuencias, emitiéndose una luz que está muy próxima de ser monocromática.[cita requerida]

Por simplicidad, se asume que todos los fotones emitidos son emitidos en una dirección tangencial al anillo. (de hecho, es una simplificación enorme, pero sirve muy bien a la explicación).[cita requerida]
La imagen de 'cambio de frecuencia' ilustra el efecto de rotación del anillo de láser.[cita requerida]
En un láser lineal, la luz que se genera se ajusta a la longitud de la cavidad láser exactamente; un múltiplo entero de la longitud de onda se ajusta a la longitud de la cavidad del láser. Esto significa que en el viaje de ida y vuelta, el láser pasa a través de un número entero de ciclos de su frecuencia. En el caso de un anillo láser se aplica el mismo principio: el número de ciclos de frecuencia de la luz láser es el mismo en ambas direcciones. Esta propiedad de tener el mismo número de ciclos en ambas direcciones se conserva cuando el anillo láser está girando. La imagen ilustra que hay cambio de longitud de onda (y por lo tanto, cambio de frecuencia) de tal manera que el número de ciclos es el mismo en ambos sentidos de propagación.[cita requerida]
Uniendo los dos rayos láser, ahora con dos frecuencias ligeramente distintas, puede detectarse un fenómeno de interferencia entre ellas, denominado batimiento (el batimiento es la diferencia entre las dos frecuencias). Este batimiento puede considerarse como un patrón de interferencia en el tiempo. (Las franjas de interferencia más familiares en interferometría son un patrón espacial). El período de esta frecuencia de pulsación es linealmente proporcional a la velocidad angular del anillo láser con respecto al espacio inercial.[cita requerida]
Auto calibrado[editar]

En contraste con el caso de la interferometría de anillo pasivo, en el caso de la interferometría láser de anillo no es necesario proceder a su calibración. Con la interferometría de anillo pasivo, es necesario establecer la posición de las franjas de interferencia que corresponden a la velocidad angular cero (y con la Tierra en rotación, no es posible hacerlo de forma directa). En la interferometría láser de anillo, por el contrario, el dispositivo se está autocalibrando constantemente. El batimiento será cero si y sólo si la configuración del anillo láser no gira con respecto al espacio inercial.[cita requerida]
La animación 'propagación de fotones' ilustra la propiedad física que hace del interferómetro láser de anillo un proceso autocalibrado. Los puntos grises representan moléculas en la cavidad láser que actúan como resonadores. A lo largo de cada sección de la cavidad del anillo, la velocidad de la luz es la misma en ambas direcciones. Cuando el dispositivo láser de anillo está girando, estas moléculas giran con respecto al fondo. En otras palabras: la invariancia de la velocidad de la luz es la referencia para la propiedad del autocalibrado del interferómetro de láser de anillo.[cita requerida]
Bloqueo[editar]
Los giroscopios de anillo láser sufren un efecto conocido como el "lock-in" para velocidades de rotación lentas (inferiores a 100°/hora). Cuando el anillo láser apenas está girando, los modos de las frecuencias de los dos rayos son casi idénticos. En este caso, la interferencia entre los rayos propagados puede provocar el bloqueo del dispositivo, puesto que la reinyección de luz se queda "fijada" en una fase determinada, por lo que las frecuencias de cada rayo se bloquean mutuamente, en lugar de responder a la rotación gradualmente. Para evitar este problema, se suele introducir un movimiento distorsionador en la cavidad del láser (de unos cientos de hercios atrás y adelante, en un ángulo muy pequeño), limitando el problema a los mínimos intervalos en los que su velocidad angular es próxima a cero. La distorsiones producidas por esta corrección tienden a cancelarse entre sucesivos intervalos muertos.[cita requerida]
Detección de ondas gravitacionales. Interferómetro de Sagnac de Área Cero[editar]
La topología del dispositivo de Sagnac en realidad fue descrita por primera vez por Michelson en 1886,[14] que empleó una variante de este interferómetro con un número par de espejos en una repetición del experimento de Fizeau.[15] Michelson se dio cuenta de la extrema estabilidad de las franjas del patrón lumínico producidas por esta forma de interferómetro: franjas de luz blanca se observaron inmediatamente después de la alineación de los espejos. En interferómetros de doble trayectoria, las franjas de luz blanca son difíciles de obtener, ya que las dos longitudes de las trayectoria deben ser exactamente de la misma longitud con una precisión de un par de micrómetros (de acuerdo con la longitud de coherencia de la luz blanca). En la configuración de Sagnac coinciden inherentemente las dos longitudes de trayectoria, al ser un interferómetro de trayecto común. Del mismo modo, Michelson también observó que el patrón de franjas permanecería estable incluso mientras mantenía una cerilla encendida junto bajo la trayectoria óptica (en la mayoría de interferómetros, las franjas se desplazarían en este caso violentamente debido a las fluctuaciones del índice de refracción del aire caliente por encima de la cerilla). Los interferómetros Sagnac son casi insensibles por completo a desplazamientos de los espejos o del divisor del haz de luz.[16] Esta característica de la topología de Sagnac ha conducido a su uso en aplicaciones que requieren una estabilidad excepcionalmente alta.

El desplazamiento de las franjas en un interferómetro de Sagnac debido a la rotación tiene una magnitud proporcional a la zona cerrada de la trayectoria de la luz, y el signo de esta área debe ser especificado en relación con el eje de rotación. Por lo tanto, la señal de la zona de un bucle se invierte cuando el bucle se enrolla en la dirección opuesta (en sentido horario o en sentido antihorario). Una trayectoria de la luz que incluye bucles en ambos sentidos, por lo tanto, tiene una superficie neta dada por la diferencia entre las áreas de los bucles en sentido horario y los de sentido contrario. El caso especial de un interferómetro de Sagnac dos bucles iguales pero opuestos, se denomina en inglés Zero-área (de Área-Cero). El resultado es un interferómetro que presenta la estabilidad de la topología de Sagnac, mientras que es insensible a las rotaciones.[17]
El Laser Interferometer Gravitational-Wave Observatory (LIGO) consiste en dos interferómetros Michelson-Fabry-Pérot de 4 km, y opera con un láser de unos 100 vatios de potencia en el divisor de haz. Una actualización prevista para el LIGO Avanzado requerirá varios kilovatios de potencia del láser, y los científicos tendrán que hacer frente a la distorsión térmica, a la variación de la frecuencia de los láseres, al desplazamiento de los espejos y a la birrefringencia inducida térmicamente.[17]
Una variedad de sistemas ópticos optimizados se están explorando para las mejoras de la tercera generación avanzada del LIGO.[18] Una de estas propuestas se basa en el diseño de un interferómetro de Sagnac de "Área-Cero". Con una trayectoria de la luz que consta de dos bucles de la misma área, pero en direcciones opuestas, se obtiene una superficie efectiva nula, eliminando de esta manera el efecto Sagnac en su sentido usual. Una vez que se hubiese garantizado su insensibilidad a la deriva de baja frecuencia del espejo, a la variación de frecuencia del láser, al desequilibrio de la reflectividad entre los brazos, y a la birrefringencia inducida térmicamente, esta configuración sin embargo debe ser sensible al paso de ondas gravitacionales en las frecuencias de interés astronómico.[17] Sin embargo, muchas consideraciones están todavía implicadas en la elección de un sistema óptico, y a pesar de la superioridad del sistema Sagnac de Área-Cero en ciertos aspectos, no hay hasta ahora ninguna opción de consenso sobre el sistema óptico del LIGO de tercera generación.[19][20]
Véase también[editar]
Referencias[editar]
- ↑ Anderson, R., Bilger, H.R., Stedman, G.E. (1994). «Sagnac effect: A century of Earth-rotated interferometers». Am. J. Phys. 62 (11): 975-985. Bibcode:1994AmJPh..62..975A. doi:10.1119/1.17656.
- ↑ Lodge, Oliver (1897). «Experiments on the Absence of Mechanical Connexion between Ether and Matter». Phil. Trans. Roy. Soc. 189: 149-166.
- ↑ Michelson, A.A. (1904). «Relative Motion of Earth and Aether». Philosophical Magazine 8 (48): 716-719.
- ↑ a b Pauli, Wolfgang (1981). Theory of Relativity. Nueva York: Dover. ISBN 0-486-64152-X.
- ↑ Laue, Max von (1911). «On an Experiment on the Optics of Moving Bodies». Münchener Sitzungsberichte: 405-412.
- ↑ Guido Rizzi, Matteo Luca Ruggiero (1981). «The relativistic Sagnac Effect: two derivations». En G. Rizzi and M.L. Ruggiero, ed. Relativity in Rotating Frames. Dordrecht: Kluwer Academic Publishers. ISBN 0-486-64152-X. arXiv:gr-qc/0305084.
- ↑ L.D. Landau, E.M. Lifshitz, (1962). “The Classical Theory of Fields”. 2nd edition, Pergamon Press, pp. 296 - 297.
- ↑ Sagnac, Georges (1913). «The demonstration of the luminiferous aether by an interferometer in uniform rotation». Comptes Rendus 157: 708-710.
- ↑ Sagnac, Georges (1913). «On the proof of the reality of the luminiferous aether by the experiment with a rotating interferometer». Comptes Rendus 157: 1410-1413.
- ↑ Laue, Max von (1920). «Zum Versuch von F. Harreß». Annalen der Physik 367 (13): 448-463. Bibcode:1920AnP...367..448L. doi:10.1002/andp.19203671303.
- ↑ Albert Abraham Michelson, Henry G. Gale: The Effect of the Earth's Rotation on the Velocity of Light, in: The Astrophysical Journal 61 (1925), S. 140–145
- ↑ Ruyong Wang, Yi Zheng, Aiping Yao, Dean Langley (2003). «Modified Sagnac Experiment for Measuring Travel-time Difference between Counter-propagating Light Beams in a Uniformly Moving Fiber». Physics Letters A 312: 7-10. Bibcode:2003PhLA..312....7W. arXiv:physics/0609222. doi:10.1016/S0375-9601(03)00575-9.
- ↑ Ruyong Wang, Yi Zheng, Aiping Yao (2004). «Generalized Sagnac Effect». Physical Review Letters 93 (14): 143901. Bibcode:2004PhRvL..93n3901W. arXiv:physics/0609235. doi:10.1103/PhysRevLett.93.143901.
- ↑ Hariharan, P. (1975). «Sagnac or Michelson-Sagnac interferometer?». Applied Optics 14 (10): 2319_1-2311. doi:10.1364/AO.14.2319_1.
- ↑ Michelson, A. A.; Morley, E.W. (1886). «Influence of Motion of the Medium on the Velocity of Light». Am. J. Science 31: 377-386.
- ↑ Hariharan, P. (2003). Optical Interferometry (Second edición). Academic Press. pp. 28–29. ISBN 0-12-311630-9.
- ↑ a b c Sun, K-X.; Fejer, M.M.; Gustafson, E.; Byer R.L. (1996). «Sagnac Interferometer for Gravitational-Wave Detection». Physical Review Letters 76 (17): 3053-3056. Bibcode:1996PhRvL..76.3053S. doi:10.1103/PhysRevLett.76.3053. Consultado el 31 de marzo de 2012.
- ↑ Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; Beveridge, N.; Birindelli, S.; Bose, S.; Bosi, L.; Braccini, S.; Bradaschia, C.; Bulik, T.; Calloni, E.; Cella, G.; Chassande Mottin, E.; Chelkowski, S.; Chincarini, A.; Clark, J.; Coccia, E.; Colacino, C.; Colas, J.; Cumming, A.; Cunningham, L.; Cuoco, E.; Danilishin, S. (2010). «The third generation of gravitational wave observatories and their science reach». Classical and Quantum Gravity 27 (8): 084007. Bibcode:2010CQGra..27h4007P. doi:10.1088/0264-9381/27/8/084007.
- ↑ Freise, A.; Chelkowski, S.; Hild, S.; Pozzo, W. D.; Perreca, A.; Vecchio, A. (2009). «Triple Michelson interferometer for a third-generation gravitational wave detector». Classical and Quantum Gravity 26 (8): 085012. Bibcode:2009CQGra..26h5012F. arXiv:0804.1036. doi:10.1088/0264-9381/26/8/085012.
- ↑ Eberle, T.; Steinlechner, S.; Bauchrowitz, J. R.; Händchen, V.; Vahlbruch, H.; Mehmet, M.; Müller-Ebhardt, H.; Schnabel, R. (2010). «Quantum Enhancement of the Zero-Area Sagnac Interferometer Topology for Gravitational Wave Detection». Physical Review Letters 104 (25). Bibcode:2010PhRvL.104y1102E. arXiv:1007.0574. doi:10.1103/PhysRevLett.104.251102.
Enlaces externos[editar]
- Giróscopos láser grande para el monitoreo de la rotación de la tierra Archivado el 1 de julio de 2009 en Wayback Machine. (en inglés)
- Artículo de MathPages sobre el efecto Sagnac (en inglés)
- Anillo láser, pruebas de física fundamental y Geofísica (en inglés, una extensa revisión de Stedman E G. PDF-file, 1,5 MB).
- El efecto Sagnac y su aplicación para GPS (en inglés, artículo GPS por Neil Ashby).
- Datos en vivo desde Nueva Zelanda de girocompás de anillo láser 21 m x 40 m (en inglés)




























