Tronco de cono

Tronco de cono.

Tronco de cono.

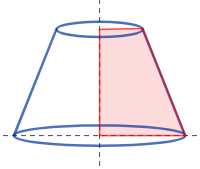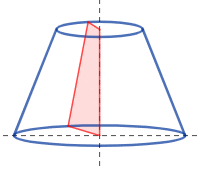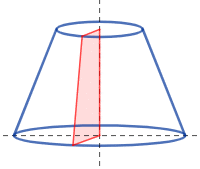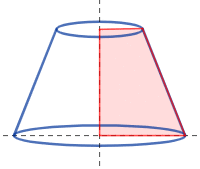
El tronco de cono,cono truncado o tronco de Garófalo es un volumen de revolución generado por un trapecio rectángulo al tomar como eje de giro el lado perpendicular a las bases.

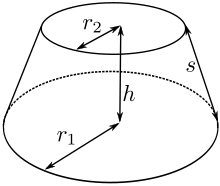
Un tronco de cono recto, de bases paralelas, es la porción de cono comprendido entre dos planos que lo cortan y son perpendiculares a su eje. Queda determinado por los radios de las bases, $r_1 \,$ y $r_2 \,$, la altura, $h \,$, y la generatriz, $s \,$, entre las cuales se cumple la relación del teorema de Pitágoras:

$s^2 = \left(r_1 - r_2 \right)^2 + h^2$

El área lateral de un tronco de cono se puede hallar mediante la semisuma de los perímetros de las bases, por la generatriz:

$A_L = \frac {2 \pi r_1 + 2 \pi r_2 }{2} s$

$A_L = \pi \left(r_1 + r_2 \right)s$

El área de un tronco de cono, la cuál es el área lateral más el área de las bases superior e inferior, se puede hallar mediante la fórmula:

$A = A_1 + A_2 + A_L \,$

$A = \pi r_1^2 + \pi r_2^2 + \pi \left(r_1 + r_2 \right) s$

$A = \pi \left[ r_1^2 + r_2^2 + (r_1 + r_2 \right) s ]$

El volumen de un tronco de cono se puede hallar utilizando el producto entre la altura del tronco y la media heroniana del área de las bases:

$V = \frac{h}{3} \left(A_1 + A_2 + \sqrt {A_1 A_2}\right) \,$

$V = \frac{h}{3} \left(\pi r_1^2 + \pi r_2^2 + \sqrt { \pi r_1^2 \pi r_2^2}\right) \,$

$V = \frac{h \pi}{3} (r_1^2 + r_2^2 + r_1 r_2) \,$

Véase también

• Tronco (geometría)
• Tronco de pirámide
• Media heroniana

Enlaces externos

• Weisstein, Eric W. «Tronco de cono» (en inglés). MathWorld. Wolfram Research.
• Derivation of formula for the volume of frustums of pyramid and cone (Mathalino.com)
• Problema práctico sobre el volumen de un tronco de cono elíptico