Conicidad

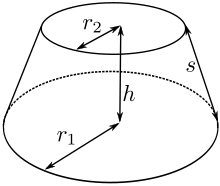
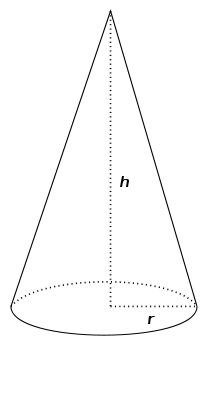
La conicidad es la relación que existe en un tronco de cono recto entre la diferencia de su diámetro mayor (base) menos el menor y su altura. De igual manera, en un cono —que es un caso particular de un tronco de cono cuya base menor tiene un diámetro nulo— la conicidad es la relación entre el diámetro de la base y la altura.

c={\frac {D_{1}-D_{2}}{h}}=2\cdot {\frac {r_{1}-r_{2}}{h}}

;

donde c es la conicidad; h es la altura del cono truncado; D₁ y D₂ son los diámetros mayor y menor del tronco de cono respectivamente; y r₁ y r₂ son los radios mayor y menor.

La conicidad se expresa, bien por unidad de longitud de la altura, bien en porcentaje, o en forma de fracción (1:x).

Conicidad e inclinación

La inclinación de un tronco de cono es la relación que existe entre el incremento de radio y la altura, por tanto es la mitad de la conicidad.

i={\frac {r_{1}-r_{2}}{h}}={\frac {c}{2}}

;

La inclinación también se expresa, bien por unidad de longitud de la altura, bien en porcentaje, o en forma de fracción (1:x).

Conicidad y ángulos

El ángulo α entre una generatriz de un cono y su eje de simetría se obtiene mediante la siguiente relación trigonométrica:

\tan \alpha ={\frac {r_{1}-r_{2}}{h}}={\frac {c}{2}}=i

\alpha =\arctan \left({\frac {r_{1}-r_{2}}{h}}\right)=\arctan \left({\frac {c}{2}}\right)=\arctan i

El ángulo β del vértice de un cono es el que forman dos generatrices opuestas entre sí y es igual al doble del ángulo entre una generatriz y el eje.

\beta =2\alpha =2\cdot \arctan \left({\frac {r_{1}-r_{2}}{h}}\right)=2\cdot \arctan \left({\frac {c}{2}}\right)=2\cdot \arctan i

Ejemplo

Sea un tronco de cono de 80 mm de altura, con un diámetro mayor de 100 mm y un diámetro menor de 84 mm.

Su conicidad será:

c={\frac {D_{1}-D_{2}}{h}}={\frac {100-84}{80}}={\frac {1}{5}}=0,2=20\%=1:5

Expresada en tanto por uno, la conicidad es de 0,2.
Expresada en tanto por ciento, la conicidad es de 20%.
Expresada en forma de fracción propia, la conicidad es de 1:5.

Su inclinación será:

i={\frac {r_{1}-r_{2}}{h}}={\frac {c}{2}}=0,1=10\%=1:10

El ángulo entre una generatriz y el eje de simetría será:

\alpha =\arctan \left({\frac {50-42}{80}}\right)=\arctan \left({\frac {1}{10}}\right)=\arctan i

α ≈ 5,710593° ≈ 5º 42' 38,14''.

El ángulo entre generatrices opuestas será el doble del anterior:

β = 2α ≈ 11,421186° ≈ 11º 25' 16,27''.

Referencias

Corbella Barrios, David (1970). «Elementos cónicos», en Elementos de normalización: dibujo técnico 3. Danubio, S. L. Artes Gráficas. Depósito legal: M-17669-1970. Pp. 148 y ss.
Millán Gómez, Simón (2006). «Verificación dimensional y geometría», en Procedimientos de mecanizado. Paraninfo. ISBN 978-84-9732-428-1. Pág. 243 y ss.

Datos: Q5783204