Sistema ortocéntrico
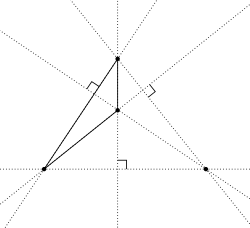
En geometría, un sistema ortocéntrico es un conjunto de cuatro puntos en un plano, cada uno de los cuales es el ortocentro del triángulo formado por los otros tres.
Si cuatro puntos forman un sistema ortocéntrico, entonces cada uno de los cuatro puntos es el ortocentro de los otros tres. Estos cuatro triángulos posibles tendrán la misma circunferencia de los nueve puntos. En consecuencia, estos cuatro triángulos posibles deben tener circunferencias circunscritas con el mismo circunradio.
Circunferencia de nueve puntos común[editar]

El centro de esta circunferencia común de nueve puntos se encuentra en el centroide de los cuatro puntos ortocéntricos. El radio de la circunferencia común de nueve puntos es la distancia desde el centro de nueve puntos al punto medio de cualquiera de los seis conectores que unen cualquier par de puntos ortocéntricos a través de los que pasa la circunferencia común de nueve puntos, que también pasa a través de las tres intersecciones ortogonales a los pies de las alturas de los cuatro triángulos posibles.
Este centro de la circunferencia común de nueve puntos se encuentra en el punto medio del conector que une cualquiera de los cuatro puntos del sistema ortocentrico al circuncentro del triángulo formado a partir de los otros tres.
La circunferencia común de nueve puntos es tangente a los 16 incírculos y excírculos de los cuatro triángulos cuyos vértices forman el sistema ortocéntrico.[1]
El triángulo órtico común, su incentro y excentros[editar]
Si los seis conectores que unen cualquier par de puntos ortocéntricos se extienden a seis líneas que se cruzan entre sí, generan siete puntos de intersección. Cuatro de estos puntos son los puntos ortocéntricos originales y los tres puntos adicionales son las intersecciones ortogonales a los pies de las alturas. La unión de estos tres puntos ortogonales en un triángulo genera un triángulo órtico que es común a todos los cuatro triángulos posibles formados a partir de los cuatro puntos del sistema ortocéntrico tomados de tres en tres.
Tengase en cuenta que el incentro de este triángulo órtico común debe ser uno de los cuatro puntos ortocéntricos originales. Además, los tres puntos restantes se convierten en los excentros de este triángulo órtico común. El punto ortocéntrico que se convierte en el incentro del triángulo órtico es ese punto ortocéntrico más cercano al centro común de nueve puntos. Esta relación entre el triángulo órtico y los cuatro puntos ortocéntricos originales conduce directamente al hecho de que el incentro y los excentros de un triángulo de referencia forman un sistema ortocéntrico.[2]: p.182
Es normal distinguir uno de los puntos ortocéntricos de los otros, específicamente el que es el incentro del triángulo órtico; este se denota H, como el ortocentro de los tres puntos ortogénicos externos que se eligen como un triángulo de referencia ABC. En esta configuración normalizada, el punto H siempre estará dentro del triángulo ABC y todos los ángulos del triángulo ABC serán agudos. Los cuatro triángulos posibles mencionados anteriormente son entonces los triángulos ABC, ABH, ACH y BCH. Los seis conectores mencionados anteriormente son AB, AC, BC, AH, BH y CH. Las siete intersecciones mencionadas anteriormente son A, B, C, H (los puntos ortocéntricos originales) y HA, HB, HC (los pies de las alturas del triángulo ABC y los vértices del triángulo órtico).
El sistema ortocéntrico y sus ejes órticos[editar]
El eje órtico asociado con un sistema ortogénico normalizado A, B, C y H, donde ABC es el triángulo de referencia, es una línea que pasa por tres puntos de intersección formados cuando cada lado del triángulo órtico se encuentra con cada lado del triángulo de referencia. Ahora considérense los otros tres triángulos posibles, ABH, ACH y BCH. Cada uno tiene su propio eje órtico.
Líneas de Euler y sistemas ortocéntricos homotéticos[editar]

Sean los vectores a, b, c y h que determinan la posición de cada uno de los cuatro puntos ortogénicos y sea n = (a + b + c + h) / 4 el vector de posición de N, el centro de la circunferencia común de nueve puntos. Únase cada uno de los cuatro puntos ortogénicos a su centro común de nueve puntos y extiéndasen en cuatro rectas. Estas cuatro líneas ahora representan las recras de Euler de los cuatro triángulos posibles, donde la línea extendida HN es la recta de Euler del triángulo ABC y la línea extendida AN es la recta de Euler del triángulo BCH etc. Si se elige un punto P en la recta de Euler HN del triángulo de referencia ABC con un vector de posición p tal que p = n + α (h − n) donde α es una constante pura independiente de la posición de los cuatro puntos ortogénicos, y tres puntos más, PA, PB, PC tales que pa = n + α (a & menos; n) etc., entonces P, PA, PB y PC forman un sistema ortocéntrico. Este sistema ortogénico generado es siempre homotético para el sistema original de cuatro puntos con el centro común de nueve puntos como centro homotético y α la relación de semejanza.
Cuando se elige como P el centroide G, entonces α = −1/3. Cuando P se elige como el circuncentro O, entonces α = −1 y el sistema ortogénico generado es congruente con el sistema original, además de ser un reflejo del centro de la circunferencia de nueve puntos. En esta configuración PA, PB, PC forman un triángulo de Johnson del triángulo de referencia original ABC. En consecuencia, los circuncentros de los cuatro triángulos ABC , ABH , ACH , BCH son todos iguales y forman un conjunto de círculos de Johnson, como se muestra en el diagrama adyacente.
Otras propiedades[editar]
Las cuatro rectas de Euler de un sistema ortocéntrico son ortogonales a los cuatro ejes órticos de un sistema ortocéntrico.
Los seis conectores que unen cualquier par de los cuatro puntos ortogénicos originales producirán pares de conectores que son ortogonales entre sí de forma que satisfacen las ecuaciones de distancia
donde R es el circunradio común de los cuatro triángulos posibles. Estas ecuaciones junto con el teorema de los senos dan como resultado la identidad
El teorema de Feuerbach establece que la circunferencia de nueve puntos es tangente al incírculo y a las tres excircunferencias de un triángulo de referencia. Debido a que la circunferencia de nueve puntos es común a los cuatro triángulos posibles en un sistema ortocéntrico, es tangente a 16 círculos que comprenden los incírculos y los excírculos de los cuatro triángulos posibles.
Cualquier cónica que pase por los cuatro puntos ortogénicos solo puede ser una hipérbola equilátera. Esto es un resultado del teorema cónico de Feuerbach, que establece que para todas las circuncónicas de un triángulo de referencia que también pasan a través de su ortocentro, el Lugar geométrico del centro de tales circuncónicas forman el círculo de nueve puntos y que la circuncónicas solo pueden ser hipérbolas equiláteras.
Téngase en cuenta que el lugar geométrico de los perspectores de esta familia de hipérbolas equiláteras siempre estará en los cuatro ejes órticos. Entonces, si una hipérbola equilátera pasa a través de cuatro puntos ortogénicos, tendrá un centro fijo en la circunferencia común de nueve puntos, pero tendrá cuatro perspectores, uno en cada uno de los ejes órticos de los cuatro triángulos posibles. Téngase en cuenta también que el único punto en la circunferencia de nueve puntos (que es el centro de esta hipérbola equilátera) tendrá cuatro definiciones diferentes dependiendo de cuál de los cuatro triángulos posibles se utiliza como el triángulo de referencia.
Las hipérbolas equiláteras bien documentadas que pasan por cuatro puntos ortogénicos son las circunhipérbolas de Feuerbach, Jeřábek y Kiepert del triángulo de referencia ABC en un sistema normalizado con H como ortocentro.
Los cuatro triángulos posibles tienen un conjunto de cuatro incónicas conocidas como las incónicas órticas que comparten ciertas propiedades. Las tangencias de estas incónicas con los cuatro triángulos posibles se producen en los vértices de su triángulo órtico común. En un sistema ortocéntrico normalizado, la incónica órtica que es tangente a los lados del triángulo ABC es un inelipse y las incónicas órticas de los otros tres triángulos posibles son hipérbolas. Estos cuatro puntos críticos también comparten el mismo punto de Brianchon, H, el punto ortocéntrico más cercano al centro común de la circunferencia de nueve puntos. Los centros de estas incónicas órticas son los puntos simedianos K de los cuatro triángulos posibles.
Hay muchas curvas cúbicas documentadas que pasan por un triángulo de referencia y su ortocentro. La circuncúbica conocida como ortocúbica - K006 es interesante porque pasa a través de los tres sistemas ortocéntricos, así como por los tres vértices del triángulo órtico (pero no por el ortocentro del triángulo órtico). Los tres sistemas ortogénicos son el incentro y el excentro, el triángulo de referencia y su ortocentro y finalmente el ortocentro del triángulo de referencia junto con los otros tres puntos de intersección que esta cúbica tiene con la circunferencia circunscrita del triángulo de referencia.
Dos circunferencias polares de dos triángulos en un sistema ortocéntrico son ortogonales.[2]: p. 177
Referencias[editar]
Enlaces externos[editar]
- Weisstein, Eric W. «Orthocenter». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Feuerbach's Theorem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Feuerbach's Conic Theorem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Feuerbach Hyperbola». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Jerabek Hyperbola». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Kiepert Hyperbola». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Orthic Inconic». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Orthic Axis». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Perspector». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Bernard Gibert Circumcubic K006
- Clark Kimberling, "Encyclopedia of Triangle Centers". (Enumera unos 5000 puntos interesantes asociados con cualquier triángulo)


