Onda


En física, una onda (del latín unda) consiste en la propagación de una fluctuación o perturbación en alguna propiedad del espacio, por ejemplo, densidad, presión, campo eléctrico o campo magnético, implicando un transporte de energía sin transporte de materia. El espacio perturbado puede contener materia (aire, agua, etc.) o no (vacío).
La magnitud física cuya perturbación se propaga en el medio se expresa como una función tanto de la posición como del tiempo . Matemáticamente se dice que dicha función es una onda si verifica la ecuación de ondas:
donde es la velocidad de propagación de la perturbación. Por ejemplo, ciertas perturbaciones de la presión de un medio, llamadas sonido, verifican la ecuación anterior, aunque algunas ecuaciones no lineales también tienen soluciones ondulatorias, por ejemplo, un solitón.
Definición[editar]
Una vibración puede no tener las características necesarias y suficientes que definen a una onda. El término suele ser entendido intuitivamente como el transporte de vibraciones en el espacio, o medio en el que pueden producirse y propagarse dichas perturbaciones, al variar alguna de sus propiedades medibles.
La teoría de ondas se conforma como una característica rama de la física que se ocupa de las propiedades de los fenómenos ondulatorios independientemente de cuál sea su origen físico (Ostrovsky y Potapov, 1999). Una peculiaridad de estos fenómenos ondulatorios es que a pesar de que el estudio de sus características no depende del tipo de onda en cuestión, los distintos orígenes físicos que provocan su aparición les confieren propiedades muy particulares que distinguen a unos fenómenos de otros. Por ejemplo, la acústica se diferencia de la óptica en que las ondas sonoras están relacionadas con aspectos más mecánicos que las ondas electromagnéticas (que son las que gobiernan los fenómenos ópticos). Conceptos tales como masa, cantidad de movimiento, inercia o elasticidad son conceptos importantes para describir procesos de ondas sonoras, a diferencia de las ópticas, donde estas no tienen una especial relevancia. Por lo tanto, las diferencias en el origen o naturaleza de las ondas producen ciertas propiedades que caracterizan cada onda, manifestando distintos efectos en el medio en que se propagan (por ejemplo, en el caso del aire: vórtices, ondas de choque; en el caso de los sólidos: dispersión; y en el caso del electromagnetismo presión de radiación).
Componentes de una onda[editar]
- Elongación (): Es la distancia que hay, en forma perpendicular, entre un punto de la onda y la línea de equilibrio.
- Cresta: Es el punto de máxima elongación de la onda; es decir, el punto de la onda más separado de su posición de reposo.
- Valle: Es el punto de mínima elongación de la onda, en sentido opuesto a la cresta.
- Nodo: Es el punto donde la onda cruza la línea de equilibrio.
- Ciclo: Es una oscilación, o el recorrido desde el nodo que inicia la trayectoria de la cresta hasta el nodo que termina la trayectoria del valle o viceversa.
- Amplitud (): Es la distancia vertical entre una cresta o valle y el punto de equilibrio de la onda. Nótese que pueden existir ondas cuya amplitud sea variable, es decir, crezca o decrezca con el paso del tiempo.
- Longitud de onda (): Es la distancia que hay entre el mismo punto de dos ondulaciones consecutivas, o la distancia entre dos crestas, valles o tres nodos consecutivos.
- Periodo (): Es el tiempo empleado en completar una longitud de onda (oscilación completa).
- Frecuencia (): Es el número de periodos por unidad de tiempo. Es decir: el número de veces que es repetida dicha vibración por unidad de tiempo.
- Fase (Φ): La fase indica la situación instantánea en el ciclo, de una magnitud que varía cíclicamente, siendo la fracción del periodo transcurrido desde el instante correspondiente al estado tomado como referencia.
- Velocidad de propagación: Es la velocidad a la que se propaga el movimiento ondulatorio. Su valor es el cociente de la longitud de onda y su período.
- línea de equilibrio:
Características[editar]

B = En aguas superficiales. El movimiento elíptico de una partícula superficial se vuelve suave con la baja intensidad.
1 = Progresión de la onda
2 = Monte
3 = Valle
Las ondas periódicas están caracterizadas por cruzar montes y valles, y usualmente es categorizada como longitudinal o transversal. Una onda transversal es aquella con las vibraciones perpendiculares a la dirección de propagación de la onda; ejemplos incluyen ondas en una cuerda y ondas electromagnéticas. Onda longitudinal es aquella con vibraciones paralelas en la dirección de la propagación de las ondas; ejemplos incluyen ondas sonoras.
Cuando un objeto corta hacia arriba y abajo en una onda en un estanque, experimenta una trayectoria orbital porque las ondas no son simples ondas transversales sinusoidales.
Ondas en la superficie de una cuba son realmente una combinación de ondas transversales y longitudinales; por lo tanto, los puntos en la superficie siguen caminos orbitales.
Todas las ondas tienen un comportamiento común bajo un número de situaciones estándar. Todas las ondas pueden experimentar los siguientes fenómenos:
- Difracción: Ocurre cuando una onda al topar con el borde de un obstáculo deja de ir en línea recta para rodearlo.
- Efecto Doppler: Efecto debido al movimiento relativo entre la fuente emisora de las ondas y el receptor de las mismas.
- Interferencia: Ocurre cuando dos ondas se combinan al encontrarse en el mismo punto del espacio.
- Reflexión: Ocurre cuando una onda, al encontrarse con un nuevo medio que no puede atravesar, cambia de dirección.
- Refracción: Ocurre cuando una onda cambia de dirección al entrar en un nuevo medio en el que viaja a distinta velocidad.
- Onda de choque: Ocurre cuando varias ondas que viajan en un medio se superponen formando un cono.
Polarización[editar]

Una onda es polarizada, si solo puede oscilar en una dirección. La polarización de una onda transversal describe la dirección de la oscilación, en el plano perpendicular a la dirección del viaje. Ondas longitudinales tales como ondas sonoras no exhiben polarización, porque para estas ondas la dirección de oscilación es a lo largo de la dirección de viaje. Una onda transversal, como la luz puede ser polarizada usando un filtro polarizador o al ser reflejada por un dieléctrico inclinado, ej. vidrio de ventana.
Ejemplos[editar]
Ejemplos de ondas:
- Olas, que son perturbaciones que se propagan por el agua.
- Ondas de radio, microondas, ondas infrarrojas, luz visible, luz ultravioleta, rayos X, y rayos gamma conforman la radiación electromagnética. En este caso, la propagación es posible sin un medio, a través del vacío. Las ondas electromagnéticas viajan a 299 792 458 m/s en el vacío.
- Sonoras — una onda mecánica que se propaga por el aire, los líquidos o los sólidos.
- Ondas de tráfico (esto es, la propagación de diferentes densidades de vehículos, etc.) — estas pueden modelarse como ondas cinemáticas como hizo Sir M. J. Lighthill
- Ondas sísmicas en terremotos.
- Ondas gravitacionales, que son fluctuaciones en la curvatura del espacio-tiempo predichas por la relatividad general. El 17 de marzo de 2014 se anunció la observación experimental de los restos de ondas gravitacionales durante el periodo de expansión del universo tras el Big Bang, pero el descubrimiento se puso en entredicho posteriormente.[1]
Descripción matemática[editar]


Desde un punto de vista matemático, la onda más sencilla o fundamental es la onda sinusoidal descrita por la función
donde es la amplitud de una onda (la elongación máxima o altura de la cresta de la onda). Las unidades de amplitud dependen del tipo de onda — las ondas en una cuerda tienen una amplitud expresada como una distancia (metros), las ondas sonoras como presión (pascales) y ondas electromagnéticas como la amplitud del campo eléctrico (voltios/metros). La amplitud puede ser constante, o puede variar con el tiempo y/o posición. La forma de la variación de amplitud es llamada la envolvente de la onda.
La longitud de onda (simbolizada por ) es la distancia entre dos crestas o valles seguidos. Se mide en unidades de longitud, tales como el metro(m), sus múltiplo o submúltiplos según convenga. Así, en la óptica, la longitud de onda de la luz se mide en nanómetros.
Un número de onda angular puede ser asociado con la longitud de onda por la relación:

El periodo es el tiempo requerido para que el movimiento de oscilación de la onda describa un ciclo completo. La frecuencia es el número de ciclos completos transcurridos en la unidad de tiempo (por ejemplo, un segundo). Es medida en hercios. Matemáticamente se define sin ambigüedad como:
En otras palabras, la frecuencia y el periodo de una onda son recíprocas entre sí.
La frecuencia angular representa la frecuencia en radianes por segundo. Está relacionada con la frecuencia por
Hay dos velocidades diferentes asociadas a las ondas. La primera es la velocidad de fase o velocidad de propagación, la cual indica la tasa con la que la onda se propaga, y está dada por:
La segunda es la velocidad de grupo, la cual da la velocidad con la que las variaciones en la forma de la amplitud de la onda se propagan por el espacio. Esta es la tasa a la cual la información puede ser transmitida por la onda. Está dada por:
Ecuación de onda[editar]
La ecuación de onda es un tipo de ecuación diferencial que describe la evolución de una onda armónica simple a lo largo del tiempo. Esta ecuación presenta ligeras variantes dependiendo de cómo se transmite la onda, y del medio a través del cual se propaga. Si consideramos una onda unidimensional que se transmite a lo largo de una cuerda en el eje x, a una velocidad y con una amplitud (que generalmente depende tanto de y de ), la ecuación de onda es:
Trasladado a tres dimensiones, sería
donde es el operador laplaciano.
La velocidad depende del tipo de onda y del medio a través del cual viaja.
Jean le Rond d'Alembert obtuvo una solución general para la ecuación de onda en una dimensión:
Esta solución puede interpretarse como dos impulsos viajando a lo largo del eje x en direcciones opuestas: F en el sentido +x y G en el -x. Si generalizamos la variable x, reemplazándola por tres variables x, y, z, entonces podemos describir la propagación de una onda en tres dimensiones.
La ecuación de Schrödinger describe el comportamiento ondulatorio de las partículas elementales. Las soluciones de esta ecuación son funciones de ondas que pueden emplearse para hallar la densidad de probabilidad de una partícula.
Onda simple[editar]
Es una perturbación que varía tanto con el tiempo como con la distancia de la siguiente manera:
donde es la amplitud de la onda, es el número de onda y es la fase. La velocidad de fase vf de esta onda está dada por
donde es la longitud de onda.
Onda estacionaria[editar]
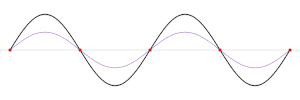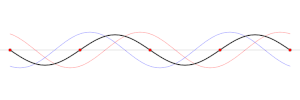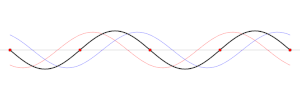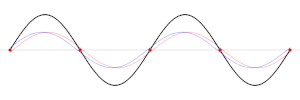
Una onda estacionaria es aquella que permanece fija, sin propagarse a través del medio. Este fenómeno puede darse, bien cuando el medio se mueve en sentido opuesto al de propagación de la onda, o bien puede aparecer en un medio estático como resultado de la interferencia entre dos ondas que viajan en sentidos opuestos.
La suma de dos ondas que se propagan en sentidos opuestos, con idéntica amplitud y frecuencia, dan lugar a una onda estacionaria. Las ondas estacionarias normalmente aparecen cuando una frontera bloquea la propagación de una onda viajera (como los extremos de una cuerda, o el bordillo de una piscina, más allá de los cuales la onda no puede propagarse). Esto provoca que la onda sea reflejada en sentido opuesto e interfiera con la onda inicial, dando lugar a una onda estacionaria. Por ejemplo, cuando se rasga la cuerda de un violín, se generan ondas transversales que se propagan en direcciones opuestas por toda la cuerda hasta llegar a los extremos. Una vez aquí son reflejadas de vuelta hasta que interfieren la una con la otra dando lugar a una onda estacionaria, que es lo que produce su sonido característico.
Las ondas estacionarias se caracterizan por presentar regiones donde la amplitud es nula (nodos) y otras donde es máxima (vientres). La distancia entre dos nodos o vientres consecutivos es justamente , donde es la longitud de onda de la onda estacionaria.
Al contrario que en las ondas viajeras, en las ondas estacionarias no se produce propagación de energía.
Para calcular la velocidad de onda estacionaria se aplica la fórmula:
- donde
donde
es la amplitud de la onda de cada punto del medio y es la pulsación en cada punto del medio.
Como la amplitud de la onda depende de tendremos que se anulará cuando para
Por lo tanto, como el número de onda , sustituyendo tendremos que
- , por lo que para
Propagación en cuerdas[editar]
La velocidad de una onda viajando a través de una cuerda en vibración (v) es directamente proporcional a la raíz cuadrada de la tensión de la cuerda (T) por su densidad lineal (μ):
Clasificación de las ondas[editar]
Las ondas se clasifican siguiendo los diferentes aspectos:
En función del medio en el que se propagan[editar]

- Ondas mecánicas: las ondas mecánicas necesitan un medio elástico (sólido, líquido o gaseoso) para propagarse. Las partículas del medio oscilan alrededor de un punto fijo, por lo que no existe transporte neto de materia a través del medio. Como en el caso de una alfombra o un látigo cuyo extremo se sacude, la alfombra no se desplaza, sin embargo, una onda se propaga a través de ella. La velocidad puede ser afectada por algunas características del medio como: la homogeneidad, la elasticidad, la densidad y la temperatura. Dentro de las ondas mecánicas tenemos las ondas elásticas, las ondas sonoras y las ondas de gravedad.
- Ondas electromagnéticas: las ondas electromagnéticas se propagan por el espacio sin necesidad de un medio, por lo tanto pueden propagarse en el vacío. Esto se debe a que las ondas electromagnéticas son producidas por las oscilaciones de un campo eléctrico, en relación con un campo magnético asociado. Las ondas electromagnéticas viajan aproximadamente a una velocidad de 300 000 km por segundo, de acuerdo a la velocidad puede ser agrupado en rango de frecuencia. Este ordenamiento es conocido como Espectro Electromagnético, objeto que mide la frecuencia de las ondas.
- Ondas gravitacionales: las ondas gravitacionales son perturbaciones que alteran la geometría misma del espacio-tiempo y aunque es común representarlas viajando en el vacío, técnicamente no podemos afirmar que se desplacen por ningún espacio, sino que en sí mismas son alteraciones del espacio-tiempo.
En función de su dirección[editar]
- Ondas unidimensionales: las ondas unidimensionales son aquellas que se propagan a lo largo de una sola dimensión del espacio, como las ondas en los muelles o en las cuerdas. Si la onda se propaga en una dirección única, sus frentes de onda son planos y paralelos.
- Ondas bidimensionales o superficiales: son ondas que se propagan en dos dimensiones. Pueden propagarse, en cualquiera de las direcciones de una superficie, por ello, se denominan también ondas superficiales. Un ejemplo son las ondas que se producen en una superficie líquida en reposo cuando, por ejemplo, se deja caer una piedra en ella.
- Ondas tridimensionales o esféricas: son ondas que se propagan en tres dimensiones. Las ondas tridimensionales se conocen también como ondas esféricas, porque sus frentes de ondas son esferas concéntricas que salen de la fuente de perturbación expandiéndose en todas direcciones. Son ondas tridimensionales las ondas sonoras (mecánicas) y las ondas electromagnéticas.
En función del movimiento de sus partículas[editar]
- Ondas longitudinales: son aquellas que se caracterizan porque las partículas del medio se mueven o vibran paralelamente a la dirección de propagación de la onda. Por ejemplo, un muelle que se comprime da lugar a una onda longitudinal.
- Ondas transversales: son aquellas que se caracterizan porque las partículas del medio se mueven o vibran perpendicularmente a la dirección de propagación de la onda. Por ejemplo, las olas en el agua o las ondulaciones que se propagan por una cuerda.
En función de su periodicidad[editar]
- Ondas periódicas: la perturbación local que las origina se produce en ciclos repetitivos por ejemplo una onda senoidal.
- Ondas aperiódicas: Son las ondas en la que no se repite el mismo perfil de un ciclo a lo largo del tiempo. En las ondas aperiódicas existen componentes de todas las frecuencias.
Propiedades de las Ondas[editar]
Reflexión[editar]
Se produce cuando una onda encuentra en su recorrido una superficie contra la cual rebota, después de la reflexión la onda sigue propagándose en el mismo medio y los parámetros permanecen inalterados. El eco es un ejemplo de Reflexión.
Refracción[editar]
Es el cambio de dirección que experimenta una onda al pasar de un medio material a otro. Solo se produce si la onda incide oblicuamente sobre la superficie de separación de los dos medios y si estos tienen índices de refracción distintos. La refracción se origina en el cambio de velocidad que experimenta la onda. El índice de refracción es precisamente la relación entre la velocidad de la onda en un medio de referencia (el vacío para las ondas electromagnéticas) y su velocidad en el medio de que se trate.
Difracción[editar]
La difracción se produce cuando una onda llega a una ranura o un obstáculo de tamaño comparable con su longitud de onda. La onda se desvía como si el obstáculo emitiese una onda esférica.
Interferencia[editar]
Cuando en una región del espacio inciden dos o más ondas, los desplazamientos que producen sobre una partícula del medio se suman algebraicamente. Esto se llama interferencia.
Véase también[editar]
Referencias[editar]
- ↑ Ron Cowen (29 de mayo de 2014). «No evidence for or against gravitational waves». Nature (en inglés).
Bibliografía[editar]
- Campbell, M. and Greated, C. (1987). The Musician’s Guide to Acoustics. New York: Schirmer Books.
- French, A.P. (1971). Vibrations and Waves (M.I.T. Introductory physics series). Nelson Thornes. ISBN 0-393-09936-9.
- Hall, D. E. (1980). Musical Acoustics: An Introduction. Belmont, California: Wadsworth Publishing Company.
- Hunt, F. V. (1978). Origins in Acoustics. New York: Acoustical Society of America Press, (1992).
- Ostrovsky, L. A. and Potapov, A. S. (1999). Modulated Waves, Theory and Applications. Baltimore: The Johns Hopkins University Press.
- Vassilakis, P.N. (2001). Perceptual and Physical Properties of Amplitude Fluctuation and their Musical Significance. Doctoral Dissertation. University of California, Los Angeles.
Enlaces externos[editar]
 Wikimedia Commons alberga una galería multimedia sobre Onda.
Wikimedia Commons alberga una galería multimedia sobre Onda. Wikcionario tiene definiciones y otra información sobre onda.
Wikcionario tiene definiciones y otra información sobre onda.
- El Diccionario de la Real Academia Española tiene una definición para onda.





































