Integración indefinida

En cálculo infinitesimal, la función primitiva o antiderivada de una función f es una función F cuya derivada es f, es decir, F ′ = f.
Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua en dicho intervalo.
Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F1 y F2 son dos primitivas de f, entonces existe un número real C, tal que F1 = F2 + C. A C se le conoce como constante de integración. Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se representa como:
- o bien
El proceso de hallar la primitiva de una función se conoce como integración indefinida y es por tanto el inverso de la derivación. Las integrales indefinidas están relacionadas con las integrales definidas a través del teorema fundamental del cálculo, y proporcionan un método sencillo de calcular integrales definidas de numerosas funciones.
Ejemplo[editar]
Una primitiva de la función en es la función ya que:
Dado que la derivada de una constante es cero, tendremos que cos(x) tendrá un número infinito de primitivas tales como sin(x), sin(x) + 5, sin(x) - 100, etc. Es más, cualquier primitiva de la función f(x) = cos(x) será de la forma sin(x) + C donde C es una constante conocida como constante de integración.
Constante de integración[editar]
La derivada de cualquier función constante es cero. Una vez que se ha encontrado una primitiva F, si se le suma o resta una constante C, se obtiene otra primitiva. Esto ocurre porque (F + C) ' = F ' + C ' = F ' + 0 = F '. La constante es una manera de expresar que cada función tiene un número infinito de primitivas diferentes.
Para interpretar el significado de la constante de integración se puede observar el ñ de que la función f (x) es la derivada de otra función F (x), es decir, que para cada valor de x, f (x) le asigna la pendiente de F (x). Si se dibuja en cada punto (x, y) del plano cartesiano un pequeño segmento con pendiente f (x), se obtiene un campo vectorial como el que se representa en la figura de la derecha. Entonces el problema de encontrar una función F (x) tal que su derivada sea la función f (x) se convierte en el problema de encontrar una función de la gráfica de la cual, en todos los puntos sea tangente a los vectores del campo. En la figura de la derecha se observa como al variar la constante de integración se obtienen diversas funciones que cumplen esta condición y son traslaciones verticales unas de otras.
Otras propiedades[editar]
Linealidad de la integral indefinida[editar]
La primitiva es lineal, es decir:
- Si f es una función que admite una primitiva F sobre un intervalo I, entonces para todo real k, una primitiva de kf sobre el intervalo I es kF.
- Si F y G son primitivas respectivas de dos funciones f y g, entonces una primitiva de f + g es F + G.
La linealidad se puede expresar como sigue:
La primitiva de una función impar es siempre par[editar]
En efecto, como se ve en la figura siguiente, las áreas antes y después de cero son opuestas, lo que implica que la integral entre -a y a es nula, lo que se escribe así: F(a) - F(-a) = 0, F siendo una primitiva de f, impar. Por lo tanto siempre tenemos F(-a) = F(a): F es par.

La primitiva F de una función f par es impar con tal de imponerse F(0) = 0[1][editar]
En efecto, según la figura, las áreas antes y después de cero son iguales, lo que se escribe con la siguiente igualdad de integrales:

Es decir F(0) - F(-a) = F(a) - F(0). Si F(0) = 0, F(-a) = - F(a): F es impar.
La primitiva de una función periódica es la suma de una función lineal y de una función periódica[editar]
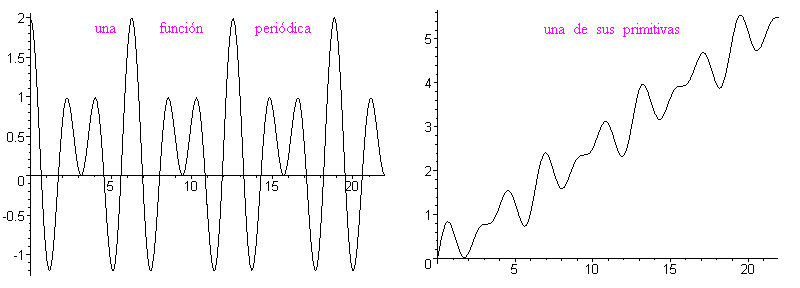
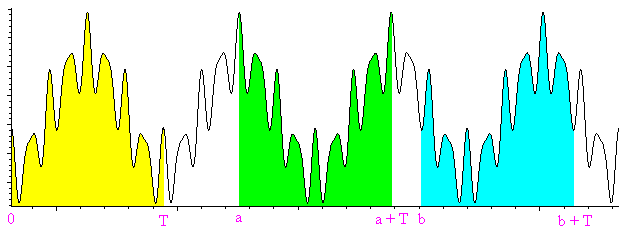
Para probarlo, hay que constatar que el área bajo una curva de una función periódica, entre las abcisas x y x + T (T es el período) es constante es decir no depende de x. La figura siguiente muestra tres áreas iguales. Se puede mostrar utilizando la periodicidad y la relación de Chasles, o sencillamente ¡con unas tijeras! (cortando y superponiendo las áreas de color).
En término de primitiva, significa que F(x + T) - F(x) es una constante, que se puede llamar A. Entonces la función G(x) = F(x) - Ax/T es periódica de período T. En efecto G(x + T) = F(x + T) - A(x + T)/T = F(x) + A - Ax/T - AT/T = F(x) - Ax/T = G(x). Por consiguiente F(x) = G(x) + Ax/T es la suma de G, periódica, y de Ax/T, lineal.
Relación entre la integral de una función y la de su inversa[editar]
Para simplificar, se impone f(0) = 0; a es un número cualquiera del dominio de f. Entonces tenemos la relación:

El área morada es la integral de f, el área amarilla es la de f -1, y la suma es el rectángulo cuyos costados miden a y f(a) (valores algebraicos). Se pasa de la primera curva, la de f, a la segunda, la de f -1 aplicando la simetría axial alrededor de la diagonal y = x.
El interés de esta fórmula es permitir el cálculo de la integral de f -1 sin conocer una primitiva; de hecho, ni hace falta conocer la expresión de la Función inversa.
Existencia de primitivas[editar]
Cualquier función continua sobre admite localmente una antiderivada o primitiva. Sin embargo en espacios de dimensión finita la continuidad no garantiza la existencia de antiderivadas. Una condición suficiente de existencia de antiderivadas es que la imagen pertenezca a un espacio vectorial conveniente, también llamado -completo. La propiedad definitoria de dichos espacios es que toda función con admite una función primitiva. Si el espacio no es -completo la continuidad o incluso la suavidad de una función no garantiza la existencia de antiderivadas.
Cálculo de primitivas[editar]
Integrales inmediatas[editar]
Para encontrar una primitiva de una función dada, basta con descomponerla (escribirla bajo forma de una combinación lineal) en funciones elementales cuyas primitivas son conocidas o se pueden obtener leyendo al revés una tabla de derivadas, y luego aplicar la linealidad de la integral:
Aquí están las principales funciones primitivas:
| Función : primitiva de | función : derivada de |
|---|---|
Por ejemplo, busquemos una primitiva de x → x(2-3x). Como no se conocen primitivas de un producto, desarrollemos la expresión: x(2-3x)= 2x - 3x2. 2x es la derivada de x2, 3x2 es la de x3, por lo tanto 2x - 3x2 tiene como primitiva x2 - x3 + k. Si además se pide que la primitiva verifique una condición F(x0) = y0 (que recibe el nombre de condición inicial cuando se trata de un problema de física), entonces la constante k es unívocamente determinada. En el ejemplo, si se impone F(2) = 3, entonces forzosamente k = 7.
Métodos de integración[editar]
Tenemos varios métodos a nuestra disposición:
- La linealidad de la integración nos permite descomponer integrales complicadas en otras más sencillas.
- Integración por sustitución, a menudo combinada con identidades trigonométricas o el logaritmo neperiano.
- Integración por partes para integrar productos de funciones.
- El método de la regla de la cadena inversa, un caso especial de la integración por sustitución.
- El método de fracciones parciales nos permite integrar todas las funciones racionales (fracciones de dos polinomios).
- El algoritmo de Risch.
- Integrales también pueden calcularse utilizando tablas de integrales.
Véase también[editar]
Referencias[editar]
- ↑ Stewart, James (1999). Cálculo de una variable. Trascendentes Tempranas (4ta edición). Thomson Learning. p. 415. ISBN 0-534-35563-3.
Enlaces externos[editar]
- Hazewinkel, Michiel, ed. (2001), «Indefinite_integral&oldid=11527», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104.
- Weisstein, Eric W. «Indefinite Integral». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Formulario de integrales







































