Función polinómica de grado 0
De Wikipedia, la enciclopedia libre
(Redirigido desde Función constante)
Se llama función polinómica de grado cero o función constante a la que no depende de ninguna variable, y la podemos representar como una función matemática de la forma:
donde a es la constante.
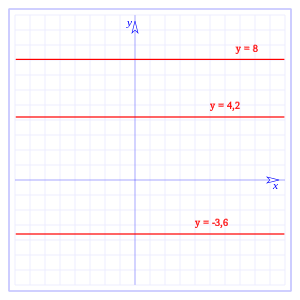
Como se puede ver es una recta horizontal en el plano xy, en la gráfica la hemos representado en el plano, pero, como se puede ver la función no depende de x, si hacemos:
tenemos:
donde a tiene un valor constante, en la gráfica tenemos representadas:
Como la variable dependiente y no depende de x tenemos que:
la variación de y respecto a x es cero
[editar] La función constante como un polinomio en x
Si un polinomio general, tiene la forma:
una función constante cumple esta expresión con n= 0, es un polinomio de grado 0.
que es lo mismo que:
que corresponde al termino independiente del polinomio.
