Sucesión (matemática)

En terminología matemática se incluye sucesión para designar la existencia de elementos encadenados o sucesivos.

Se excluye totalmente la sinonimia con el término serie.

En textos académicos se suele llamar simplemente sucesión con el bien entendido que todas son del mismo tipo. Esto no impide la existencia de sucesiones de diversas entidades matemáticas.

Cuando abundan sucesiones de todo tipo se puede cambiar incluso el nombre de sucesión por otro.

Véase secuencia, colección, familia y conjuntos en matemáticas.

Definiciones

Definición abstracta

Clase de finitos o numerables objetos ordenados.

Definición conjuntista

Una sucesión en un conjunto X es una enumeración de elementos de X, es decir una aplicación de $\mathbb {N}$ en X.

Notación

Notaremos por $\left\{{x_{n}}\right\}_{n\epsilon \mathbb {N} }$ a una sucesión, donde x la identifica como distinta de otra digamos $\left\{{y_{n}}\right\}_{n\epsilon \mathbb {N} }$.

La notación es permisiva en cuanto a su modificación si realmente es necesario.

Definición de término general

Llamaremos término general de una sucesión a $x_{n}^{}$,donde ${n\epsilon \mathbb {N} }$ indica el lugar que ocupa en dicha sucesión

Definición de parcial

Llamaremos parcial de $\left\{{x_{n}}\right\}_{n\epsilon \mathbb {N} }$ a una sucesión $\left\{{x_{n_{i}}}\right\}_{n_{i}\epsilon \mathbb {N} }$ donde $n_{i}^{}<n_{i+1}^{}$

Ejemplos en distintas áreas

Estos ejemplos pretenden ser una pequeña muestra de la infinidad, propiamente dicha, de usos que tienen dichas sucesiones en matemáticas.

El trabajo interno en el desarrollo de cada tema en cada área obliga a diversificar el modo de nominar y notar las sucesiones, haciéndose frecuente el uso de índices, subíndices y superíndices para salvar la sobrecarga de notación y hacerlas más legibles y estéticas en cuanto a la presentación.

En $\mathbb {C} ^{n}$

Se puede tener una sucesión $\left\{{V^{(i)}}\right\}_{i\epsilon \mathbb {N} }$ tal que ${V^{(i)}}{:=(a_{1}^{(i)},...,a_{n}^{(i)}),donde\;a_{j}^{(i)}}\in \mathbb {C}$

En el espacio de las sucesiones finitas en $\mathbb {C}$

Se puede tener una sucesión $\left\{{a^{(i)}}\right\}_{i\epsilon \mathbb {N} }$ tal que ${a^{(i)}}{:=(a_{1}^{(i)},...,a_{n_{i}}^{(i)},0,...),donde\;a_{j}^{(i)}}\in \mathbb {C} -\left\{0\right\}$

En K[x]

Un polinómio $P(x)\in K[x]$ no es más que una sucesión finita $\left\{{a_{n}}\right\}_{n}$ tal que $a_{n}\in K$ representada como $P(x)_{}^{}=a_{0}+a_{1}x+a_{2}x^{2}+...+a_{n}x^{n}$.

En $M_{m\times n}(k)$

Se puede tener una sucesión $\left\{{A_{i}}\right\}_{i\in \mathbb {N} }$ tal que $A_{i}:={\begin{pmatrix}a_{1,1}^{(i)}&\ldots &a_{1,n}^{(i)}\\\vdots &&\vdots \\a_{m,1}^{(i)}&\ldots &a_{m,n}^{(i)}\end{pmatrix}}$, donde $a_{j,k}^{(i)}\in K$.

En un espacio vectorial topológico

Se puede tener una sucesión $\left\{{V_{i}^{}}\right\}_{i\epsilon \mathbb {N} }$, donde $V_{n}^{}:=\alpha _{n}B$, donde $\alpha _{n}\in \mathbb {R}$ es una sucesión real arbitraria y B un abierto.

Sucesiones funcionales

Se puede tener una sucesión de funciones continuas $\left\{{{f(x)}_{n}}\right\}_{n\epsilon \mathbb {N} }=sin(x)^{n}$.

En el lenguaje proposicional

Sea $A_{}^{}$ un alfabeto, llamaremos $A_{}^{n}$ al conjunto de sucesiones finitas de n elementos de $A$, se define inductivamente por la sucesión de productos cartesianos siguiente: $A^{1}=A,A^{2}=A\times A,...,A^{n}:=A^{n-1}\times A$

• así ${<}a_{1},...,a_{n}>:={<<}a_{1},...,a_{n-1}{>},a_{n}{>}\in A^{n}{,y\;}a_{i}:={<}a_{i}{>}\in A$.

En homología simplicial

El complejo de cadenas simplicial del complejo simplicial K, no es más que una determinada sucesión de grupos abelianos y morfismos

En el lenguaje de las categorías

Sea ${\mathcal {A}}$ una categoría, podemos tener una sucesión $\left\{{A_{n}}\right\}_{n\in \mathbb {N} }$, donde $A_{n}^{}\in Ob({\mathcal {A}})$.

Sucesiones numéricas

Habitualmente presentada como una aplicación de los naturales en los reales

${\begin{matrix}u:&\mathbb {N} &\to &\mathbb {R} \\&n&\to &u_{n}\end{matrix}}$

Definición explícita del término general

Representación de una función (trazo continuo) y una sucesión (puntos rojos).

La definición es explícita si u_n está en función de n es decir u_n = f(n).

Representando en la figura los términos de la sucesión, los valores en ordenadas de los puntos rojos y en abscisas hay los enteros naturales .

• Error grave, en ciertos círculos, es nombrar a la extensión en los reales de f por el mismo nombre como se aprecia en la figura, llamémosla por ejemplo P.

La función f(n) comparte propiedades con la extendida P(x) (por ejemplo: límites en el infinito, variaciones, extremos):

• Si $f(n)\xrightarrow {\;\;n\rightarrow \infty \;\;} l$ entonces también lo hace u. La recíproca es errónea, como lo muestra la función p(x) = sin(2πx) no tiene límite para $x\rightarrow \infty$ mientras que u_n = f(n) es siempre 0 y u tiende por lo tanto hacia cero.

• Si p es creciente en un intervalo [a, b] entonces u lo es para los valores enteros positivos del intervalo (o sea sobre [a, b] ∩ $\mathbb {N}$).

En algunos casos u_n = f(n) no puede extenderse a $\mathbb {R}$. Es el caso si definimos u_n como el número de factores propios de n por ejemplo, u otras funciones aritméticas, como la función fi de Euler o la Función de Möbius µ . El estudio clásico de las funciones, mediante la derivación, es entonces imposible.

Definición implícita del término general

La definición es implícita cuando u_n depende de otros términos de la sucesión, que se tendrán que calcular previamente.
Dados u₀, u₁,..., u_n, podemos tener u_i=f(u₁,...,u_n) para i>n.

Es conocida la sucesión de Fibonacci definida por u_n=u_n-1+u_n-2 con n>1 y dado u₀=0, u₁=1.
La fórmula que define un término con relación a los anteriores se llama relación de inducción.

Cuando el término general u_n sólo depende del término anterior , u_n-1, es decir cuando existe f tal que u_n = f(u_n-1) o; lo que viene a ser lo mismo u_n+1 = f(u_n) (para todo natural n), entonces existe un método gráfico de construirla, muy instructivo (ver imagen):

En un sistema de coordenadas se trazan la curva de f y la diagonal (de ecuación y = x). Se empieza por el punto de abscisa del eje horizontal u_o y se sube (o baja) verticalmente hasta encontrar la curva de f. Como u₁ = f(u_o), la ordenada de este punto es u₁. Sin embargo para obtener u₂ necesitamos tener u₁ en las abscisas. Por esto nos desplazamos horizontalmente hasta encontrar la diagonal. En la diagonal, abscisa y ordenada son iguales (por su ecuación y = x), luego bajamos hasta encontrar el eje de las abscisas lo que nos permite leer el valor de u₁. A partir de ahí el proceso se repite igual, pues u₂ = f(u₁) etcétera.

En la práctica, basta trazar la escalera entre la curva y la diagonal para evidenciar el comportamiento de la sucesión ( creciente, decreciente u oscilatoria) y su eventual límite denotado l (ele): si es finito, tiene que ser la abscisa de un punto de intersección de la curva de f y de la diagonal porque tiene que verificar l = f(l), relación obtenida tomando el límite de u_n = f(u_n-1) ( con f continua). Si se acepta la notación f(+ ∞) para designar el límite en el infinito, entonces la relación anterior se extiende tal cual a los infinitos.

Supongamos f continua y derivable en l, límite potencial de la sucesión. Entonces se puede predecir su comportamiento local cerca de l (es decir si u_n es próximo a l, como evoluciona la sucesión a partir de este término). Este comportamiento, en primera aproximación, sólo depende de f '(l), el valor derivado en l:

---

Los tipos de sucesiones más comunes son:

• Las sucesiones aritméticas
• Las sucesiones geométricas
• Las sucesiones aritmeticogeométricas

Las sucesiones aritméticas

Una sucesión aritmética puede ser definida como una función de n:

$u_{n}=u_{0}+r\cdot n\qquad (r\in \mathbb {R} )$

También puede ser definida por inducción de la siguiente forma:

${\begin{matrix}u_{0}&=&a\qquad &(a\in \mathbb {R} )\\u_{n+1}&=&u_{n}+r&(r\in \mathbb {R} )\end{matrix}}$

Al número real r se le denomina razón de la sucesión (revision).

Si la razón es positiva, la sucesión crece, y tiende hacia + ∞. Si es negativa, decrece y tiende hacia - ∞. Si es nula, la sucesión es constante.

Ejemplo:

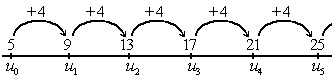
Existe una fórmula muy sencilla para sumar números en progresión aritmética (es decir términos sucesivos de una sucesión aritmética): se multiplica el término medio, que es el promedio de los términos extremos, por el número de términos. Esta fórmula toma las formas siguientes, según el contexto:

$S={\frac {{\mbox{n}}{\acute {\mbox{u}}}{\mbox{mero de t}}{\acute {\mbox{e}}}{\mbox{rminos}}\times ({\mbox{primer t}}{\acute {\mbox{e}}}{\mbox{rmino}}+{\acute {\mbox{u}}}{\mbox{ltimo t}}{\acute {\mbox{e}}}{\mbox{rmino}})}{2}}$

$S=u_{0}+u_{1}+\cdots u_{n}={\frac {(n+1)(u_{0}+u_{n})}{2}}$

$S=u_{1}+u_{2}+\cdots u_{n}={\frac {n(u_{1}+u_{n})}{2}}$

Como caso particular muy frecuente: $1+2+3+\cdots +n={\frac {n(n+1)}{2}}$

A veces lo más difícil es encontrar el número de términos para poder aplicar la fórmula. Si el primer término a sumar vale a, el último vale b, y la razón es r, entonces el número de términos en la suma es:

${\frac {|b-a|}{r}}+1$

Por ejemplo, para la suma: S = 1492 + 1499 + 1506 + ... 2003 de términos consecutivos de una sucesión de razón 7, encontramos ${\frac {2003-1492}{7}}+1=74$ términos, y la suma es ${\frac {74\times (1492+2003)}{2}}=129315$.

Las sucesiones geométricas

Una sucesión geométrica puede ser definida como función de n:

$u_{n}=b\cdot r^{n}\qquad (r\in \mathbb {R} )$

También puede ser definida por inducción de la siguiente forma:

${\begin{matrix}u_{0}&=&b\qquad &(b\in \mathbb {R} )\\u_{n+1}&=&r\cdot u_{n}&(r\in \mathbb {R} )\end{matrix}}$

Al número real r se le denomina también razón de la sucesión. A menudo se la denota q.

Ejemplo:

El comportamiento de la sucesión geométrica depende del signo del primer término y del valor de su razón.

Si la razón es positiva, entonces la sucesión es monótona, y tiene un aspecto muy regular, que se puede prolongar por una función de tipo exponencial de base r: $u_{n}=b\cdot r^{n}$ se prolonga en f(x) = b·r^x.

Se distinguen cuatro casos, como se ve en la figura siguiente; las ordenadas de los puntos negros son los valores de la sucesión, y la curva representa la función:

Si la razón es negativa, entonces la sucesión es oscilante. Se distinguen dos casos en función de si r es menor que -1 ó no. El signo del primer término no modifica el aspecto general de la sucesión (cambiar de signo equivale a una simetría alrededor del eje horizontal, y aquí no se nota mucho). Las potencias rⁿ con r negativo no se generalizan a los reales, salvo convención particular, y por lo tanto no existe una función natural que prolongue la sucesión. En la figura siguiente se ha multiplicado la función |r|^x por el factor cos πx para simular el cambio periódico de signo.

Si el término inicial es nulo, o si la razón vale -1, 0 ó 1, la sucesión no entra en la clasificación anterior, pero no importa pues en tal caso carece de interés.

Descartando estos casos particulares, se puede decir que la convergencia de la sucesión depende del valor absoluto de la razón:

si |r| > 1, no converge, y si |r| < 1, converge hacia cero.

Notemos q la razón, y supongamos q ≠ 1. Entonces la suma de números en progresión geométrica es dada por la fórmula siguiente, bajo tres formas equivalentes:

$S={\frac {{\mbox{primer t}}{\acute {\mbox{e}}}{\mbox{rmino}}-{\mbox{t}}{\acute {\mbox{e}}}{\mbox{rmino que sigue al }}{\acute {\mbox{u}}}{\mbox{ltimo de la suma}}}{1-{\mbox{raz}}{\acute {\mbox{o}}}{\mbox{n}}}}$

$S=u_{0}+u_{1}+\cdots +u_{n}=u_{0}{\frac {1-q^{n+1}}{1-q}}={\frac {u_{0}-u_{n+1}}{1-q}}$

$S=u_{1}+u_{2}+\cdots +u_{n}=u_{1}{\frac {1-q^{n}}{1-q}}={\frac {u_{1}-u_{n+1}}{1-q}}$

Si -1 < q < 1, la suma de todos los términos de la sucesión es: $S={\frac {u_{0}}{1-q}}$.

Fórmulas

Suponiendo que $A_{n}$ sea el término cualquiera, $A_{k}$ el término que ocupa la posición "k", y $A_{1}$ el primer término de la sucesión:

Para hallar un término cualquiera en una sucesión geométrica, se debe usar: $A_{n}=A_{k}\cdot r^{n-k}$

Para sumar los "n" primeros términos de una sucesión geométrica: $S_{n}={\frac {A_{n}\cdot r-A_{1}}{r-1}}$

Para sumar todos los números de una sucesión (Suma infinita): $S_{\infty }={\frac {A_{1}}{1-r}}$ . Esta fórmula sólo es aplicable cuando $\ -1<r<1$

Para calcular el producto de los nº primeros términos de una sucesión: $P_{n}={\sqrt {(A_{n}\cdot A_{1})^{n}}}$

Las sucesiones aritmeticogeométricas

Es, como lo indica su nombre, una mezcla de las dos definiciones anteriores. Se pueden definir por inducción de la siguiente forma:

${\begin{matrix}w_{0}&=&c\qquad \quad \ &(c\in \mathbb {R} )\quad \\w_{n+1}&=&q\cdot w_{n}+r&(q,r\in \mathbb {R} )\end{matrix}}$

La fórmula de inducción hace intervenir la suma de la sucesión aritmética, y el producto de la sucesión geométrica.

Descartemos los casos q = 1 (sucesión aritmética) y r = 0 (sucesión geométrica). Entonces se puede afirmar que el comportamiento de la sucesión es de tipo geométrico, y determinado por q, y que su carácter aritmético solo aparece como una translación.

Más precisamente, sea l el único número que verifica l = ql + r.

Si w₀ = l (lo que equivale a w₁ = w₀ ) entonces w será una sucesión constante. Si no es fácil ver que v₁ = w_n - l es una sucesión geométrica (no nula) de razón q, y que por lo tanto:

si |q| > 1, w no converge (porque no lo hace v)

si |q| < 1, w converge hacia l (porque v tiende hacia 0).

Lógicamente, la clasificación del párrafo anterior según los valores de q sigue siendo válida si trasladamos las curvas verticalmente de l unidades.

Véase también

• Número de Perrin
• Secuencia de Padovan
• Sucesión de Cauchy
• Sucesión de Farey
• Sucesión de Fibonacci
• Sucesión de Goodstein
• Sucesión de Thue-Morse
• Sucesión exacta
• Ecuaciones en diferencias
• Transformada Z
• Serie matemática

Enlaces externos

• Wikimedia Commons alberga una galería multimedia sobre Sucesión.

• Calculo de la fórmula de una Sucesión

---

El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en castellano bajo la licencia GFDL.

---