Vector isótropo
En matemáticas, dado un espacio vectorial X con una forma cuadrática q asociada (denotado como (X, q)), un vector isótropo (o también vector isotrópico) es un elemento x de X distinto de cero, para el que q(x)= 0.
En la teoría de formas bilineales reales, formas bilineales definidas y formas cuadráticas isótropas son distintos. Se distinguen porque solo para este último existe un vector nulo distinto de cero.
Un espacio cuadrático (X, q) que tiene un vector nulo se llama espacio pseudoeuclídeo.
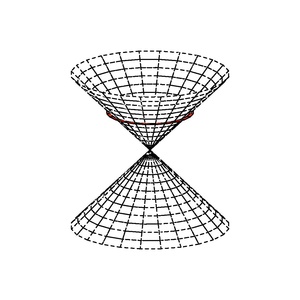
Un espacio vectorial pseudoeuclídeo se puede descomponer (de forma no única) en dos espacios ortogonales A y B, X= A + B, donde q es positivo-definido en A y negativo-definido en B. El cono nulo, o cono isótropo, de X consiste en la unión de esferas equilibradas:
El cono nulo es también la unión de las dos rectas isótropas a través del origen.
Álgebras divididas[editar]
Un álgebra de composición con un vector nulo es un álgebra dividida.[1]
En un álgebra de composición (A, +, ×, *), la forma cuadrática es q(x) = x x*. Cuando x es un vector nulo, entonces no hay inverso multiplicativo para x y, dado que x ≠ 0, A no es un álgebra de división.
En la construcción de Cayley-Dickson, las álgebras divididas surgen en la serie de números bicomplejos, bicuaterniones y bioctoniones, que utiliza el cuerpo de los números complejos como base de esta construcción de duplicación debida a Leonard Eugene Dickson (1919). En particular, estas álgebras tienen dos unidades imaginarias, que conmutan de modo que su producto, cuando se eleva al cuadrado, produce +1:
- Entonces
- y entonces (1 + hi) es un vector nulo.
Las subálgebras reales, los números complejos hiperbólicos, los cuaterniones divididos y los octoniones divididos, con sus conos nulos que representan el seguimiento de la luz dentro y fuera de 0 ∈ A, sugieren la topología del espacio tiempo.
Ejemplos[editar]
- Los vectores como de luz del espacio-tiempo de Minkowski son vectores nulos.
- Los cuatro bicuaterniones independientemente lineales l= (1 + hi), n= (1 + hj), m= (1 + hk) y m∗= (1 – hk) son vectores nulos; y {l, n, m, m∗} puede servir como base para el subespacio utilizado para representar el espacio-tiempo. Los vectores nulos también se utilizan en el enfoque del formalismo de Newman-Penrose para variedades de espacio-tiempo.[2]
- En el módulo de Verma de un álgebra de Lie hay vectores nulos.
Referencias[editar]
- ↑ Arthur A. Sagle & Ralph E. Walde (1973) Introduction to Lie Groups and Lie Algebras, page 197, Academic Press
- ↑ Patrick Dolan (1968) A Singularity-free solution of the Maxwell-Einstein Equations, Communications in Mathematical Physics 9(2):161–8, especially 166, link from Project Euclid
Bibliografía[editar]
- Dubrovin, B. A.; Fomenko, A. T.; Novikov, S. P. (1984). Modern Geometry: Methods and Applications (Robert G. Burns, trad.). Springer. p. 50. ISBN 0-387-90872-2.
- Shaw, Ronald (1982). Linear Algebra and Group Representations 1. Academic Press. p. 151. ISBN 0-12-639201-3.
- Neville, E. H. (Eric Harold) (1922). Prolegomena to Analytical Geometry in Anisotropic Euclidean Space of Three Dimensions. Cambridge University Press. p. 204.





