Trazado de rayos (física)

En física, el trazado de rayos es un método para calcular el camino de ondas o partículas a través de un sistema con regiones de velocidad de propagación variable, de características de absorción heterogéneas, y de superficies reflectoras. Bajo estas circunstancias, los frentes de onda se pueden curvar, cambiar de dirección, o reflejarse en distintas superficies, complicando su análisis. El trazado de rayos soluciona el problema utilizando repetidamente haces estrechos ideales denominados rayos a través del medio en cantidades discretas. Los problemas sencillos pueden ser analizados mediante la propagación de unos cuantos rayos utilizando matemáticas sencillas. Análisis más detallados pueden realizarse utilizando un ordenador para propagar muchos rayos.
Cuando se aplica a problemas de radiación electromagnética, para determinar el trazado de una onda a menudo se confía en soluciones aproximadas de las ecuaciones de Maxwell, que son válidas mientras las ondas de luz se propagan a través de y alrededor de objetos cuyas dimensiones son mucho más grandes que la longitud de onda de la luz. La teoría de rayos no describe fenómenos como la interferencia y la difracción, que requieren la teoría ondulatoria (implicando la fase de las ondas).
Técnica[editar]

El trazado de rayos trabaja suponiendo que la partícula o la onda pueden ser modelizadas como un gran número de haces muy estrechos (rayos), y que existe alguna distancia, posiblemente muy pequeña, sobre la que estos rayos se propagan localmente en línea recta. El trazado de rayos hace avanzar el rayo sobre su alineación, y entonces utiliza una derivada local del medio para calcular la nueva dirección del rayo. Desde esta posición, se envía el rayo adelante de nuevo, y el proceso se repite hasta que se genera un camino completo. Si la simulación incluye objetos sólidos, el rayo puede ser probado por su intersección con estos objetos en cada paso, haciendo ajustes en la dirección del rayo si interviene una colisión. Otras propiedades del rayo pueden ser alteradas, como el paso de avance de la simulación, la intensidad, la longitud de onda, o la polarización. El proceso es repetido con muchos rayos cuando es necesario entender el comportamiento del sistema completo.
Usos[editar]
Señales de radio[editar]
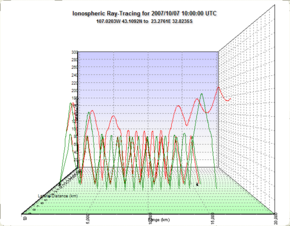
Una forma particular del trazado de rayos es el de una señal de radio, modelizada como rayos a través de la ionosfera, donde son refractados y/o reflejados hacia la Tierra. Modelizar su comportamiento implica la integración de ecuaciones diferenciales que describen la propagación de ondas electromagnéticas a través de medios dispersivos y anisótropos como la ionosfera. Un ejemplo de la física de las señales radiofónicas basado en el trazado de rayos es el mostrado a la derecha. Los estudios de comunicaciones radiofónicas se valen del trazado de radios para determinar el comportamiento preciso de estas señales cuando se propagan a través de la ionosfera.
La imagen de la derecha ilustra la complejidad de la situación. A diferencia del rayo óptico cuyo trazado depende de su paso por un medio que normalmente presenta un índice de refracción constante, el trazado del haz de una señal de radio tiene que tratar las complejidades de un espacio de índice de refracción variable, donde los cambios en la densidad de electrones de la ionosfera influyen en el índice de refracción del medio, y de ahí, en la trayectoria de los rayos. Dos conjuntos de señales son transmitidos con dos elevaciones angulares diferentes. Cuando la señal principal penetra en la ionosfera, el campo magnético parte la señal en dos ondas, que son trazadas separadamente a través de la ionosfera. La componente de la onda normal (color rojo), sigue un camino completamente independiente del camino de la componente de la onda extraordinaria (color verde).
Acústica de los océanos[editar]
La velocidad del sonido en el océano varía con la profundidad debido a cambios en la densidad y en la temperatura del agua, alcanzando un mínimo local a una profundidad de entre 800 y 1000 metros. Este mínimo local, llamado el canal SOFAR, actúa como una guía de ondas, debido a que el sonido tiende a orientarse hacia este canal. El trazado de las ondas de sonido se suele calcular a través del océano hasta distancias muy grandes, incorporando los efectos del canal SOFAR, así como de reflexiones y refracciones de la superficie y del fondo del océano. A partir de esto, la ubicación de las señales de alta y de baja intensidad puede ser calculada, lo que resulta de gran utilidad en los campos de la acústica oceánica, de la comunicación acústica submarina, y de la termometría acústica.

Diseño óptico[editar]
El trazado de rayos puede ser utilizado en el diseño de lentes y sistemas ópticos, como en cámaras fotográficas, microscopios, telescopios, y prismáticos, y su aplicación en este campo data de fechas anteriores al año 1900. El trazado geométrico de rayos suele describir la propagación de los haces de luz a través de un sistema de lentes o instrumentos ópticos, permitiendo modelizar las propiedades del sistema de imagen analizado. Los efectos siguientes pueden ser integrados mediante este tipo de consideraciones geométricas:
- Dispersión, como causa de la aberración cromática
- Polarización
- Efectos de la luz Láser
- Interferencia de película delgada (recubrimiento óptico, burbuja de jabón) se suele usar para calcular la reflectividad de una superficie.
En el diseño de lentes, dos casos especiales de interferencia ondulatoria son importantes para ser tenidos en cuenta. En un punto focal, los rayos procedentes de una fuente de luz puntual se reúnen de nuevo, y pueden interferirse entre sí, constructiva o destructivamente. Dentro de una región muy pequeña cercana a este punto, la luz incidente puede ser aproximada por ondas planas, cuya oscilación se deduce de la dirección de los rayos. La longitud del camino óptico de la fuente de luz se usa para calcular su fase. La derivada de la posición del rayo procedente de la fuente en la región focal permite obtener el ancho del haz, y de este dato la amplitud de la onda plana. El resultado es la función de dispersión de punto, de la que la transformada de Fourier es la función de transferencia óptica. A partir de esta, también puede ser calculado el cociente de Strehl.
El otro caso especial a considerar es el de la interferencia de frentes de onda, que, como ya se ha dicho, se consideran aproximadamente planos. Cuando los rayos se juntan al máximo o incluso se cruzan, sin embargo, el frente de ondas colapsa. La interferencia de ondas esféricas normalmente no se combina con el trazado de rayos, por lo que no permite el cálculo del efecto de difracción producido por una ranura. Aun así, estas limitaciones pueden ser resueltas por una técnica de modelizado avanzada, denominada "trazado de campo". Esta técnica de modelización, combina la óptica geométrica con la óptica física, lo que permite vencer las limitaciones que suponen la interferencia y la difracción en determinados diseños.
Las técnicas de trazado de rayos permiten optimizar el diseño de los instrumentos ópticos, minimizando las aberraciones, en fotografía, y para aplicaciones de longitud de onda más larga como el diseño de microondas o incluso de sistemas radiofónicos, y para longitudes de onda más cortas, como ultravioletas y la óptica de radiología.
Antes de la generalización de los ordenadores, el cálculo del trazado de rayos se efectuaba a mano, utilizando trigonometría y tablas logarítmicas. Las fórmulas ópticas de muchas lentes fotográficas clásicas se optimizaron mediante numerosos operadores manuales, que manejaban partes pequeñas de un cálculo muy grande. Ahora es habitual el software de diseño óptico. Una versión sencilla del trazado de haces conocida como transferencia de rayos matricial es a menudo utilizada en el diseño de los resonadores ópticos utilizados en láseres. Los principios básicos del algoritmo más utilizado se describen en un artículo fundamental de Spencer y Murty titulado: "Procedimiento General del Trazado de Rayos".[1]
Sismología[editar]
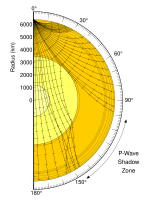
En sismología, los geofísicos utilizan el trazado de rayos para localizar la ubicación de terremotos y la reconstrucción tomográfica del interior de la Tierra.[2][3] La velocidad ondulatoria sísmica varía dentro y debajo de la corteza terrestre, causando que estas ondas se curven y se reflejen. El trazado de rayos computa las trayectorias a través de un modelo geofísico, siguiéndolas atrás hasta alcanzar su fuente, como un terremoto, o deduciendo las propiedades del material por el que se transmiten.[4] En particular, el descubrimiento de la zona de sombra sísmica (ilustrada a la derecha) permitió a los científicos deducir la presencia del núcleo metálico del interior de la Tierra.
Física de plasma[editar]
El transporte de energía y la propagación de ondas juega una función importante en el calentamiento ondulatorio de plasmas. Las trayectorias de flujo de potencia de ondas electromagnéticas a través de un núcleo espacial de plasma no uniforme pueden ser calculadas utilizando soluciones directas de las ecuaciones de Maxwell. Otra manera de computar la propagación de las ondas en el medio de plasma, es utilizar el método de trazado de rayos. Existen estudios de propagación ondulatoria en los plasmas que utilizan este método.[5]
Relatividad general[editar]
En la relatividad general, donde se contemplan lentes gravitacionales, las líneas geodésicas determinadas por el trazado de rayos de luz percibidos por un observador, se integran hacia atrás en el tiempo hasta alcanzar la región de interés.[6][7]
Véase también[editar]
- Refracción atmosférica
- Trazado de campos
- Óptica de índice del gradiente
- Lista de software de trazado de rayos
- Tomografía acústica del océano
- Trazado de rayos (gráfico)
- Análisis matricial de transferencia de rayos
Referencias[editar]
- ↑ G. H. Spencer and M. V. R.K. Murty (1962). «General ray tracing Procedure» (PDF). J. Opt. Soc. Am. 52 (6): 672-678. doi:10.1364/JOSA.52.000672.
- ↑ Rawlinson, N., Hauser, J. and Sambridge, M., 2007. Seismic ray tracing and wavefront tracking in laterally heterogeneous media. Advances in Geophysics, 49. 203–267.
- ↑ Cerveny, V. (2001). Seismic Ray Theory. ISBN 0-521-36671-2.
- ↑ Purdue University
- ↑ Bhaskar Chaudhury and Shashank Chaturvedi (2006). «Comparison of wave propagation studies in plasmas using three-dimensional finite-difference time-domain and ray-tracing methods». Physics of Plasmas 13 (12): 123302. Bibcode:2006PhPl...13l3302C. doi:10.1063/1.2397582.
- ↑ Daniel Kuchelmeister, Thomas Müller, Marco Ament, Günter Wunner, Daniel Weiskopf (2012). «GPU-based four-dimensional general-relativistic ray tracing». Computer Physics Communications, Sciencedirect - doi.org/10.1016/j.cpc.2012.04.030.
- ↑ Thomas Müller (2014). «GeoViS—Relativistic ray tracing in four-dimensional spacetimes». Computer Physics Communications, Sciencedirect - doi.org/10.1016/j.cpc.2014.04.013.
