Teorema de Carnot
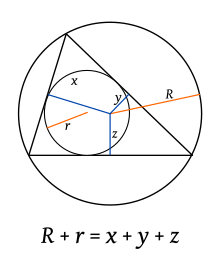

En geometría, el teorema de Carnot, nombrado así por el matemático francés Lazare Carnot (1753-1823), es el siguiente:
Sea ABC un triángulo cualquiera. Entonces la suma de las distancias desde el circuncentro D a los lados del triángulo ABC es
donde r es el radio del círculo inscrito en el triángulo y R es el radio del círculo circunscrito del triángulo. Aquí, el signo de la distancia es negativa si, y solo si el segmento DX (X = F, G, H) esta completamente fuera del triángulo. En la imagen de abajo (el caso de un triángulo obtusángulo) DF es negativo y los segmentos DG y DH son positivos.
Un resultado relacionado con el teorema de Carnot es el primer teorema de Mikami-Kobayashi o teorema japonés de polígonos concíclicos.
Historia[editar]
En 1800, un samurai anónimo colgó en la pared de un templo una tablilla de madera en la que estaba grabado un sangaku, problema de geometría dedicado a una deidad (kami) y propuesto a la sagacidad de los fieles.
En 1803, Carnot publicó su Géométrie de position. Accidente de la historia, un teorema de este libro[1] permite elegantemente resolver el sangaku antes mencionado.
Referencias[editar]
- ↑ Carnot, L. N. M. (1803). Géométrie de position. J. B. M. Duprat. p. 168.

