Sudoku
Sudoku (en japonés: 数独, sūdoku) es un juego matemático que se inventó a finales de la década de 1970, adquirió popularidad en Japón en la década de 1980, y se dio a conocer en el ámbito internacional en 2005, cuando numerosos periódicos empezaron a publicarlo en su sección de pasatiempos.[1]
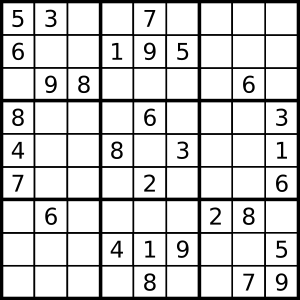
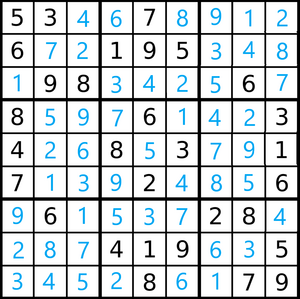
El objetivo del sudoku es rellenar una cuadrícula de 9 × 9 celdas (81 casillas) dividida en subcuadrículas de 3 × 3 (también llamadas "cajas" o "regiones") con las cifras del 1 al 9 partiendo de algunos números ya dispuestos en algunas de las celdas. La forma inicial del juego es que sean nueve elementos diferenciados, que no se deben repetir en una misma fila, columna o subcuadrícula. Un sudoku bien planteado solo puede tener una solución, y ha de tener al menos 17 pistas iniciales.[2] [3] La solución de un sudoku siempre es un cuadrado latino, aunque el recíproco en general no es cierto ya que el sudoku establece la restricción añadida de que no se puede repetir un mismo número en una subcuadrícula.
Historia[editar]
En el siglo XVIII el famoso matemático suizo Leonhard Euler creó un sistema de probabilidades para representar una serie de números sin repetir. Debido a esto, Euler se considera el inventor de este juego.[4]
Ya en 1970 la editorial Math Puzzles and Logic Problems publicaba una sección llamada Number place por lo que este enigma matemático se convertiría en pasatiempos aunque años más tarde se perdió en el olvido.
En 1984 el periódico japonés Monthly Nikolist publicó una sección de pasatiempos llamada Sūji wa dokushin ni kagiru (数字は独身に限る) "los números deben ser únicos" (literalmente dokushin (独身) = "célibe, soltero"). Fue Maki Kaji, presidente de Nikoli, quien le puso el nombre. El nombre se abrevió a Sūdoku (sū = número, doku = solo).[5]
Se comenzó a conocer internacionalmente en 2005, cuando varios periódicos empezaron a publicarlo como pasatiempo.[1]
Reglas y terminología[editar]
El sudoku se presenta normalmente como una tabla de 9 × 9, compuesta por subtablas de 3 × 3 denominadas "regiones" (también se le llaman "cajas" o "bloques").
Algunas celdas ya contienen números, conocidos como "números dados" (o a veces "pistas"). El objetivo es rellenar las celdas vacías, con un número en cada una de ellas, de tal forma que cada columna, fila y región contenga los números 1–9 solo una vez.
Además, cada número de la solución aparece solo una vez en cada una de las tres "direcciones", de ahí el "los números deben estar solos" que evoca el nombre del juego.
Métodos de resolución[editar]
 La casilla marcada en verde de la región 3 × 3 de la esquina superior izquierda debe contener un 7.
La casilla marcada en verde de la región 3 × 3 de la esquina superior izquierda debe contener un 7.
La estrategia para resolver este rompecabezas se puede considerar como la combinación de tres procesos: rastreo, marcado y análisis.

Rastreo[editar]
En el ejemplo anterior, rastreando a lo largo y ancho los sietes localizados en cualquier lugar de la rejilla, el jugador puede eliminar todas las celdas vacías de la esquina superior izquierda que no pueden contener un 7. Esto deja sólo una celda posible (marcada en verde).
Marcado[editar]
El rastreo viene a interrumpirse cuando no pueden descubrirse nuevos números. En este punto es necesario centrarse en algún análisis lógico. La mayoría encuentra útil guiar este análisis mediante el marcado de números candidatos en las celdas vacías. Hay dos notaciones populares: subíndices y puntos.
En la notación de subíndice, los números candidatos se escriben en pequeño en las celdas. La desventaja es que los rompecabezas originales se publican en periódicos que habitualmente no dejan demasiado espacio para acomodar más que unos pocos dígitos. Si se usa esta notación, los resolutores crean, a menudo, una copia más grande del rompecabezas y emplean un lápiz afilado.
La segunda notación es un patrón de puntos con un punto en la esquina superior izquierda representando un 1 y un punto en la esquina inferior derecha representando un 9. Esta notación tiene como ventaja que puede usarse en el rompecabezas original. Se requiere destreza para el emplazamiento de los puntos, porque la existencia de puntos desplazados o marcas inadvertidas lleva, inevitablemente, a confusión y no son fáciles de borrar sin añadir más confusión.
Análisis[editar]
Hay dos aproximaciones principales:
- En eliminación, el progreso se realiza mediante la sucesiva eliminación de números candidatos para una o más celdas, hasta dejar solo una elección. Después de lograr cada respuesta, debe realizarse un nuevo rastreo (habitualmente comprobando el efecto del último número). Hay una serie de tácticas de eliminación. Una de las más comunes es el "borrado del candidato no coincidente". Las celdas con idéntica configuración de números candidatos se dice que coinciden si la cantidad de números candidatos en cada una es igual al número de celdas que los contienen. Esta aproximación puede ser desaprobada por puristas lógicos por demasiado ensayo y error pero puede llegar a soluciones claras y rápidamente.
Idealmente, se necesita encontrar una combinación de técnicas que eviten alguno de los inconvenientes de los elementos de arriba. El recuento de regiones, filas y columnas puede resultar aburrido. Escribir números candidatos en celdas vacías puede consumir demasiado tiempo. La aproximación "y-si" puede ser confusa a menos que se sea bien organizado. La intención de la cuestión es encontrar una técnica que minimice el recuento y el marcado.
Una sistemática análisis de la lógica y de las técnicas de resolución fue publicada in Inglés: "Pattern-Based Constraint Satisfaction and Logic Puzzles".[6]
Niveles de dificultad[editar]
Los programas informáticos que resuelven sudokus pueden estimar la dificultad que tiene un humano para encontrar la solución, basándose en la complejidad de las técnicas de resolución necesarias. Esta estimación permite a los editores adaptar sus sudokus para personas con diferente experiencia resolutoria. Algunas versiones "en línea" (online) también ofrecen varios niveles de dificultad.
Construcción[editar]
Un sudoku debe tener una única solución para que se considere bien planteado; es decir, a partir de las pistas iniciales sólo puede haber una forma válida de completar las casillas restantes. Para que un sudoku posea una única solución, es necesario que el número de pistas iniciales sea al menos 17; esto se demostró en 2012.[3]
La construcción de un sudoku puede ser realizada a mano eficientemente predeterminando las posiciones de los números dados y asignándoles valores para realizar un proceso deductivo.
Los sudokus Nikoli se construyen a mano, y el nombre del autor aparece en los créditos junto a cada rompecabezas; los números dados siempre se encuentran en forma de un patrón simétrico. Los rompecabezas Number Place Challenger de Dell (véase Variantes más abajo) también citan los créditos del autor. Los rompecabezas sudoku que aparecen en la mayoría de los periódicos del Reino Unido aparentemente son generados por ordenador, pero emplean probables en sudokus generados por ordenador. El desafío para los programadores de sudokus es enseñar a un programa cómo construir rompecabezas inteligentes, de manera que no se puedan distinguir de aquellos realizados por humanos; Wayne Gould necesitó retocar su popular programa durante seis años para creer que había alcanzado ese nivel.
Variantes[editar]
Aunque lo más común es que la tabla tenga un tamaño de 9x9 con regiones de 3x3, hay numerosas variantes. Los juegos de iniciación pueden ser tablas de 4x4 con regiones de 2x2; bajo el nombre de Logi-5, se han publicado tablas de 5x5 con pentominós como regiones; el World Puzzle Championship ha publicado una tabla de 6x6 con regiones de 2x3 y una tabla de 7x7 formada por 6 regiones compuestas por heptominós y una región separada. También se pueden encontrar tablas de mayor tamaño. El diario The Times propone el Dodeka Sudoku, una tabla de 12x12 con 12 regiones de 4x3. Dell Magazines publica con frecuencia juegos de 16x16 (la variante de 16x16 utiliza normalmente los símbolos del 1 a la G, en lugar de los símbolos del 0 a la F usados en hexadecimal). El editor de puzles Nikoli propone el Sudoku Gigante de 25x25.


Otra variante frecuente es añadir límites en la colocación de los números aparte de mantener los requisitos normales sobre filas, columnas y regiones. Con frecuencia, los límites toman la forma de una “dimensión” extra; lo más común es obligar a que los números de la diagonal principal de la tabla sean únicos. Los ya mencionados juegos Number Place Challenger incluyen esta variante. También forman parte de esta variante los juegos del Daily Mail que utilizan tablas de 6x6.
El periódico americano USA Today publica otra variante denominada “Mini Sudoku”, consistente en una tabla de 6x6 con regiones de 3x2. El objetivo es el mismo que en el Sudoku original, pero en esta variante solo se utilizan números del 1 al 6.
Otra variante es la combinación del Sudoku y el Kakuro en una tabla de 9x9, denominada Sudoku de Sumas Cruzadas, en la que las pistas se dan a través de sumas cruzadas. También es posible que las pistas se den mediante criptoaritmos en los que cada letra representa un único dígito del 0 al 9. Un ejemplo es: NUMBER+NUMBER=KAKURO cuya única solución es 186925+186925=373850. Otro ejemplo es SUDOKU=IS*FUNNY cuya solución es 426972=34*12558.


El Addoku combina elementos de Sudoku y Kakuro – normalmente no se dan números iniciales, sino que la tabla de 9x9 se divide en regiones, cada una de las cuales contiene la suma de todos los números de la región teniendo además en cuenta que no hay números repetidos en la misma región. A la hora de completar la tabla se mantienen además las reglas del Sudoku original.
Una de las variantes más populares es el Hypersudoku. Se publica en periódicos y revistas de todo el mundo y también es conocido por “Sudoku NRC Handelsblad”, “Windoku”, “Hiper-Sudoku” y “Sudoku 4 cuadros”. La base es idéntica a la del Sudoku original, pero incluye áreas interiores adicionales en las que deben aparecer números del 1 al 9. El algoritmo que lo resuelve es ligeramente diferente del Sudoku normal por la influencia de los cuadros solapados. Este solapamiento da al jugador más información que permite reducir las posibilidades de los restantes cuadros. La forma de jugar es similar a la del Sudoku pero es necesario prestar más atención a las cuadros y a las zonas solapadas que a las filas y columnas.

También son comunes los juegos construidos a partir de múltiples tablas de Sudoku. En Japón es conocido el Sudoku Gattai 5 (mezcla de 5) compuesto por 5 tablas de 9x9 con solapamiento en las regiones de las esquinas con forma de quincuncio. En diarios como The Times o The Sydney Morning Herald, esta variante se conoce como Sudoku Samurai. Otros como el Baltimore Sun y el Toronto Star publican esta variante en su edición dominical con el nombre High Five. Con frecuencia, no se proporcionan pistas en las regiones solapadas. También se publican variantes con tablas secuenciales, en lugar de solapadas, en las que los valores de determinadas posiciones se transfieren de una tabla a otra.
El Sudoku Social es una versión digital multijugador de Sudoku que permite a 2 jugadores jugar al mismo tiempo sobre el mismo tablero. Esta variante fue creada por Crosswords Ltd. en 2010 y lanzada como aplicación para la plataforma iOS de Apple a través de su Game Center. El Sudoku Social[2] concede puntos a cada jugador a medida que van colocando los números correctamente, bloqueando el cuadro seleccionado al otro jugador. Las jugadas incorrectas hacen que el jugador no tenga acceso al tablero durante 10 segundos, además de provocar la pérdida de puntos.
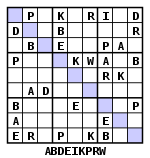
También han surgido variantes alfabéticas, llamadas a veces Sudokus de letras (Wordokus): no existe diferencia funcional a menos que las letras formen palabras. Algunas variantes, como la de TV Guide, incluyen una vez resuelto el juego una palabra en la diagonal principal, en una fila o en una columna; determinar la palabra por adelantado puede ser una ayuda para la resolución del juego. Un Wordoku puede contener otras palabras además de la palabra principal. Como en el ejemplo de la derecha, las palabras “Kari”, “Park” y “Per” podrían formar parte de la solución. Esto debería evitarse sustituyendo, por ejemplo, el carácter “R” por el carácter “Q”. Por otro lado el Sudoku Ripeto permite repetir símbolos y el Custom Sudoku mostrar palabras en el tablero antes de la resolución.

Otra variante sin diferencia funcional es el Quadratum Latinum con Numeración romana de Hebdomada Aenigmatum, la revista de crucigramas íntegramente en latín de Luca Desiata.[7]
Con una baraja estándar de 81 cartas del juego Set! puede jugarse al Sudoku. La versión tridimensional del Sudoku fue inventada por Dion Church y publicada en el Daily Mail Telegraph en mayo de 2005. También existe una versión del cubo de Rubik denominada el cuboku.
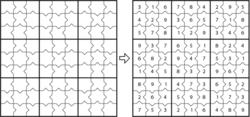
Hay otras muchas variantes. Algunas presentan diferentes formas en la disposición de los solapamientos de tablas de 9x9, tales como una mariposa, un molino o una flor.[8] Otras versiones varían en la lógica de resolución del juego. Una de ellas es Sudoku Mayor que. En esta versión, cada región de 3x3 contiene 12 símbolos de mayor (>) o menor (<) en la línea común de dos números adyacentes.[9] Otra variante de este tipo es Sudoku Sin pistas en el que se colocan nueve tablas de Sudoku de 9x9 en una matriz de 3x3. La celda central de cada región de 3x3 en cada una de las 9 tablas se deja en blanco, formando un décimo Sudoku sin ninguna celda completa; de ahí el nombre "sin pistas".[8]
Véase también[editar]
Referencias[editar]
- ↑ a b Tony Crilly (2011). 50 cosas que hay que saber sobre matemáticas. Ed. Ariel. ISBN 978-987-1496-09-9.
- ↑ "Las claves matemáticas para resolver un sudoku", en Abc, 10/01/2012. [1] Un sudoku no se puede resolver si no hay un mínimo de 17 cifras-pista en su inicio, ya que con menos "no existe una solución única". La mayor parte de las veces cuenta con unas 25 cifras-pista. A medida que bajan las pistas, más difícil es su resolución.
- ↑ a b Gary McGuire, Bastian Tugemann, Gilles Civario (2013). «There is no 16-Clue Sudoku: Solving the Sudoku Minimum Number of Clues Problem via Hitting Set Enumeration» (en inglés). Consultado el 5 de noviembre de 2021.
- ↑ Stark, Florian (15 de abril de 2013). «Wahrer Erfinder des Sudoku war ein Schweizer» (en alemán). Consultado el 24 de febrero de 2020.
- ↑ «Historia del Sudoku». Archivado desde el original el 24 de septiembre de 2015. Consultado el 26 de julio de 2011.
- ↑ Denis Berthier (2012). Pattern-Based Constraint Satisfaction and Logic Puzzles. Lulu.com Publishers. ISBN 978-1-291-20339-4.
- ↑ Sitio oficial de Hebdomada Aenigmatum
- ↑ a b «www.janko.at».
- ↑ Pegg, Ed, Jr. (15 de septiembre de 2005). «Ed Pegg Jr.'s Math Games: Sudoku Variations». MAA Online. The Mathematical Association of America. Archivado desde el original el 3 de octubre de 2005. Consultado el 3 de octubre de 2006.
