De Wikipedia, la enciclopedia libre
Distribución triangular
Función de densidad de probabilidad
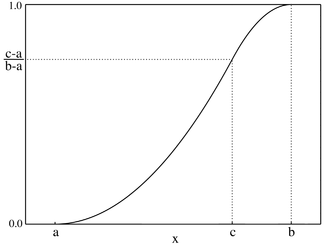
Función de distribución de probabilidad Parámetros
a
:
a
∈
(
−
∞
,
∞
)
{\displaystyle a:~a\in (-\infty ,\infty )}
b
:
a
<
b
{\displaystyle b:~a<b\,}
c
:
a
≤
c
≤
b
{\displaystyle c:~a\leq c\leq b\,}
Función de densidad (pdf)
{
0
para
x
<
a
,
2
(
x
−
a
)
(
b
−
a
)
(
c
−
a
)
para
a
≤
x
<
c
,
2
b
−
a
para
x
=
c
,
2
(
b
−
x
)
(
b
−
a
)
(
b
−
c
)
para
c
<
x
≤
b
,
0
para
b
<
x
.
{\displaystyle {\begin{cases}0&{\text{para }}x<a,\\{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{para }}a\leq x<c,\\[4pt]{\frac {2}{b-a}}&{\text{para }}x=c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{para }}c<x\leq b,\\[4pt]0&{\text{para }}b<x.\end{cases}}}
Función de distribución (cdf)
{
0
para
x
≤
a
,
(
x
−
a
)
2
(
b
−
a
)
(
c
−
a
)
para
a
<
x
≤
c
,
1
−
(
b
−
x
)
2
(
b
−
a
)
(
b
−
c
)
para
c
<
x
<
b
,
1
para
b
≤
x
.
{\displaystyle {\begin{cases}0&{\text{para }}x\leq a,\\[2pt]{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{para }}a<x\leq c,\\[4pt]1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{para }}c<x<b,\\[4pt]1&{\text{para }}b\leq x.\end{cases}}}
Media
a
+
b
+
c
3
{\displaystyle {\frac {a+b+c}{3}}}
Mediana
{
a
+
(
b
−
a
)
(
c
−
a
)
2
para
c
≥
a
+
b
2
,
b
−
(
b
−
a
)
(
b
−
c
)
2
para
c
≤
a
+
b
2
.
{\displaystyle {\begin{cases}a+{\frac {\sqrt {(b-a)(c-a)}}{\sqrt {2}}}&{\text{para }}c\geq {\frac {a+b}{2}},\\[6pt]b-{\frac {\sqrt {(b-a)(b-c)}}{\sqrt {2}}}&{\text{para }}c\leq {\frac {a+b}{2}}.\end{cases}}}
Moda
c
{\displaystyle c}
Varianza
a
2
+
b
2
+
c
2
−
a
b
−
a
c
−
b
c
18
{\displaystyle {\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{18}}}
Curtosis
−
3
5
{\displaystyle -{\frac {3}{5}}}
Entropía
1
2
+
ln
(
b
−
a
2
)
{\displaystyle {\frac {1}{2}}+\ln \left({\frac {b-a}{2}}\right)}
Función generadora de momentos (mgf)
2
(
b
−
c
)
e
a
t
−
(
b
−
a
)
e
c
t
+
(
c
−
a
)
e
b
t
(
b
−
a
)
(
c
−
a
)
(
b
−
c
)
t
2
{\displaystyle 2{\frac {(b\!-\!c)e^{at}\!-\!(b\!-\!a)e^{ct}\!+\!(c\!-\!a)e^{bt}}{(b-a)(c-a)(b-c)t^{2}}}}
Función característica
−
2
(
b
−
c
)
e
i
a
t
−
(
b
−
a
)
e
i
c
t
+
(
c
−
a
)
e
i
b
t
(
b
−
a
)
(
c
−
a
)
(
b
−
c
)
t
2
{\displaystyle -2{\frac {(b\!-\!c)e^{iat}\!-\!(b\!-\!a)e^{ict}\!+\!(c\!-\!a)e^{ibt}}{(b-a)(c-a)(b-c)t^{2}}}}
En probabilidad y estadística , la distribución triangular es una familia de distribuciones continuas de probabilidad que tiene un valor mínimo a , un valor máximo b y una moda c , de modo que la función de densidad de probabilidad es cero para los extremos (a y b ), y afín entre cada extremo y la moda, por lo que su gráfico es un triángulo .
El texto que sigue es una traducción defectuosa. Si quieres colaborar con Wikipedia, busca el artículo original y mejora esta traducción . Copia y pega el siguiente código en la página de discusión del autor de este artículo : {{subst:Aviso mal traducido|Distribución triangular}} ~~~~
1757 … Simpson discutió varias posibles distribuciones de error. Lo primero que consideró fue la distribución uniforme , seguida por la distribución triangular continua simétrica
La función densidad de probabilidad es
f
(
x
|
a
,
b
,
c
)
=
{
2
(
x
−
a
)
(
b
−
a
)
(
c
−
a
)
para
a
≤
x
<
c
,
2
b
−
a
para
x
=
c
,
2
(
b
−
x
)
(
b
−
a
)
(
b
−
c
)
para
c
<
x
≤
b
,
0
para otros casos
{\displaystyle f(x|a,b,c)={\begin{cases}{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{para }}a\leq x<c,\\[4pt]{\frac {2}{b-a}}&{\text{para }}x=c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{para }}c<x\leq b,\\[4pt]0&{\text{para otros casos}}\end{cases}}}
[ editar ] Parámetros:
a
:
a
∈
(
−
∞
,
∞
)
{\displaystyle a\colon a\in (-\infty ,\infty )}
b
:
b
>
a
{\displaystyle b\colon b>a}
c
:
a
≤
c
≤
b
{\displaystyle c\colon a\leq c\leq b}
Soporte:
a
≤
x
≤
b
{\displaystyle a\leq x\leq b}
Función de probabilidad acumulada : =
{
0
para
x
≤
a
,
(
x
−
a
)
2
(
b
−
a
)
(
c
−
a
)
para
a
<
x
≤
c
,
1
−
(
b
−
x
)
2
(
b
−
a
)
(
b
−
c
)
para
c
<
x
<
b
,
1
para
b
≤
x
.
{\displaystyle {\begin{cases}0&{\text{para }}x\leq a,\\[2pt]{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{para }}a<x\leq c,\\[4pt]1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{para }}c<x<b,\\[4pt]1&{\text{para }}b\leq x.\end{cases}}}
Media:
a
+
b
+
c
3
{\displaystyle {\frac {a+b+c}{3}}}
Mediana:
{
a
+
(
b
−
a
)
(
c
−
a
)
2
para
c
≥
a
+
b
2
b
−
(
b
−
a
)
(
b
−
c
)
2
para
c
≤
a
+
b
2
{\displaystyle {\begin{cases}a+{\frac {\sqrt {(b-a)(c-a)}}{\sqrt {2}}}&{\text{para }}c\geq {\frac {a+b}{2}}\\[4pt]b-{\frac {\sqrt {(b-a)(b-c)}}{\sqrt {2}}}&{\text{para }}c\leq {\frac {a+b}{2}}\end{cases}}}
Moda:
c
{\displaystyle c}
Varianza:
a
2
+
b
2
+
c
2
−
a
b
−
a
c
−
b
c
18
{\displaystyle {\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{18}}}
Restricciones:
2
(
a
+
b
−
2
c
)
(
2
a
−
b
−
c
)
(
a
−
2
b
+
c
)
5
(
a
2
+
b
2
+
c
2
−
a
b
−
a
c
−
b
c
)
3
2
{\displaystyle {\frac {{\sqrt {2}}(a\!+\!b\!-\!2c)(2a\!-\!b\!-\!c)(a\!-\!2b\!+\!c)}{5(a^{2}\!+\!b^{2}\!+\!c^{2}\!-\!ab\!-\!ac\!-\!bc)^{\frac {3}{2}}}}}
Curtosis :
−
3
5
{\displaystyle -{\frac {3}{5}}}
Entropía:
1
2
+
ln
(
b
−
a
2
)
{\displaystyle {\frac {1}{2}}+\ln \left({\frac {b-a}{2}}\right)}
Función generadora de momentos :
2
(
b
−
c
)
e
a
t
−
(
b
−
a
)
e
c
t
+
(
c
−
a
)
e
b
t
(
b
−
a
)
(
c
−
a
)
(
b
−
c
)
t
2
{\displaystyle 2{\frac {(b\!-\!c)e^{at}\!-\!(b\!-\!a)e^{ct}\!+\!(c\!-\!a)e^{bt}}{(b-a)(c-a)(b-c)t^{2}}}}
Función característica:
−
2
(
b
−
c
)
e
i
a
t
−
(
b
−
a
)
e
i
c
t
+
(
c
−
a
)
e
i
b
t
(
b
−
a
)
(
c
−
a
)
(
b
−
c
)
t
2
{\displaystyle -2{\frac {(b\!-\!c)e^{iat}\!-\!(b\!-\!a)e^{ict}\!+\!(c\!-\!a)e^{ibt}}{(b-a)(c-a)(b-c)t^{2}}}}
[ editar ] La distribución triangular es habitualmente empleada como una descripción subjetiva de una población para la que sólo se cuenta con una cantidad limitada de datos muestrales y, especialmente en casos en que la relación entre variables es conocida pero los datos son escasos (posiblemente porque es alto el costo de recolectarlos). Está basada en un conocimiento del mínimo y el máximo y un "pálpito inspirado"[ 1]





![{\displaystyle {\begin{cases}0&{\text{para }}x<a,\\{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{para }}a\leq x<c,\\[4pt]{\frac {2}{b-a}}&{\text{para }}x=c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{para }}c<x\leq b,\\[4pt]0&{\text{para }}b<x.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60de66061af39d704dd2c8b64f6655c74e96d3cf)
![{\displaystyle {\begin{cases}0&{\text{para }}x\leq a,\\[2pt]{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{para }}a<x\leq c,\\[4pt]1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{para }}c<x<b,\\[4pt]1&{\text{para }}b\leq x.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d75a71c60263a30588c5049a2e2781760b792b8)

![{\displaystyle {\begin{cases}a+{\frac {\sqrt {(b-a)(c-a)}}{\sqrt {2}}}&{\text{para }}c\geq {\frac {a+b}{2}},\\[6pt]b-{\frac {\sqrt {(b-a)(b-c)}}{\sqrt {2}}}&{\text{para }}c\leq {\frac {a+b}{2}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17c6b74284a45c260ec778f16fd6c2caf27c0381)






![{\displaystyle f(x|a,b,c)={\begin{cases}{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{para }}a\leq x<c,\\[4pt]{\frac {2}{b-a}}&{\text{para }}x=c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{para }}c<x\leq b,\\[4pt]0&{\text{para otros casos}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d98a7f492ddb4a6385b04c408818513b88cbba30)




![{\displaystyle {\begin{cases}a+{\frac {\sqrt {(b-a)(c-a)}}{\sqrt {2}}}&{\text{para }}c\geq {\frac {a+b}{2}}\\[4pt]b-{\frac {\sqrt {(b-a)(b-c)}}{\sqrt {2}}}&{\text{para }}c\leq {\frac {a+b}{2}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19f39dbf94967651be62362fed21b4470536bf2a)
