Flujo
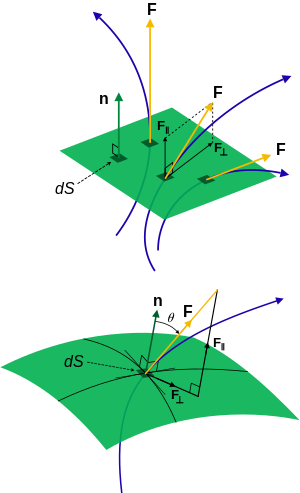
Arriba: Tres líneas de campo que pasan por una superficie plana, una normal a la superficie, una paralela y una intermedia.
Abajo: Línea de campo a través de una superficie, que muestra la configuración de la unidad normal y el elemento de superficie para calcular el flujo.
El término flujo describe cualquier efecto que parece pasar o viajar (ya sea que realmente se mueva o no) a través de una superficie o sustancia. Es un concepto propio del cálculo vectorial y de la matemática aplicada, que aparece en numerosos campos de la física. Para fenómenos de transporte, el flujo es una cantidad vectorial que describe la magnitud y la dirección del flujo de una sustancia o propiedad. En cálculo vectorial el flujo es una cantidad escalar, definida como la integral de superficie de la componente perpendicular de un campo vectorial sobre una superficie.[1]
Terminología
[editar]La palabra flujo proviene del latín fluxus, que significa "flujo"; y de fluere, con el significado de "fluir".[2] El término fluxión, fue introducido en el cálculo diferencial por Isaac Newton.
El concepto de flujo de calor fue una contribución clave de Joseph Fourier en el análisis de los fenómenos de transferencia de calor.[3] En su tratado fundamental Théorie analytique de la chaleur (La teoría analítica del calor),[4] define el flujo como una cantidad central y procede a derivar las ahora bien conocidas expresiones de flujo en términos de diferencias de temperatura a través de una losa, y luego, de manera más general, en términos de gradientes de temperatura o diferenciales de temperatura, a través de otras geometrías. Se podría argumentar, basándose en el trabajo de James Clerk Maxwell,[5] que la definición de transporte precede a la definición de flujo utilizada en electromagnetismo. La cita específica de Maxwell es:
En el caso de los flujos, debemos tomar la integral, sobre una superficie, del flujo que pasa por cada elemento de la superficie. El resultado de esta operación se llama integral de superficie del flujo. Representa la cantidad que pasa por la superficie.James Clerk Maxwell
Según la definición de transporte, el flujo puede ser un único vector o puede ser un campo vectorial/función de posición. En el último caso, el flujo se puede integrar fácilmente sobre una superficie. Por el contrario, según la definición de electromagnetismo, el flujo es la integral sobre una superficie. No tiene sentido integrar un flujo de acuerdo con la segunda definición, ya que sería integrar dos veces sobre una superficie. Por lo tanto, la cita de Maxwell solo tiene sentido si se utiliza la palabra flujo de acuerdo con la definición de transporte (y además es un campo vectorial en lugar de un vector único). Esto es irónico, porque Maxwell fue uno de los principales desarrolladores de los conceptos que ahora se conocen como flujo eléctrico y flujo magnético según la definición del electromagnetismo. Sus nombres de acuerdo con la cita (y la definición de transporte) serían integral de superficie de flujo eléctrico e integral de superficie de flujo magnético, en cuyo caso flujo eléctrico se definiría como campo eléctrico y flujo magnético se definiría como campo magnético. Esto implica que Maxwell concibió estos campos como flujos de algún tipo.
Dado un flujo según la definición empleada en electromagnetismo, la densidad de flujo correspondiente, si se usa ese término, se refiere a su derivada en la superficie que se integró. Según el teorema fundamental del cálculo, la densidad de flujo correspondiente es un flujo según la definición de transporte. Dada una corriente como la corriente eléctrica (carga por tiempo), la densidad de corriente también sería un flujo según la definición de transporte: carga por tiempo por área. Debido a las definiciones contradictorias de flujo y a la intercambiabilidad de flujo y corriente en el lenguaje no técnico, todos los términos utilizados en este párrafo a veces se usan indistinta y ambiguamente. En el resto de este artículo, la palabra flujo se utilizará de acuerdo con su aceptación amplia en la bibliografía, independientemente de a qué definición corresponda el término.
Flujo como caudal por unidad de área
[editar]En fenómenos de transporte (como la transferencia de calor, la transferencia de masa y la fluidodinámica), el flujo se define como la tasa de paso de una propiedad por unidad de área, que tiene dimensiones [cantidad]·[tiempo]−1·[área]−1.[6] El área es la superficie por la que la propiedad fluye a través. Por ejemplo, la cantidad de agua que fluye a través de una sección transversal de un río cada segundo dividida por el área de esa sección transversal, o la cantidad de energía solar que cae sobre una porción de terreno cada segundo dividida por el área de la porción considerada, son tipos de flujo.
Definición matemática general (transporte)
[editar]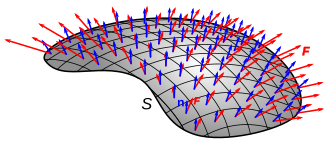
Aparecen tres definiciones en orden creciente de complejidad. Cada una es un caso especial de los que figuran a continuación. En todos ellos se utiliza el símbolo frecuente j (o J) para el flujo, q para la magnitud física que fluye, t para el tiempo y A para el área. Estos identificadores se escribirán en negrita cuando y solo cuando sean vectores.
Primero, el flujo como un escalar (único):
donde
En este caso, la superficie en la que se mide el flujo es fija y tiene un área A. Se supone que la superficie es plana y que el flujo es constante en todas partes con respecto a la posición, y perpendicular a la superficie.
En segundo lugar, el flujo como campo escalar definido en una superficie, es decir, una función de puntos en la superficie:
Como antes, se supone que la superficie es plana y que el flujo es perpendicular a ella en todas partes. Sin embargo, el flujo no tiene por qué ser constante. q es ahora una función de p, un punto en la superficie, y A, un área. En lugar de medirse el flujo total a través de la superficie, q mide el flujo a través del disco de la superficie con el área A y centrado en el punto p.
Finalmente, el flujo como campo vectorial:
En este caso, no hay ninguna superficie fija sobre la que se esté midiendo. q es función de un punto, un área y una dirección (dada por un vector unitario ) y mide el flujo a través del disco de área A perpendicular a ese vector unitario. I se define eligiendo el vector unitario que maximiza el flujo alrededor del punto, porque el flujo real se maximiza a través del disco que es perpendicular a él. Por lo tanto, el vector unitario maximiza de forma única la función cuando apunta en la verdadera dirección del flujo. Estrictamente hablando, este es un abuso de notación, porque "arg max" no puede comparar vectores directamente; en su lugar, se toma el vector con la norma más grande.
Propiedades
[editar]Estas definiciones directas, especialmente la última, son bastante difíciles de manejar. Por ejemplo, la construcción arg max es artificial desde la perspectiva de las mediciones empíricas, cuando con una veleta o similar se puede deducir fácilmente la dirección del flujo en un punto. En lugar de definir directamente el flujo vectorial, suele ser más intuitivo enunciar algunas propiedades al respecto. Además, a partir de estas propiedades se puede determinar de todos modos el flujo de forma inequívoca.
Si el flujo j pasa a través del área formando un ángulo θ con el área normal , entonces el producto escalar
Es decir, la componente del flujo que pasa a través de la superficie (es decir, normal a ella) es j cos θ, mientras que la componente del flujo que pasa tangencial al área es j sin θ, pero ningún flujo realmente pasa a través del área en dirección tangencial. El único componente del flujo que pasa normal al área es la componente del coseno.
Para el flujo vectorial, la integral de superficie de j sobre una superficie S, se obtiene el flujo normal por unidad de tiempo a través de la superficie:
donde A (y su infinitesimal) es la combinación del vector de área (producto de la magnitud del área A por la que pasa la propiedad y del vector unitario normal al área). A diferencia del segundo conjunto de ecuaciones, aquí la superficie no tiene por qué ser plana.
Finalmente, se puede integrar nuevamente durante el tiempo t1 a t2, obteniéndose la cantidad total de la propiedad que fluye a través de la superficie en ese tiempo (t2 − t1):
Flujos de transporte
[editar]Ocho de las formas más comunes de flujo de la bibliografía sobre fenómenos de transporte se definen de la siguiente manera:
- Flujo de momento, la tasa de transferencia de cantidad de movimiento a través de una unidad de área (N·s·m−2·s−1). (Ley de Newton de la viscosidad)[7]
- Flujo de calor, la tasa de flujo de calor a través de una unidad de área (J·m−2·s−1). (Ley de Fourier de la conducción)[8] (Esta definición de flujo de calor se ajusta a la definición original de Maxwell).[5]
- Leyes de Fick, la tasa de movimiento de moléculas a través de una unidad de área (mol·m−2·s−1). (Leyes de Fick)[7]
- Flujo volumétrico, la tasa de flujo de volumen a través de una unidad de área (m3·m−2·s−1). (Ley de Darcy del flujo de aguas subterráneas)
- Flujo de masa, la tasa de flujo de masa a través de una unidad de área (kg·m−2·s−1). (O una forma alternativa de la ley de Fick que incluye la masa molecular, o una forma alternativa de la ley de Darcy que incluye la densidad).
- Flujo radiante, la cantidad de energía transferida en forma de fotones a una cierta distancia de la fuente por unidad de área por segundo (J·m−2·s−1). Se utiliza en astronomía para determinar la magnitud y la clasificación estelar de una estrella. También actúa como una generalización del flujo de calor, que es igual al flujo radiante cuando se restringe al espectro electromagnético.
- Flujo de energía, la tasa de transferencia de energía a través de una unidad de área (J·m−2·s−1). El flujo radiante y el flujo de calor son casos específicos del flujo de energía.
- Flujo de partículas, la tasa de transferencia de partículas a través de una unidad de área ([número de partículas] m−2·s−1)
Estos flujos son vectores en cada punto del espacio y tienen una magnitud y dirección definidas. Además, se puede tomar la divergencia de cualquiera de estos flujos para determinar la tasa de acumulación de la cantidad en un volumen de control alrededor de un punto determinado en el espacio. Para el caso de un flujo incompresible, la divergencia del flujo de volumen es cero.
Difusión química
[editar]Como se mencionó anteriormente, el flujo molar químico de un componente A en un proceso isotérmico e isobárico se define en las leyes de Fick como:
donde el símbolo nabla ∇ denota el operador gradiente, DAB es el coeficiente de difusión (m2·s−1) del componente A que se difunde a través del componente B, cA es la concentración (mol/m3) del componente A.[9]
Este flujo tiene unidades de mol·m−2·s−1 y se ajusta a la definición original de flujo de Maxwell.[5]
Para gases diluidos, la teoría cinética molecular relaciona el coeficiente de difusión D con la densidad de partículas n = N/V, la masa molecular m, la sección eficaz de colisión y la temperatura absoluta T por
donde el segundo factor es el camino libre medio y la raíz cuadrada (con la constante de Boltzmann k) es la velocidad media de las partículas.
En flujos turbulentos, el transporte por movimiento de remolinos se puede expresar como un coeficiente de difusión muy aumentado.
Mecánica cuántica
[editar]En mecánica cuántica, las partículas de masa m en estado cuántico ψ(r, t) tienen un densidad de probabilidad definida como
Entonces, la probabilidad de encontrar una partícula en un elemento de volumen diferencial d3r es
Entonces, el número de partículas que pasan perpendicularmente a través de la unidad de área de una sección transversal por unidad de tiempo es la probabilidad de flujo
Esto a veces se denomina corriente de probabilidad o densidad de corriente,[10] o también densidad de flujo de probabilidad.[11]
Flujo como integral de superficie
[editar]Definición matemática general (integral de superficie)
[editar]
Como concepto matemático, el flujo está representado por la integral de superficie de un campo vectorial,[12]
donde F es un campo vectorial, y dA es el vector de área de la superficie A, dirigido como normal a la superficie. Para la segunda ecuación, n es la normal que apunta hacia afuera de la superficie.
La superficie debe ser orientable, es decir, se pueden distinguir dos lados, de manera que no se pliega sobre sí misma. Además, tiene que estar realmente orientada, es decir, se utiliza una convención en cuanto al sentido en el que el flujo se considera positivo (de manera que el flujo en sentido contrario se considera entonces como negativo).
La normal de superficie suele estar dirigida por la regla de la mano derecha.
Por el contrario, se puede considerar el flujo como la cantidad más fundamental y llamar al campo vectorial densidad de flujo.
A menudo, un campo vectorial se dibuja mediante curvas (líneas de campo) que sigue el flujo. La magnitud del campo vectorial es entonces la densidad de líneas y el flujo a través de una superficie es el número de líneas que la atraviesan. Las líneas se originan en áreas de divergencia positiva (fuentes) y terminan en áreas de divergencia negativa (sumideros).
Véase también la imagen de la derecha: el número de flechas rojas que pasan a través de una unidad de área es la densidad de flujo, la curva que rodea las flechas rojas denota el límite de la superficie y la orientación de las flechas con respecto a la superficie denota el signo del producto interno del campo vectorial con las normales de la superficie.
Si la superficie encierra una región 3D, normalmente la superficie se orienta de manera que el influjo se cuente como positivo; lo contrario es la salida.
El teorema de la divergencia establece que el flujo de salida neto a través de una superficie cerrada, en otras palabras, el flujo de salida neto desde una región 3D, se encuentra sumando el flujo de salida neto local desde cada punto de la región (que se expresa mediante la divergencia).
Si la superficie no está cerrada, tiene como límite una curva orientada. El teorema de Stokes establece que el flujo del rotacional de un campo vectorial es la integral de línea del campo vectorial sobre este límite. Esta integral de trayectoria también se llama circulación, especialmente en dinámica de fluidos. Por tanto, el rotacional es la densidad de la circulación.
Se puede aplicar el flujo y estos teoremas a muchas disciplinas en las que aparecen magnitudes vectoriales (como corrientes o fuerzas) aplicadas a través de áreas.
Electromagnetismo
[editar]Flujo eléctrico
[editar]Una "carga" eléctrica, como un solo protón en el espacio, tiene una magnitud definida en culombios. Tal carga tiene un campo eléctrico que la rodea. En forma gráfica, el campo eléctrico de una carga puntual positiva se puede visualizar como un punto que irradia líneas de campo eléctrico (a veces también llamadas "líneas de fuerza"). Conceptualmente, se puede considerar el flujo eléctrico como "el número de líneas de campo" que pasan por un área determinada. Matemáticamente, el flujo eléctrico es la integral de la componente normal del campo eléctrico en un área determinada. Por lo tanto, las unidades de flujo eléctrico son, en el sistema MKS, newtons por culombio por metro cuadrado, o N m2/C. La densidad de flujo eléctrico es el flujo eléctrico por unidad de área y es una medida de la intensidad de la componente normal del campo eléctrico promediada sobre el área de integración. Sus unidades son N/C, igual que el campo eléctrico en unidades MKS.
Se utilizan dos formas de flujo eléctrico, una para el campo E:[13][14]
y otra para el campo D (llamado densidad de flujo eléctrico):
Esta cantidad surge en la ley de Gauss, que establece que el flujo del campo eléctrico E que sale de una superficie es proporcional a la carga eléctrica AX encerrada en la superficie (independientemente de cómo se distribuya esa carga), la forma integral es:
donde ε0 es la permitividad del vacío.
Si se considera el flujo del vector de campo eléctrico, E, para un tubo cerca de una carga puntual en el campo de la carga pero que no la contiene con lados formados por líneas tangentes al campo, el flujo a través de los lados es cero, y se localiza un flujo igual y opuesto en ambos extremos del tubo. Esto es una consecuencia de la ley de Gauss aplicada a un campo inversamente cuadrático. El flujo para cualquier superficie transversal del tubo será el mismo. El flujo total para cualquier superficie que rodee una carga q es q/ε0.[15]
En el vacío, la densidad de flujo eléctrico viene dada por la ecuación constitutiva D = ε0 E, por lo que para cualquier superficie delimitadora el flujo del campo D es igual a la carga QA dentro de él. Aquí, la expresión "flujo de" indica una operación matemática y, como puede verse, el resultado no es necesariamente un "flujo", ya que en realidad nada fluye en las líneas de campo eléctrico.
Flujo magnético
[editar]La densidad de flujo magnético (campo magnético) que tiene la unidad Wb/m2 (Tesla) se denota por B, y el flujo magnético se define de manera análoga:[13][14]
con la misma notación anterior. La cantidad surge en la ley de Faraday, donde el flujo magnético depende del tiempo, ya sea porque el límite depende del tiempo o porque el campo magnético depende del tiempo. En forma integral:
donde dℓ es un vector infinitesimal elemento de línea de la curva , siendo su magnitud igual a la longitud del elemento de línea infinitesimal, y dirección dada por la tangente a la curva , con el signo determinado por la dirección de la integración.
La tasa de cambio temporal del flujo magnético a través de un bucle de alambre es la fuerza electromotriz con signo negativo creada en ese alambre. La dirección es tal que si se permite que la corriente pase a través del cable, la fuerza electromotriz provocará una corriente que "se opone" al cambio en el campo magnético, produciendo por sí misma un campo magnético opuesto al cambio. Esta es la base del principio de inducción y de muchos generadores eléctricos.
Flujo de Poynting
[editar]Usando esta definición, el flujo del vector de Poynting S sobre una superficie específica es la velocidad a la que la energía electromagnética fluye a través de esa superficie, definida como antes:[14]
El flujo del vector de Poynting a través de una superficie es la potencia electromagnético, o energía por unidad de tiempo, que pasa a través de esa superficie. Esto se usa comúnmente en el análisis de la radiación electromagnética, pero también tiene aplicación en otros sistemas electromagnéticos.
De manera confusa, el vector de Poynting a veces se denomina flujo de potencia, que es un ejemplo del primer uso de flujo, mencionado anteriormente.[16] Tiene unidades de vatio por metro cuadrado (W/m2).
Unidades de radiometría del SI
[editar]| Magnitud | Unidad | Dimensión | Notas | ||
|---|---|---|---|---|---|
| Nombre | Símbolo[17] | Nombre | Símbolo | ||
| Energía radiante | Qe[18] | julio | J | M⋅L2⋅T−2 | Energía de la radiación electromagnética. |
| Densidad de energía radiante | we | julio por metro cúbico | J/m3 | M⋅L−1⋅T−2 | Energía radiante por unidad de volumen. |
| Flujo radiante | Φe[18] | vatio | W = J/s | M⋅L2⋅T−3 | Energía radiante emitida, reflejada, transmitida o recibida, por unidad de tiempo. A esto a veces también se le llama "potencia radiante", y se llama luminosidad en astronomía. |
| Flujo espectral | Φe,ν[19] | vatio por hercio | W/Hz | M⋅L2⋅T−2 | Flujo radiante por unidad de frecuencia o longitud de onda. Este último se mide comúnmente en W⋅nm−1. |
| Φe,λ[20] | vatio por metro | W/m | M⋅L⋅T−3 | ||
| Intensidad radiante | Ie,Ω[21] | vatio por estereorradián | W/sr | M⋅L2⋅T−3 | Flujo radiante emitido, reflejado, transmitido o recibido, por unidad de ángulo sólido. Es una cantidad "direccional". |
| Intensidad espectral | Ie,Ω,ν[19] | vatio por estereorradián por hercio | W⋅sr−1⋅Hz−1 | M⋅L2⋅T−2 | Intensidad radiante por unidad de frecuencia o longitud de onda. Este último se mide comúnmente en W⋅sr−1⋅nm−1. Es una magnitud direccional. |
| Ie,Ω,λ[20] | vatio por estereorradián por metro | W⋅sr−1⋅m−1 | M⋅L⋅T−3 | ||
| Radiancia | Le,Ω[21] | vatio por estereorradián por metro cuadrado | W⋅sr−1⋅m−2 | M⋅T−3 | Flujo radiante emitido, reflejado, transmitido o recibido por una superficie, por unidad de ángulo sólido por unidad de área proyectada. Es una cantidad "direccional", a la que a veces también se le llama confusamente "intensidad". |
| Radiancia espectral Intensidad específica |
Le,Ω,ν[19] | vatio por estereorradián por metro cuadrado por hercio | W⋅sr−1⋅m−2⋅Hz−1 | M⋅T−2 | Resplandor de una superficie por unidad de frecuencia o longitud de onda. Este último se mide comúnmente en W⋅sr−1⋅m−2⋅nm−1. Es una cantidad "direccional", a la que a veces también se le llama confusamente "intensidad espectral". |
| Le,Ω,λ[20] | vatio por estereorradián por metro cuadrado, por metro | W⋅sr−1⋅m−3 | M⋅L−1⋅T−3 | ||
| Irradiancia Densidad de flujo |
Ee[18] | vatio por metro cuadrado | W/m2 | M⋅T−3 | Flujo radiante recibido por una superficie por unidad de área. A esto a veces también se le llama confusamente "intensidad". |
| Irradiancia espectral Densidad de flujo espectral |
Ee,ν[19] | vatio por metro cuadrado por hercio | W⋅m−2⋅Hz−1 | M⋅T−2 | Irradiancia de una superficie por unidad de frecuencia o longitud de onda. A esto a veces también se le llama confusamente "intensidad espectral". Las unidades de densidad de flujo espectral que no pertenecen al SI incluyen jansky (unidad) ((1 Jy = 10−26 W⋅m−2⋅Hz− 1)) y unidad de flujo solar ((1 sfu = 10−22 W⋅m−2⋅Hz−1 = 104 Jy)). |
| Ee,λ[20] | vatio por metro cuadrado, por metro | W/m3 | M⋅L−1⋅T−3 | ||
| Radiosidad | Je[18] | vatio por metro cuadrado | W/m2 | M⋅T−3 | Flujo radiante que sale (emitido, reflejado y transmitido por) una superficie por unidad de área. A esto a veces también se le llama confusamente "intensidad". |
| Radiosidad espectral | Je,ν[19] | vatio por metro cuadrado por hercio | W⋅m−2⋅Hz−1 | M⋅T−2 | Radiosidad de una superficie por unidad de frecuencia o longitud de onda. Este último se mide comúnmente en W⋅m−2⋅nm−1. A esto a veces también se le llama confusamente "intensidad espectral". |
| Je,λ[20] | vatio por metro cuadrado, por metro | W/m3 | M⋅L−1⋅T−3 | ||
| Salida radiante | Me[18] | vatio por metro cuadrado | W/m2 | M⋅T−3 | Flujo radiante emitido por una superficie por unidad de área. Este es el componente emitido de la radiosidad. "Emitancia radiante" es un término antiguo para esta cantidad. A esto a veces también se le llama confusamente "intensidad". |
| Salida espectral | Me,ν[19] | vatio por metro cuadrado por hercio | W⋅m−2⋅Hz−1 | M⋅T−2 | Exitancia radiante de una superficie por unidad de frecuencia o longitud de onda. Este último se mide comúnmente en W⋅m−2⋅nm−1. "Emitancia espectral" es un término antiguo para esta cantidad. A esto a veces también se le llama confusamente "intensidad espectral". |
| Me,λ[20] | vatio por metro cuadrado, por metro | W/m3 | M⋅L−1⋅T−3 | ||
| Exposición radiante | He | julio por metro cuadrado | J/m2 | M⋅T−2 | Energía radiante recibida por una superficie por unidad de área, o equivalentemente irradiancia de una superficie integrada a lo largo del tiempo de irradiación. A esto a veces también se le llama "fluencia radiante". |
| Exposición espectral | He,ν[20] | julio por metro cuadrado por hercio | J⋅m−2⋅Hz−1 | M⋅T−1 | Exposición radiante de una superficie por unidad de frecuencia o longitud de onda. Este último se mide comúnmente en J⋅m−2⋅nm−1. A esto a veces también se le llama "fluencia espectral". |
| He,λ[20] | julio por metro cuadrado, por metro | J/m3 | M⋅L−1⋅T−2 | ||
| Véase también: Sistema Internacional de Unidades, Radiometría y Fotometría | |||||
Véase también
[editar]- Magnitud AB
- Generador de compresión de flujo bombeado explosivamente
- Covarianza de remolinos (también conocida como correlación de remolinos, flujo de remolinos)
- Instalación de Pruebas de Flujo Rápido
- Fluencia (flujo de primer tipo para haces de partículas)
- Fluidodinámica
- Huella de flujo
- Fijación de flujo
- Cuantificación del flujo magnético
- Ley de Gauss
- Ley de la inversa del cuadrado
- Jansky (unidad) (unidad de densidad de flujo espectral no perteneciente al SI)
- Calor latente
- Flujo luminoso
- Flujo magnético
- Cuantificación del flujo magnético
- Flujo de neutrones
- Vector de Poynting
- Teorema de Poynting
- Flujo radiante
- Cuanto rápido de flujo único
- Potencia acústica
- Flujo volumétrico (flujo de primer tipo para fluidos)
- Caudal volumétrico (flujo de segundo tipo para fluidos)
Referencias
[editar]- ↑ Purcell, p. 22-26
- ↑ Weekley, Ernest (1967). An Etymological Dictionary of Modern English. Courier Dover Publications. p. 581. ISBN 0-486-21873-2.
- ↑ Herivel, John (1975). Joseph Fourier : the man and the physicist. Oxford: Clarendon Press. pp. 181–191. ISBN 0198581491.
- ↑ Fourier, Joseph (1822). Théorie analytique de la chaleur (en francés). Paris: Firmin Didot Père et Fils. OCLC 2688081.
- ↑ a b c Maxwell, James Clerk (1892). Treatise on Electricity and Magnetism. ISBN 0-486-60636-8.
- ↑ Bird, R. Byron; Stewart, Warren E.; Lightfoot, Edwin N. (1960). Transport Phenomena. Wiley. ISBN 0-471-07392-X.
- ↑ a b P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (2nd edición). John Murray. ISBN 0-7195-3382-1.
- ↑ Carslaw, H.S.; Jaeger, J.C. (1959). Conduction of Heat in Solids (Second edición). Oxford University Press. ISBN 0-19-853303-9.
- ↑ Welty; Wicks, Wilson and Rorrer (2001). Fundamentals of Momentum, Heat, and Mass Transfer (4th edición). Wiley. ISBN 0-471-38149-7.
- ↑ D. McMahon (2006). Quantum Mechanics Demystified. Mc Graw Hill. ISBN 0-07-145546-9.
- ↑ Sakurai, J. J. (1967). Advanced Quantum Mechanics. Addison Wesley. ISBN 0-201-06710-2.
- ↑ M.R. Spiegel; S. Lipcshutz; D. Spellman (2009). Vector Analysis. Schaum's Outlines (2nd edición). McGraw Hill. p. 100. ISBN 978-0-07-161545-7.
- ↑ a b I.S. Grant; W.R. Phillips (2008). Electromagnetism. Manchester Physics (2nd edición). John Wiley & Sons. ISBN 978-0-471-92712-9.
- ↑ a b c D.J. Griffiths (2007). Introduction to Electrodynamics (3rd edición). Pearson Education, Dorling Kindersley. ISBN 978-81-7758-293-2.
- ↑ The Feynman Lectures on Physics Vol. II Ch. 4: Electrostatics
- ↑ Wangsness, Roald K. (1986). Electromagnetic Fields (2nd edición). Wiley. ISBN 0-471-81186-6. p.357
- ↑ Las organizaciones de estándares recomiendan que las magnitudes radiométricas se denoten con el sufijo e (de energético) para evitar confusión con cantidades fotométricas o fotónicas.
- ↑ a b c d e A veces se ven símbolos alternativos: W o E para energía radiante, P o F para flujo radiante, I para irradiancia, W para salida radiante.
- ↑ a b c d e f Las magnitudes espectrales dadas por unidad de frecuencia se denotan con el sufijo "ν" (letra griega nu, que no debe confundirse con la letra "v", que indica una magnitud fotométrica.
- ↑ a b c d e f g h Las cantidades espectrales dadas por unidad de longitud de onda se denotan con el sufijo "λ".
- ↑ a b Las cantidades direccionales se indican con el sufijo "Ω".
Bibliografía
[editar]- Browne, Michael, PhD (2010). Physics for Engineering and Science, 2nd Edition.. Schaum Outlines. New York, Toronto: McGraw-Hill Publishing. ISBN 978-0-0716-1399-6.
- Purcell, Edward, PhD (2013). Electricity and Magnetism, 3rd Edition. Cambridge, UK: Cambridge University Press. ISBN 978110-7014022.
Lectura adicional
[editar]- Stauffer, P.H. (2006). «Flux Flummoxed: A Proposal for Consistent Usage». Ground Water 44 (2): 125-128. Bibcode:2006GrWat..44..125S. PMID 16556188. S2CID 21812226. doi:10.1111/j.1745-6584.2006.00197.x.
Enlaces externos
[editar] Portal:Matemática. Contenido relacionado con Matemática.
Portal:Matemática. Contenido relacionado con Matemática.






























