Curva de indiferencia

En microeconomía las curvas de indiferencia (también llamadas curvas de preferencia) son combinaciones de bienes, representadas como conjuntos de puntos en el espacio, para los cuales la satisfacción de un consumidor es idéntica. Esto quiere decir que para todos los puntos pertenecientes a una misma curva, el consumidor no tiene preferencia sobre una combinación u otra. La satisfacción del consumidor se caracteriza mediante la función de utilidad, donde las variables son las cantidades de cada bien, representadas por el valor sobre cada eje.[1]
Las preferencias del consumidor le permiten elegir entre diferentes canastas de consumo. Si se ofrece a un consumidor dos canastas diferentes, elegirá la que mejor satisface sus gustos. Si ambas satisfacen sus gustos en igual medida, se dice que el consumidor es «indiferente» entre las dos canastas. Existen discrepancias entre autores sobre si la continuidad, derivabilidad y convexidad de dichas curvas están garantizadas y ello tiene fuertes implicaciones en la discusión sobre la existencia o no de puntos de equilibrio. Desde un punto de vista matemático la discusión implica el axioma de elección.[2]

La representación gráfica más habitual presenta dos bienes alternativos X e Y (Figura 1) entre los cuales el consumidor puede elegir. Los puntos de cada curva representan las combinaciones de bienes X e Y que proporcionan la misma utilidad al consumidor.
Historia[editar]
La teoría de las curvas de indiferencia fue desarrollada por Francis Edgeworth en su libro Mathematical Psychics: an Essay on the Application of Mathematics to the Moral Sciences, 1881,[3] Vilfredo Pareto las dibujó por primera vez en su libro "Manuale di economia politica con una introduzione alla scienza sociale", 1906.[4] La teoría se deriva de la teoría de la utilidad ordinal, donde se presupone que los individuos pueden clasificar cualquier combinación de bienes por orden de preferencia, siendo el origen de esta los trabajos de William Stanley Jevons.
Mapa de curvas[editar]
Cada combinación de bienes ofrece un determinado nivel de utilidad, por lo que pasan curvas de indiferencia por todos los puntos del plano. Las curvas de indiferencia son de esta manera similares a las curvas de nivel de un mapa, que representan líneas de la misma altitud. Existen infinitas curvas de indiferencia en un plano.[5]
La representación gráfica que muestra el conjunto de curvas de indiferencia para un consumidor se denomina mapa de indiferencia. Los puntos que muestran diferentes niveles de utilidad están asociados con distintas curvas de indiferencia. Una curva de indiferencia describe las preferencias personales, por lo que puede variar entre individuos. El mapa de indiferencia muestra así las preferencias del consumidor ordenadas, el salto de una curva a otra conlleva un salto en la utilidad del individuo.
Propiedades de las curvas de indiferencia[editar]
Las curvas de indiferencia representan las preferencias del consumidor y de forma genérica se pueden sacar conclusiones sobre ellas que son trasladables a las propiedades de las curvas de indiferencia, son por tanto las reglas o propiedades que rigen la ordenación del mapa de curvas de indiferencia de un individuo. La teoría del consumidor se basa en preferencias regulares de los consumidores para que los equilibrios enunciados sean válidos, por tanto las preferencias y por tanto las curvas de indiferencia han de cumplir una serie requisitos para estudiar el equilibrio del consumidor:
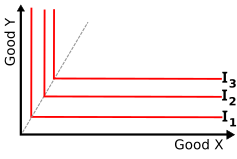
- Se prefieren las curvas más alejadas del origen. Dado el axioma de insaciabilidad, los consumidores prefieren combinaciones con una cantidad mayor de bienes. En la figura 1, se muestra un mapa de indiferencia compuesto por tres curvas. La que está situada más a la derecha y más arriba (I3) representa un consumo de mayor que la situada más a la izquierda y más abajo (I1), por tanto, el consumidor prefiere la curva de indiferencia más alta (I3) a la más baja (I1).[6]
- Son decrecientes. De acuerdo al principio expuesto anteriormente, las curvas de indiferencia deben ser decrecientes, es decir, tienen pendiente negativa. Una disminución en el consumo de un bien se compensa con un incremento en el consumo del otro bien para mantener la misma satisfacción. También se podría expresar de forma que el incremento del consumo de un bien (X) no produce un incremento de la satisfacción total del individuo si se compensa con una disminución del consumo del otro bien (Y). La pendiente de una curva de indiferencia (relación marginal de sustitución) refleja la tasa a la cual el consumidor está dispuesto a sustituir un bien por el otro. En la mayoría de los casos, al consumidor le agradan ambos bienes. Por consiguiente, si la cantidad de un bien se reduce, la cantidad del otro bien se debe aumentar para que el consumidor se sienta igualmente satisfecho. Por esta razón, la mayoría de las curvas de indiferencia tiene pendiente negativa. Como excepción, solo las curvas de indiferencia correspondientes a bienes cuyo consumo produce un rechazo, serían crecientes.[7]
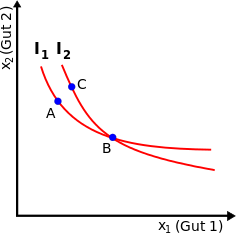
- Las curvas de indiferencia no se cruzan. A partir del carácter transitivo de las preferencias se deduce que pasa una única curva de indiferencia por cada punto del espacio. Si dos curvas de indiferencia se cruzasen, como en el punto B de la Figura 3, entonces, debido a que el punto B se encuentra en la misma curva de indiferencia que el punto A, los dos puntos producirían la misma satisfacción al consumidor. Además, debido a que el punto B se encuentra en la misma curva de indiferencia que el punto C, estos dos puntos también otorgarían la misma utilidad. Pero estas conclusiones implican que los puntos A y C también harían al consumidor igualmente feliz, aun cuando el punto C tiene más de ambos bienes. Esto contradice el supuesto de que el consumidor siempre prefiere más de ambos bienes que menos. Por esta razón, las curvas de indiferencia no se pueden cruzar.[7]
- Son curvas convexas hacia el origen. Esto significa que se valora más un bien cuanto mayor es su escasez. Cuando se dispone en abundancia de un bien, el consumidor está dispuesto a prescindir de una unidad a cambio de poca cantidad del bien alternativo. Sin embargo cuando renuncia a un bien escaso, solo mantiene su nivel de utilidad si cada unidad renunciada se compensa con cantidades crecientes del otro bien. La pendiente de una curva de indiferencia es la tasa marginal de sustitución, entendida como la relación de intercambio entre bienes dispuesta por un consumidor . La tasa marginal de sustitución depende usualmente de la cantidad de cada bien que el individuo se encuentra consumiendo. En particular, debido a que las personas están más dispuestas a intercambiar los bienes que poseen en abundancia y menos dispuestas a intercambiar aquellos bienes de los que tienen poco, las curvas de indiferencia son convexas al origen.
Aplicaciones[editar]
Las curvas de indiferencia junto con el presupuesto que dispone el consumidor para gastar (recta de balance) son los elementos fundamentales para determinar el punto de equilibrio de un consumidor y con él deducir su curva de demanda, definida como el conjunto de puntos que potencialmente pueden ser de equilibrio. El conjunto de puntos de equilibrio de que se derive la curva de demanda se llama la Curva precio-consumo. Para que las conclusiones alcanzadas en el equilibrio del consumidor sean correctas, es necesario que las preferencias de los consumidores sean regulares y por tanto las curvas de indiferencia cumplan las restricciones exigidas por el modelo (continuidad, derivabilidad, convexidad, utilidad marginal decreciente en ambos bienes, no sustituibilidad perfecta, entre otros).[8][9]
Ejemplo de curvas de indiferencia[editar]
En la figura 1, el consumidor preferirá I3 en vez de I2, y también preferirá I2 mejor que I1, pero no informa donde se colocará el consumidor dentro de la curva. La pendiente de una curva de indiferencia (en valor absoluto), conocido por los economistas como relación marginal de sustitución, mide la relación en la que el consumidor está dispuesto a sustituir un bien por el otro. Para la mayoría de los bienes la relación marginal de sustitución no es constante, así que sus curvas de indiferencia son curvas. Las curvas son convexas al origen, mostrando el efecto sustitución negativo.
Sustitutivos perfectos[editar]
Si los bienes son bienes sustitutivos perfectos, las curvas de indiferencias serán rectas paralelas, con una pendiente constante. La relación marginal de sustitución será constante a lo largo de toda la curva. Un ejemplo de función de utilidad que está asociada con las curvas de indiferencia como éstas podría ser: .
Complementarios perfectos[editar]
Si los bienes son perfectamente complementarios las curvas de indiferencia tendrán forma de "L". Un ejemplo típico de bienes complementarios perfectos sería zapatos del pie izquierdo y zapatos del pie derecho. A un consumidor le es indiferente que se incremente el número de zapatos del pie derecho mientras no lo hagan también los zapatos del pie izquierdo. La característica más importante de estos bienes es que el consumidor prefiere consumirlos en proporciones fijas. Un ejemplo de función como el descrito sería: .
Las diversas formas de las curvas implican respuestas diferentes a un cambio en precio como muestra el análisis de la demanda dentro de la teoría del consumidor.
Véase también[editar]
Bibliografía[editar]
- Bruce R. Beattie and Jeffrey T. LaFrance, “The Law of Demand versus Diminishing Marginal Utility” (2006). Review of Agricultural Economics. 28 (2), pp. 263-271.
- Frank, Robert H. (2008). Microeconomía y conducta (7.ª edición). McGraw-Hill. ISBN 84-7615-840-8. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- Volker Böhm and Hans Haller (1987). "Demand theory," The New Palgrave: A Dictionary of Economics, v. 1, pp. 785-92.
- John Geanakoplis (1987). "Arrow-Debreu model of general equilibrium," The New Palgrave: A Dictionary of Economics, v. 1, pp. 116-24.
- Hal R. Varian (2010) "Microeconomía intermedia". 8va. Ed. Antoni Bosch, pp. 35-46.
- Mankiw, Gregory (2012) "Principios de Economía". 6ta. Ed. Cengage learning, pp. 439-451.
Referencias[editar]
- ↑ Komlos, John (24 de julio de 2014). «Sticky prices and behavioural indifference curves». VoxEU.org. Consultado el 10 de agosto de 2021.
- ↑ Varian, Hal R. (1992). Microeconomic analysis (Tercera edición). Norton. p. 95-108. ISBN 0-393-09036-1. OCLC 3706403. Consultado el 10 de agosto de 2021.
- ↑ http://onlinebooks.library.upenn.edu/webbin/book/lookupid?key=olbp34052
- ↑ http://archive.org/details/manualedieconomi00pareuoft
- ↑ Nicholson, Walter (2004). «3». Teoría microeconómica. Principios básicos y ampliaciones. Paraninfo. ISBN 9788497322492.
- ↑ Frank, Robert H. (D.L. 1992). Microeconomía y conducta. McGraw-Hill. ISBN 84-7615-840-8. OCLC 433444783. Consultado el 10 de agosto de 2021.
- ↑ a b Frank 2008: p.72
- ↑ Lipsey, Richard G. (1975). An introduction to positive economics (4th ed edición). Weidenfeld and Nicolson. ISBN 0-297-76899-9. OCLC 1514644. Consultado el 10 de agosto de 2021.
- ↑ Varian, Hal R. (2003). Intermediate microeconomics : a modern approach (6. ed., internat. student ed edición). Norton. ISBN 0-393-92671-0. OCLC 254988619. Consultado el 10 de agosto de 2021.
Enlaces externos[editar]
- Maximización de utilidad. Policonomics