Curva de Lorenz

La curva de Lorenz es una representación gráfica utilizada frecuentemente para plasmar la distribución relativa de una variable en un dominio determinado. El dominio puede ser el conjunto de hogares o personas de una región o país, por ejemplo. La variable cuya distribución se estudia puede ser el ingreso de los hogares o las personas. Utilizando como ejemplo estas variables, la curva se trazaría considerando en el eje horizontal el porcentaje acumulado de personas u hogares del dominio en cuestión y en el eje vertical el porcentaje acumulado del ingreso. Su autoría es de Max Otto Lorenz en 1905.
Cada punto de la curva se lee como porcentaje acumulativo de los hogares o las personas. La curva parte del origen (0,0) y termina en el punto (100,100). Si el ingreso estuviera distribuido de manera perfectamente equitativa, la curva coincidiría con la línea de 45 grados que pasa por el origen (por ejemplo el 30% de los hogares o de la población percibe el 30% del ingreso). Si existiera desigualdad perfecta, o sea, si un hogar o persona poseyera todo el ingreso, la curva coincidiría con el eje horizontal hasta el punto (100,0) donde saltaría el punto (100,100). En general la curva se encuentra en una situación intermedia entre estos dos extremos.
Curva de Lorenz y desigualdad[editar]
Si una curva de Lorenz se encuentra siempre por encima de otra (por lo tanto, está más cerca de la línea de 45 grados que la otra), entonces podemos decir, sin ambigüedad, que la primera exhibe menor desigualdad que la segunda. Esta comparación gráfica entre distribuciones de distintos dominios geográficos o temporales es el principal empleo de las curvas de Lorenz. El indicador gráfico de bienestar más usado es la Curva de Lorenz Generalizada (CLG), que es una derivación de la curva de Lorenz habitual. La CLG sólo se diferencia de la de Lorenz en que en la escala vertical no se representan las cantidades relativas acumuladas sino las cantidades acumuladas (no relativas) divididas por el número N de elementos de la población. La lógica pretendida es representar qué cantidad absoluta corresponde a cada porcentaje de individuos. Para clarificar este aspecto, supóngase que la curva de Lorenz normal de una población nos dice que el 50% de los menos ricos poseen el 25% de la riqueza total. Se puede comprender que es muy diferente la situación de bienestar de este 50% de la población según si la riqueza total es muy pequeña o muy grande. Es obvio que es peor poseer el 50% de una cantidad pequeña que poseer el 25% de una cantidad mucho mayor. El dividir las cantidades acumuladas por el total de elementos N es necesario para poder comparar riquezas entre poblaciones distintas que tengan un número diferente de elementos: no es lo mismo una riqueza total de 1.000.000€ en un conjunto de 10 personas que esa misma riqueza total en un conjunto formado por 1.000 personas.
Ecuación de la curva de Lorenz[editar]
Si se conoce la distribución de la renta como densidad de probabilidad para cada valor de renta, la curva de Lorenz puede encontrarse analíticamente en función de ésta. La proporción de personas o unidades familiares con una renta inferior a un nivel de renta r viene dada por:
(1)
Mientras que la proporción de renta acumulada por las personas con rentas iguales o inferiores a r viene dada por:
(2)
Donde es la renta media. Las ecuaciones () y () constituyen juntas las ecuaciones paramétricas de la curva en función del parámetro r.
Propiedades[editar]
La curva de Lorenz tiene pendiente positiva en todos sus puntos como se deduce de la siguiente relación:
(3)
En el punto inicial la pendiente será nula (aun en el caso el límite anterior sigue siendo válido, pero en el resto de puntos será estrictamente positiva.
Además la curva de Lorenz es convexa ya que su derivada segunda siempre es positiva:
(4)
Ejemplo 1[editar]
En esta sección calculamos la curva de Lorenz y el índice de Gini para una distribución de renta exponencial. Aunque ésta no parece una distribución adecuada para la renta nacional de ningún país, la sencillez de las expresiones obtenidas permite entender de modo sencillo la aplicación de las ecuaciones () a (). Para un país con una renta nacional media con una distribución exponencial la densidad de probabilidad de la distribución será:
Esta expresión permite calcular la proporción de personas por debajo de una cierta renta y la renta acumulada de ese grupo de personas fácilmente:
Despejando de la primera ecuación y substituyendo el resultado en la segunda se obtiene la curva de Lorenz explícitamente:
El índice de Gini se puede calcular simplemente como:
Este es el valor exacto. Cuando para calcular este valor en lugar de una distribución continua se usa un cálculo aproximado por decilas en cambio resulta sólo .
Ejemplo 2[editar]
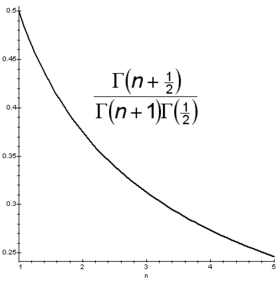
Una aproximación más verosimil para la renta nacional es usar en lugar de una simple distribución exponencial, una distribución gamma:
Donde el parámetro está relacionado con la renta media mediante . Después de una cierta cantidad de álgebra trivial pero engorrosa puede encontrarse que la proporción de personas por debajo de una cierta renta y la renta acumulada de ese grupo de personas vienen dadas por:
Donde:
En este caso no es posible despejar explícitamente de la primera ecuación. Aunque puede calcularse el índice de Gini mediante la expresión (para entero):
En este caso el coeficiente de Gini tampoco depende de la renta media. Dado que el índice de Gini de la mayor parte de países está entre 0,50 y 0,25 la distribución gamma anterior puede usarse de manera aproximada para reproducir la distribución real de la renta.
Véase también[editar]
Enlaces externos[editar]
- La distribución de la renta, la curva de Lorenz y el índice de Gini
- Índice de Gini por países
- (en inglés) A complete handhout (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última). about the Lorenz curve including various applications, including an Excel spreadsheet graphing Lorenz curves and calculating Gini coefficients as well as coefficients of variation.
























