Comportamiento colectivo de los animales

El comportamiento colectivo de los animales describe el comportamiento coordinado de grandes grupos de animales similares y las propiedades emergentes de estos grupos. Entre las facetas que comprende este tópico se incluyen los costes y beneficios asociados con la pertenencia al grupo, la transferencia de información en el grupo, el proceso de toma de decisiones del grupo, y la locomoción y sincronización del grupo. El estudio de los principios asociados al comportamiento colectivo de los animales tiene relevancia para el tratamiento de problemas de ingeniería humana mediante la filosofía de la biomimética. Por ejemplo, determinar la reglas mediante las cuales un animal individual navega con relación a sus vecinos en un grupo puede conducir a avances en la disposición y control de grupos de micro-robots nadadores o voladores tales como UAVs (Vehículos aéreos no tripulados).
Ejemplos[editar]
Entre los ejemplos de comportamiento colectivo de animales se encuentran:
- Bandadas de aves
- Manadas de ungulados
- Cardumen de peces
- Enjambres de kril antártico
- Grupos de delfines
- Bandadas de langostas
- Construcción de hormigueros por las hormigas
Funciones propuestas[editar]
Se han propuesto muchas funciones de agregaciones de animales. Estas funciones propuestas pueden ser agrupadas en las siguientes cuatro categorías: sociales y genéticas, anti-depredadores, optimización de la alimentación, y aumento de la eficiencia de locomoción.
Interacción social[editar]
Es posible observar el apoyo a las funciones sociales y genéticas de las agregaciones, especialmente aquellas formadas por peces, en varios aspectos de su comportamiento. Por ejemplo, ciertos experimentos han mostrado que peces individuales extraídos de un cardumen pueden presentar un ritmo respiratorio más elevado que aquellos que permanecen en el cardumen. Este efecto puede ser atribuido al estrés, por lo que el efecto de estar en compañía de conespecíficos por lo tanto parece tener un efecto tranquilizador y ser una poderosa motivación social para permanecer en una agregación.[1] Por ejemplo ejemplares de arenque, se agitan mucho si son aislados de sus conespecíficos.[2] Se ha propuesto también que los cardúmenes cumplen también con una función reproductiva ya que permiten aumentar el acceso a los machos.
Protección ante depredadores[editar]

Se han propuesto varias funciones anti-depredadores de las agregaciones de animales. Un posible método por medio del cual cardúmenes de peces o bandadas de aves pueden combatir a los depredadores es el ‘efecto de confusión del depredador’ propuesto y demostrado por Milinksi y Heller (1978).[3] Esta teoría se basa en la idea de que es difícil para los depredadores elegir una presa individual de entre grandes grupos a causa de que los numerosos objetivos móviles sobrecargan el canal visual del depredador.
Un segundo efecto potencial anti-depredador de las agregaciones de animales es la hipótesis de ‘muchos ojos’. Esta teoría establece que en la medida que el tamaño del grupo aumenta, la tarea de vigilar el entorno para detectar depredadores puede ser compartida entre numerosos individuos. No solo que esta colaboración en masa presumiblemente provee un nivel de vigilancia más elevado, sino que además permitiría más tiempo para alimentación individual.[4][5]
Una tercera hipótesis del efecto anti-depredatorio de la agregación de animales es el efecto de ‘dilución del encuentro’. Por ejemplo Hamilton, propuso que la agregación de animales se debía a una forma “egoísta” de evitar a un depredador y por lo tanto era una forma de búsqueda de cobertura.[6] Otra formulación de la teoría fue presentada por Turner y Pitcher y fue interpretada como una combinación de probabilidades de detección y ataque.[7] En cuanto a la componente de detección de la teoría, se propuso que las presas potenciales se podrían beneficiar viviendo juntas dado que es menos probable que un depredador intente suerte con un grupo que con una distribución dispersa. En cuanto al componente de ataque, se propuso que un depredador que ataca es menos probable que coma a un animal en particular cuando se encuentran presentes un número mayor de animales. En resumen, un individuo posee ventajas cuanto mayor es el grupo en el cual se encuentra, suponiendo que las probabilidades de detección y ataque no aumentan en forma desproporcionada con el tamaño del grupo.[8]
Mejor forrajeo[editar]
Un tercer beneficio propuesto como consecuencia de la agregación de animales en grupos es el de mejor forrajeo. Esta habilidad fue demostrada por Pitcher et Al. en su estudio sobre el comportamiento de alimentación en cardúmenes de cypriniformes.[9] En este estudio, se determinó el tiempo que le requería a grupos de pececillos de la familia Gerreidae y peces dorados (Carassius spp.) encontrar un trozo de alimento. Se variaron la cantidad de individuos que componían los grupos, y fue posible determinar una disminución estadísticamente significativa en el tiempo requerido por los grupos mayores para encontrar el alimento respecto al tiempo requerido por los grupos más pequeños. Evidencia adicional sobre este mejoramiento de la capacidad de alimentación en cardúmenes se observa en la estructura de los cardúmenes de peces depredadores. Partridge et al. analizaron la estructura de cardúmenes de atún del Atlántico (Thunnus) a partir de fotografías aéreas y descubrieron que el cardumen tomaba una forma parabólica, un elemento que parece indicar un comportamiento de caza cooperativa en esta especie (Partridge et al., 1983).[10]
Aumento de la eficiencia de locomoción[editar]
Esta teoría establece que los grupos de animales que se desplazan en un medio fluido podrían ahorrar energía cuando nadan o vuelan juntos, en forma similar a lo que hacen los ciclistas cuando viajan en pelotón y aprovechan las fuerzas dinámicas que se generan (succión). Se piensa que los gansos que vuelan en una formación en "V" también ahorran energía al volar ya que aprovechan el empuje generado por los vórtices del extremo alar generado por el animal que vuela delante de ellos en la formación. También se ha demostrado que los patos ahorran energía al nadar en una formación en fila.[11] Aumentos de eficiencia en grupos que se desplazan nadando ha sido también propuesto para los cardúmenes de peces y kril antártico.
Estructura de grupo[editar]
Ha sido difícil estudiar la estructura de grandes grupos de animales a causa de la gran cantidad de individuos que participan. Por lo tanto el enfoque experimental a menudo es complementado con el modelado matemático de agregaciones de animales.
Enfoque experimental[editar]
Los experimentos que investigan la estructura de grandes agregaciones de animales intentan determinar la posición en un espacio de tres dimensiones de cada animal en función del tiempo. Es importante conocer la estructura interna del grupo porque dicha estructura puede estar relacionada con la motivaciones que pueden promover el agrupamiento de los animales. Para poder determinar dicha estructura es preciso utilizar varias cámaras ubicadas en el volumen del espacio a estudiar, una técnica denominada estereofotogrametría. Cuando el volumen que se estudia es ocupado por cientos de miles de animales, se vuelve difícil identificar a cada uno de ellos. Además, los animales se pueden solapar en la imagen fotográfica, un problema denominado oclusión. Una vez que se logra determinar la ubicación de cada animal a lo largo del tiempo, es posible extraer una serie de parámetros que describen al grupo de animales.
Estos parámetros son:
- Densidad: La densidad de una agregación de animales es el número de animales dividido por el volumen (o área) que ocupa la agregación. La densidad puede no ser constante en todo el grupo. Por ejemplo, se ha determinado que las bandadas de estorninos poseen una mayor densidad en los bordes de la bandada que en su zona central, una característica que se sospecha puede estar relacionada con la defensa ante depredadores.[12]
- Polaridad: La polaridad del grupo describe si los animales del grupo se encuentran orientados en la misma dirección o no. Para determinar este parámetro, se determina la orientación promedio de todos los animales que componen el grupo. Para cada animal se evalúa la diferencia angular entre su orientación y la orientación del grupo. La polaridad del grupo se obtiene como el promedio de estas diferencias (Viscido 2004).[13]
- Distancia al vecino más próximo: La distancia al vecino más próximo es la distancia entre el centroide de un animal (animal bajo análisis o animal en foco) y el centroide del animal más cercano al animal bajo análisis. Es posible obtener este parámetro para cada animal en una agregación y calcular su promedio. Se debe tener cuidado al contabilizar a los animales que se encuentran en los bordes de una agregación de animales. Estos animales no poseen vecino en una dirección.
- Posición del vecino más próximo: En un sistema de coordenadas polares, la posición del vecino más próximo es descrita por el ángulo y distancia a la que se encuentra el vecino más próximo con respecto al individuo bajo análisis.
- Fracción de compactación: la fracción de compactación (en inglés: packing fraction) es un parámetro tomado de la física que define la organización (o estado: sólido, líquido, o gaseoso) de grupos de animales en tres dimensiones. Es una medida alternativa a la densidad. En este parámetro, la agregación es idealizada como un ensamble de esferas sólidas, en el que cada animal se encuentra en el centro de una esfera. La fracción de compactación se define como la relación entre el volumen total ocupado por todas las esferas individuales dividido por el volumen global de la agregación (Cavagna 2008). El rango de valores fluctúa entre cero y uno, donde una fracción de compactación pequeña es indicativa de un sistema diluido tal como un gas. Cavagna encontró que la fracción de compactación para grupos de estorninos era 0.012.[14]
- Densidad condicional integrada: Este parámetro mide la densidad en varias escalas de longitud y por lo tanto describe la homogeneidad de la densidad a través de un grupo de animales.[14]
- Función de distribución de pares: Por lo general este parámetro es utilizado en el ámbito de la física para caracterizar el grado de orden espacial en un sistema de partículas. También describe la densidad, pero esta medida describe la densidad a cierta distancia de un punto determinado. Cavagna et al. encontraron que las bandadas de estorninos presentaban más estructura que un gas pero menos que un líquido.[14]
Modelado[editar]
Los modelos matemáticos más simples de agregaciones de animales generalmente requieren que los animales individuales que deben obedecer tres reglas:
- Moverse en la misma dirección que su vecino
- Permanecer cerca de sus vecinos
- Evitar choques con sus vecinos
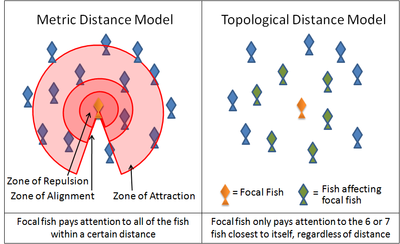
Un ejemplo de este tipo de simulaciones es el programa Boids creado por Craig Reynolds en 1986. Otro es el modelo de Partícula Autopropulsada. Numerosos modelos actuales utilizan variaciones de estas reglas. Por ejemplo, muchos modelos implementan estas reglas mediante una serie de zonas en capas alrededor de cada animal. En la zona de repulsión muy próxima al animal, el animal tratar de apartarse de sus vecinos para evitar una colisión. La capa que sigue un poco más lejana constituye la de alineación, y en ella el animal focal trata de mantener su alineación respecto a la dirección de desplazamiento de sus vecinos. En la zona de atracción exterior, que se extiende tanto como alcanzan las señales que recogen sus órganos sensoriales, el animal focal trata de desplazarse hacia un vecino. La forma de estas zonas necesariamente dependen de las habilidades sensoras del animal. Por ejemplo, el campo visual de un animal no alcanza la zona detrás de su cuerpo. Por otra parte los peces, dependen tanto de la visión como de señales hidrodinámicas recogidas por su línea lateral. El kril antártico depende de su visión y de señales hidrodinámicas captadas por sus antenas.
Sin embargo estudios recientes de bandadas de estorninos han concluido, que cada ave modifica su posición en forma relativa a los seis o siete animales que se encuentran en su entorno inmediato, sin importar cuan cerca o lejos se encuentren dichos animales.[15] Por lo tanto las interacciones entre estorninos en una bandada están basadas en una regla topológica y no en una regla métrica. No se ha demostrado todavía si esta misma regla es aplicable a otros animales.
Véase también[editar]
Referencias[editar]
- ↑ Abrahams, M. and Colgan, P. Risk of predation, hydrodynamic efficiency, and their influence on school structure. Environmental Biol of Fishes 13, 3, pp 195-202, 1985.
- ↑ Partridge, B., Pitcher, T., Cullen, M., and Wilson, J. The three-dimensional structure of fish schools. Behav Ecol and Sociobiology 6:4, pp 277-288. 1980.
- ↑ Milinski, H. and Heller, R. Influence of a predator on the optimal foraging behavior of sticklebacks. Nature 275, pp642-644. 1978.
- ↑ Roberts, G. Why individual vigilance increases as group size increases. Anim Behav. 51. pp 1077-1086. 1996.
- ↑ Lima, S. Back to the basics of anti-predatory vigilance: the group-size effect. Animal Behaviour 49:1. pp 11-20. 1995.
- ↑ Hamilton, W. D. Geometry for the selfish herd. J. Theor Biology 31, pp 295-311. 1971
- ↑ Turner, G. and Pitcher, T. Attack abatement: a model for group protection by combined avoidance and dilution. American Naturalist 128:2, pp228-240. 1986.
- ↑ Krause, J., Ruxton, G., and Rubenstein, D. Is there always an influence of shoal size on predator hunting success? Journal of Fish Biology 52, pp 494-501. 1998.
- ↑ Pitcher, T., Magurran, A., and Winfield, I. Fish in larger shoals find food faster. Behav. Ecol. and Sociobiology 10:2, 1982.
- ↑ Partridge, B. Johansson, J and Kalish, J. The structure of schools of giant bluefin tuna in Cape Cod Bay. Environmental Biology of Fishes 9: 3-4. pp 253. 1983.
- ↑ Fish, F.E. Kinematics of ducklings swimming in formation: consequences of position. (1995) Journal of Experimental Zoology 273:1-11.
- ↑ M. Ballerini, N. Cabibbo, R. Candelier, A. Cavagna, E. Cisbani, I. Giardina, A. Orlandi, G. Parisi, A. Procaccini, M. Viale, and V. Zdravkovic (2008) ‘Empirical investigation of starling flocks: a benchmark study in collective animal behaviour’ Animal Behavior 76(1): 201-215.
- ↑ Viscido, S., Parrish, J., and Grunbaum, D. (2004) Individual behavior and emergent properties of fish schools: a comparison of observation and theory. Marine Ecology Progress Series 273:239-249.
- ↑ a b c Cavagna, A., Cimarelli, Giardina, Orlandi, Parisi, Procaccini, Santagati and Stefanini. (2008). New statistical tools for analyzing the structure of animal groups. Mathematical Biosciences 214:32-37.
- ↑ M. Ballerini, N. Cabibbo, R. Candelier, A. Cavagna, E. Cisbani, I. Giardina, V. Lecomte, A. Orlandi, G. Parisi, A. Procaccini, M. Viale, and V. Zdravkovic (2008) ‘Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study’ PNAS 105:1232-1237.
Bibliografía[editar]
- Camazine, S., Deneubourg, J.L., Franks, N.R., Sneyd, J., Theraulaz, G. and Bonabeau, E. (2003) Self-Organization in Biological Systems Princeton University Press, Princeton, N.J. ISBN 0-691-01211-3 (especially Chapter 11)
Enlaces externos[editar]
- Sitio web sobre el comportamiento colectivo de los animales basado en el libro de David Sumpter (2008) con este nombre
- STARFLAG project: Descripción del comportamiento de estorninos
- Center for Biologically Inspired Design, Georgia Tech
- Sitio web de investigaciones de David Sumpter
- Sitio web de investigaciones de Iain Couzin
- Sitio web de Julia Parrish, una investigadora de agregación de los animales Archivado el 26 de mayo de 2009 en Wayback Machine.
- La investigación para este artículo de Wikipedia fue llevado a cabo como parte de un curso de neuromecánica de la locomoción (APPH 6232) de la escuela Applied Physiology, Georgia Tech
