Catenaria

Una catenaria es una curva ideal que representa físicamente la curva generada por una cadena, cuerda o cable sin rigidez flexional, suspendida de sus dos extremos y sometida a un campo gravitatorio uniforme. Esta palabra proviene del latín catēnarĭus (‘propio de la cadena’). La evoluta de una tractriz es una catenaria.
Historia[editar]
La problemática de la catenaria, planteada durante el siglo XVII, consistía en determinar la forma que adoptaba una cadena o cuerda (sin rigidez flexional) dentro de un campo gravitatorio uniforme. Es decir, cuando sobre un segmento de cuerda actuaba el propio peso de la cuerda verticalmente y era sostenido simultáneamente por las tensiones en sus extremos, en direcciones tangentes a un segmento de curva en sus extremos. Los primeros físicos y matemáticos que abordaron el problema supusieron que la curva era una parábola, porque empíricamente la forma de la cuerda se parece mucho a una parábola, especialmente si se consideran longitudes pequeñas de cuerda. Pero fue Christiaan Huygens, a los 17 años, quien demostró que la curva no era realmente una parábola, sino sólo una curva parecida, aunque no encontró la ecuación de la catenaria.
La ecuación fue obtenida por Gottfried Leibniz, Christiaan Huygens y Johann Bernoulli en 1691, en respuesta al desafío planteado por Jakob Bernoulli. Huygens fue el primero en utilizar el término catenaria en una carta dirigida a Leibniz en 1690 y David Gregory escribió, ese mismo año, un tratado sobre la curva.[1]
Enfoque matemático[editar]
La condición de equilibrio de un cable sometido a su propio peso vertical lleva a un problema de equilibrio en el plano (la catenaria es siempre una curva plana si se puede despreciar la rigidez flexional del cable). De la condición de equilibrio local de cada punto se desprende la siguiente ecuación diferencial para la pendiente de la catenaria, que relaciona las tensiones en los extremos de un tramo y el peso del mismo (ver deducción de la catenaria):
(1)
Donde:
- es el peso por unidad de longitud, que se supone constante.
- la tensión horizontal que aparecerá en los extremos del cable.
La solución general viene dada por:
(2)
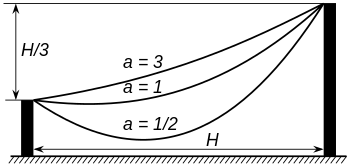
La solución de la ecuación anterior para un cable suspendido de dos puntos a la misma altura y cuyo punto mínimo es el punto (0,a) resulta ser:
es la componente horizontal de la tensión, que es constante, es la masa por unidad de longitud del hilo y es la función coseno hiperbólico. Si se desarrolla en series de Taylor la ecuación de la catenaria () se obtiene una curva cercana a una parábola:
Esto corresponde a la ecuación de una parábola más un término de cuarto orden. Por este motivo ambas gráficas son tan parecidas en el entorno de cero.

Relaciones importantes[editar]
En el caso de un cable suspendido de dos puntos a la misma altura, la longitud del arco, con el origen de arco en el mínimo es:
La inclinación (esto es, la tangente de dicha inclinación) es:
Por tanto, la tensión vertical es:
La tensión total del hilo es
con lo que sustituyendo , se tiene
Deducción de la ecuación de la catenaria[editar]

La ecuación diferencial () puede deducirse aplicando el equilibrio de fuerzas a una porción infinitesimal de catenaria. Aplicando el equilibrio de fuerzas a las fuerzas horizontales y verticales se tiene que:
Donde:
- es el ángulo formado por la catenaria y la horizontal.
- es la tensión total del cable para cada punto.
- es la masa por unidad de longitud.
La primera de las ecuaciones implica que mientras que la segunda de ellas puede escribirse escogiendo adecuadamente el origen de la longitud de arco como:
Introduciendo la relación entre la tangente del ángulo de la pendiente y la longitud de arco:
Derivando la última relación se obtiene precisamente ().
En resumen[editar]
Una cuerda pesada, flexible, inextendible y suspendida de dos puntos toma la forma de la catenaria. Esta catenaria es una curva plana cuya ecuación empleando coordenadas cartesianas (contenidas en el plano de la curva) y escogidas de manera que el eje Y coincida con el mínimo de la curva, resulta ser:
La curva es simétrica con respecto al eje y, y cerca del punto más bajo se asemeja mucho a la parábola . Esta parábola pasa en todos los puntos por debajo de la catenaria. Esta curva tiene las siguientes propiedades:
- El vértice o mínimo de la curva viene dado por .
- La longitud del arco AM es
- El área OAMP es .
- El radio de curvatura es .[2]
Generalizaciones[editar]
En lo general la ecuación de la catenaria se refiere a cadenas o cuerdas infinitamente flexibles e inextensibles. El requisito de flexibilidad infinita se refiere a que la rigidez flexional sea nula y el requisito de inextensibilidad se refiere a que la longitud de cada tramo de la misma no varíe a pesar de estar sometido a fuerzas. Obviamente en las cuerdas reales estos requisitos se cumplen sólo de forma aproximada. Para cuerdas de gran longitud, la elasticidad de la cuerda las aleja del comportamiento perfectamente inextensible. Si bien la catenaria de una cuerda inextensible es siempre una curva plana, para cables gruesos de pequeña longitud la rigidez flexional finita hace que su deformada no necesariamente esté contenida en un plano.
Aplicaciones[editar]



Dado un elemento lineal sometido solo a cargas verticales, la forma catenaria es precisamente la forma del eje baricéntrico que minimiza las tensiones. Esa propiedad puede aprovecharse para el diseño de arcos. De este modo un arco en forma de catenaria invertida es precisamente la forma en la que se evita la aparición de esfuerzos distintos de los de compresión, como son los esfuerzos cortantes o los flectores.
Por esa razón, una curva catenaria invertida es un trazado útil para un arco en la arquitectura, forma que fue aplicada, entre otros, y fundamentalmente, por Antonio Gaudí. El mismo utilizaba maquetas para el estudio de estas estructuras, para luego volcar aquella información en los planos de sus obras.
Véase también[editar]
Referencias[editar]
- ↑ John D. Barrow (2009). El salto del tigre: Las matemáticas de la vida cotidiana. Grupo Planeta (GBS). pp. 42 de 368. ISBN 9788498920161. Consultado el 1 de junio de 2021.
- ↑ Bronshtein- Semendiaev. Manual de matemáticas para ingenieros y estudiantes. Editorial Mir, Moscú. Varias impresiones
Enlaces externos[editar]
- La curva catenaria
- Índice de curvas famosas (en inglés)











![{\displaystyle y(x)\approx a\left[\left(1+{\frac {C_{2}}{a}}\right)+{\frac {1}{2}}{\frac {(x-C_{1})^{2}}{a^{2}}}\right]+O(x^{4})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6d8113d31901182ed0af63e43f91c0dfb407450)


















