Renormalización
En teoría cuántica de campos y otras áreas, la renormalización se refiere a un conjunto de técnicas usadas para obtener términos finitos en un desarrollo perturbativo. La renormalización es importante porque en teoría cuántica de campos no se conocía la manera de calcular ciertas magnitudes de otra manera que no sea una serie formal de potencias[nota 1]. El problema es que algunos de los términos de la serie pueden resultar divergentes en el límite de altas energías, aun cuando físicamente los valores observados son finitos. Esto parece un problema asociado con el uso de series perturbativas, y supuestamente algunos métodos no perturbativos no conocidos resolverían el problema. Por lo tanto, la renormalización es necesaria ya que hoy en día no se conoce cómo hacer los cálculos sin series perturbativas.
Introducción[editar]
Estos procedimientos tienen que ver con los problemas que surgen de pasar a un límite continuo y tienen que ver con la autointeracción de un campo consigo mismo. Más concretamente, cuando se describe un sistema físico de manera aproximada mediante una red discreta de puntos ciertas cantidades están bien definidas, sin embargo, al pasar al límite continuo de forma "cruda" considerando una infinidad de puntos, las cantidades están mal definidas matemáticamente. Es decir, sobre un espacio-tiempo definido como una retícula de puntos numerable, la teoría da resultados finitos pero al hacer disminuir la distancia mínima entre puntos hacia cero, algunos términos se disparan a infinito. La renormalización consiste en un conjunto de procedimientos de calcular el límite continuo de manera alternativa de manera que todas las cantidades estén bien definidas y no den lugar a términos infinitos.
Cuánticamente no resulta posible medir el valor del campo con infinita precisión en un punto del espacio, sino solo en una región muy pequeña pero no de volumen nulo. De hecho la magnitud observable ligada a un campo físico es una distribución definida sobre funciones de soporte compacto cuyos valores son operadores de campo. En el caso de teorías de campo libre (sin autointeracciones) este hecho no causa problemas serios y se puede construir un formalismo no perturbativo. Sin embargo, para un campo con interacción nadie sabe cómo formular una teoría exacta del campo, por lo que el procedimiento común es considerar un desarrollo perturbativo respecto a la teoría del campo libre (sin interacción).[1] Y en ese caso, resulta inevitable considerar productos de operadores de campo en el mismo punto del espacio, lo cual es una operación que matemáticamente no está bien definida en todos los casos.
Teorías de gauge[editar]
Una propiedad importante de las teorías de campo recalibrado es que tienen la propiedad de ser renormalizables, es decir, existe una técnica bien definida que da lugar a términos finitos (además experimentalmente varias de estas teorías renormalizables se han comprobado no solo correctas sino numéricamente muy precisas). El hecho de que se tenga un procedimiento claro de renormalización para teorías de recalibración, ha hecho que este tipo de teorías de campo hayan sido extensivamente estudiados, ya que mediante renormalización permiten obtener respuestas finitas contrastables con los experimentos.
La renormalización determina la relación entre los parámetros de la teoría, cuando los parámetros que describen el comportamiento para grandes distancias difieren del los parámetros que describen el comportamiento a pequeñas distancias. La renormalización fue desarrollada inicialmente para la electrodinámica cuántica (QED) con el objetivo de dar sentido a los valores infinitos de ciertas integrales obtenidas mediante teoría de perturbaciones a partir del caso del campo libre. Si bien inicialmente, se vio como un procedimiento sospechoso, y físicos como Paul Dirac la criticaron, por lo que fue visto como un procedimiento no riguroso y provisional, con el tiempo la propiedad de ser renormalizable por dicho procedimiento acabó siendo considerado como un importante indicio de la autoconsistencia y adecuación de una teoría de campos, tanto desde el punto de vista físico como matemático.
Planteamiento e historia del problema[editar]
Autointeracción en física clásica[editar]
El problema de la aparición de infinitos debido a la autointeracción ya surgió en ciertos problemas de elecrodinámica clásica de partículas puntuales a finales del siglo XIX y principios del siglo XX. De acuerdo con la teoría de la relatividad especial se pensó que la masa de una partícula cargada debería incluir la masa-energía del campo electroestático (masa electromagnética). Asumiendo que la partícula es una cáscara esférica cargada de radio re, la masa energía del campo es:
Esta masa tiende a infinito en el límite re → 0. Esto implicaría que una partícula perfectamente puntual tendría una inercia infinita y por tanto no podría ser acelerada. El radio clásico del electrón es precisamente el valor de re para el cual la masa anterior coincide con la masa de un electrón, escogiendo además . Restaurando los factores c y la expresión del radio clásico viene dada por:
donde es la constante de estructura fina y es la longitud de onda Compton del electrón.
La masa total efectiva de una partícula esférica incluye la masa neta de la cáscara esférica (además de la masa anteriormente mencionada asociada a su campo eléctrico). Si se permite que la masa de la cáscara esférica sea negativa, sería posible desarrollar un punto límite consistente.[2] Esto es lo que se llama renormalización. H. Lorentz y M. Abraham intentaron desarrollar una teoría clásica de campos para el electrón, usando esa idea. Este trabajo pionero inspiró trabajos posteriores relacionados con la regularización y la renormalización en teoría cuántica de campos.
Cuando se calcula la interacción electromagnética entre partículas cargadas eléctricamente, resulta tentador ignorar la retrorreacción de una partícula del propio campo de la partícula sobre ella misma. Pero esta retrorreacción es necesaria para explicar el efecto de frenado de partículas cargadas que emiten radiación. Si se asume que el electrón es una partícula perfectamente puntual, el valor de la retrorreacción resulta infinito, y por la misma razón su masa electromagnética no es finita, porque el campo sigue una ley de la inversa del cuadrado.
La teoría de Abraham-Lorentz tiene consecuencias no causales conocidas como "preaceleración". A veces el electrón empieza a moverse antes de que la fuerza se aplique, esta característica es un signo de inconsistencia. El problema es peor en la electrodinámica clásica que en la electrodinámica cuántica, debido a que en el caso cuántico una partícula cargada experimenta un Zitterbewegung debido a la autointeracción con pares de partícula-antipartícula.
El caso de electrodinámica cuántica (QED)[editar]



La electrodinámica cuántica fue el primer caso exitoso de teoría cuántica de campos renormalizable y su desarrollo supuso la creación en paralelo de la idea de renormalización que luego fue aplicada a otras teorías cuánticas de campos. Cuando se desarrolló la electrodinámica cuántica durante los años 1930, Max Born, Werner Heisenberg, Pascual Jordan y Paul Dirac descubrieron que los cálculos perturbativos daban lugar a integrales que divergían a infinito.
La manera de describir esas divergencias se basó en el trabajo de Ernst Stueckelberg (ya en los años 1930), y casi una década más tarde por Julian Schwinger, Richard Feynman, y Shin'ichiro Tomonaga. Finalmente todos estos trabajos fueron sistematizados por Freeman Dyson. Las divergencias aparecen en los cálculos basados en diagramas de Feynman con ciclos cerrados (closed loops) asociados a partículas virtuales de la teoría. Aunque estas partículas virtuales obedecen las leyes de conservación de la energía y la cantidad de movimiento, pueden asumir cualquier energía y momento, incluso un valor que no está permitido por la relación relativista momento-energía (es decir, no es exactamente igual a la masa de la partícula que participa en dicho proceso. Así por ejemplo, para un fotón virtual la cantidad anterior podría no ser cero, lo cual equivale a que tuviera masa. Una partícula con una relación anómala entre energía y momento se denomina partícula off-shell (ya que en el espacio cuatridimensional formado por solo una "cáscara" (shell) de puntos satisface la relación ).
Cuando existe un ciclo cerrado o loop, el momento de las partículas que participan en dicho ciclo cerrado no viene unívocamente determinada por las energías y los momentos de las partículas reales entrantes y salientes (se supone que la interacción está localizada en una región compacta del espacio tiempo, y las partículas entrantes son las que llegan a ella y las salientes las que emergen de ella). Una variación en la energía de una de las partículas del ciclo cerrado puede ser compensada por una variación igual y opuesta en la energía de otras partícula del ciclo cerrado. Así para encontrar la amplitud del proceso cíclico uno debe considerar la operación de integración sobre todas las posibles combinaciones de valores de la energía y el momento que pueden viajar a lo largo del ciclo cerrado.
Estas integrales frecuentemente son divergentes, es decir, no dan lugar a un valor finito en un cálculo directo. Las divergencias que son significativas son las divergencias ultravioletas (UV). Una divergencia ultravioleta puede describirse como una que es resultado de:
- la región de integración donde las partícuas del ciclo tienen un momento y una energía muy demasiado grandes.
- una longitud de onda extremadamente corta y frecuencia muy alta de las fluctuaciones de los campos físicos, en la integral de camino del campo.
- un tiempo propio muy corto entre la emisión y la reabsorción, si el ciclo se piensa como una suma sobre las trayectorias de las partículas.
Por tanto, estas divergencias implican fenómenos que se dan a lo largo de distancias muy pequeñas y tiempos muy cortos. En QED existen exactamente tres diagramas con ciclos cerrados divergentes[3]
- Un fotón crea un par virtual electrón-positrón que se autoaniquila, este diagrama se denomina de polarización del vacío.
- Un electrón que rápidamente emite y reabsorbe un fotón virtual, llamado diagrama de autoenergía.
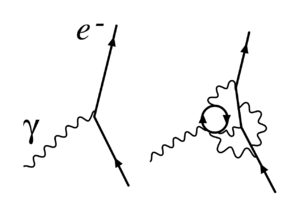
- Un electrón emite un fotón, emite un segundo fotón, y reabsorbe el primero. Este proceso se muestra en la figura, y se llama renormalización de vértice. El diagrama de Feynman para este caso también se llama diagrama pingüino debido a que su forma parece remótamente un pingüino (con el estado inicial y final de los electrones como los brazos y las piernas, el segundo fotón como el cuerpo y el primer fotón del ciclo como la cabeza).
Las tres divergencias corresponden a los tres parámetros de la teoría:
- la normalización del campo Z.
- la masa del electrón.
- la carga del electrón.
Una segunda clase de divergencia, llamada divergencia infrarroja, se debe a las partículas sin masa, como el fotón. Todo proceso en el que intervienen partículas cargadas emite infinitos fotones coherentes de longitud de onda infinita, y la amplitud para emitir cualquier número finito de fotones es cero. En el caso de los fotones, estas divergencias se conocen bien. Por ejemplo, en el orden de 1 bucle, la función de vértice tiene divergencias tanto en el ultravioleta como en el infrarrojo. En contraste con la divergencia ultravioleta, la divergencia infrarroja no requiere la renormalización de un parámetro en la teoría. La divergencia infrarroja del diagrama de vértice se elimina incluyendo un diagrama similar al diagrama de vértice con la siguiente diferencia importante: el fotón que conecta las dos patas del electrón se corta y se sustituye por dos fotones on shell (es decir, reales) cuyas longitudes de onda tienden a infinito; este diagrama es equivalente al proceso de bremsstrahlung. Este diagrama adicional debe incluirse porque no hay manera física de distinguir un fotón de energía cero que fluye a través de un bucle como en el diagrama de vértice y los fotones de energía cero emitidos a través de bremsstrahlung. Desde un punto de vista matemático las divergencias IR se pueden regularizar asumiendo una diferenciación fraccionaria con respecto a un parámetro, por ejemplo
está bien definido en p = a pero es una divergencia ultravioleta, si se toma la derivada fraccional de orden 3/2 con respecto a se obtiene una divergencia infrarroja:
por tanto, se pueden resolver las divergencias infrarrojas convirtiéndolas en divergencias ultravioletas.
Divergencia de un bucle[editar]
El diagrama de la Figura 2 muestra una de las varias contribuciones de un bucle a la dispersión electrón-electrón en QED. El electrón en el lado izquierdo del diagrama, representado por la línea sólida, comienza con cuatro momentos pμ y termina con cuatro momentos rμ. Emite un fotón virtual que lleva rμ − pμ para transferir energía y momento al otro electrón. Pero en este diagrama, antes de que eso suceda, emite otro fotón virtual que lleva cuatro momentos qμ, y reabsorbe este después de emitir el otro fotón virtual. La conservación de la energía y el momento no determina el cuatro momentos qμ de forma única, por lo que todas las posibilidades contribuyen por igual y debemos integrarnos. La amplitud de este diagrama termina con, entre otras cosas, un factor del bucle de
Las diferentes de esta expresión son matrices gamma como en la formulación covariante de la ecuación de Dirac; tienen que ver con el espín del electrón. Los factores de son la constante de acoplamiento eléctrico, mientras que la proporcionan una definición heurística del contorno de integración alrededor de los polos en el espacio de momenta. La parte importante para nuestros propósitos es la dependencia de qμ de los tres grandes factores en el integrando, que son del propagadors de las dos líneas de electrones y la línea de fotones en el bucle. Esto tiene una pieza con dos poderes de en la parte superior que domina en valores grandes de qμ (Pokorski 1987, p. 122):
Esta integral es divergente e infinita a menos que la cortemos a energía finita y momento de alguna manera. Divergencias de bucle similares ocurren en otras teorías cuánticas de campos.
Cantidades renormalizadas y cantidades desnudas[editar]
La solución a los problemas anteriores consiste en apreciar que las cantidades que inicialmente aparecían en las fórmulas de la teoría (como en la fórmula del langrangiano), representan cosas como la carga y la masa del electrón, así como las normalizaciones de los propios campos cuánticos, no son de hecho las constantes físicas medidas en el laboratorio.
Véase también[editar]
Referencias[editar]
- ↑ R. M. Wald, chapter 14, p. 380
- ↑ «Copia archivada». Archivado desde el original el 6 de abril de 2014. Consultado el 12 de marzo de 2015.
- ↑ See ch. 10 of "An Introduction To Quantum Field Theory", Michael E. Peskin And Daniel V. Schroeder, Sarat Book House, 2005
Notas[editar]
- ↑ Aunque la "QCD reticular" y otras técnicas similares permiten desde inicios del siglo XXI cálculos no perturbativos efectivos para muchas magnitudes.
Bibliografía[editar]
- Kevin Costello (2011): Renormalization and Effective Field Theory, ISBN 978-0-8218-5288-0.
- Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.


















