Se le llama identidad notable , producto notable , producto especial , producto de interés práctico [ 1] fórmula de multiplicación abreviada [ 2] producto que cumple reglas fijas y cuyo resultado puede ser escrito por simple inspección, es decir, sin verificar la multiplicación.[ 3]
Cada producto notable corresponde a una fórmula de factorización . Por ejemplo, la factorización de una diferencia de cuadrados perfectos es un producto de dos binomios conjugados . Los productos notables son simplemente multiplicaciones especiales entre expresiones algebraicas las cuales sobresalen de las demás. Son llamados "notables" ya que se presentan con frecuencia en matemática.[ 1]
Factor común [ editar ] Visualización de la regla de factor común . Forma un nomon . El resultado de multiplicar un binomio
a
+
b
{\displaystyle a+b}
c
{\displaystyle c}
propiedad distributiva :
c
⋅
(
a
+
b
)
=
c
⋅
a
+
c
⋅
b
{\displaystyle c\cdot (a+b)=c\cdot a+c\cdot b\,}
En la figura adjunta se observa que el área del rectángulo es
c
(
a
+
b
)
{\displaystyle c(a+b)\,}
a
+
b
{\displaystyle a+b\,}
c
{\displaystyle c\,}
c
a
{\displaystyle ca\,}
c
b
{\displaystyle cb\,}
Cuadrado de un binomio [ editar ] Ilustración gráfica del binomio al cuadrado . Para elevar un binomio al cuadrado (es decir, multiplicarlo por sí mismo), se suman los cuadrados de cada término más el doble del producto de ellos, dando:
(
a
+
b
)
2
=
a
2
+
2
a
b
+
b
2
{\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}\,}
Demostración
(
a
+
b
)
2
=
(
a
+
b
)
⋅
(
a
+
b
)
=
(
a
+
b
)
⋅
a
+
(
a
+
b
)
⋅
b
{\displaystyle (a+b)^{2}=(a+b)\cdot (a+b)=(a+b)\cdot a+(a+b)\cdot b}
=
a
⋅
a
+
b
⋅
a
+
a
⋅
b
+
b
⋅
b
{\displaystyle =a\cdot a+b\cdot a+a\cdot b+b\cdot b}
=
a
2
+
2
⋅
a
⋅
b
+
b
2
{\displaystyle =a^{2}+2\cdot a\cdot b+b^{2}}
La expresión siguiente:
a
2
+
2
a
b
+
b
2
{\displaystyle a^{2}+2ab+b^{2}\;}
trinomio cuadrado perfecto .
Cuando el segundo término es negativo, la igualdad que se obtiene es:
(
a
−
b
)
2
=
a
2
−
2
a
b
+
b
2
{\displaystyle (a-b)^{2}=a^{2}-2ab+b^{2}\,}
Ejemplo:
(
2
x
−
3
y
)
2
=
(
2
x
)
2
−
2
(
2
x
)
(
3
y
)
+
(
3
y
)
2
{\displaystyle (2x-3y)^{2}=(2x)^{2}-2(2x)(3y)+(3y)^{2}\,}
Simplificando:
(
2
x
−
3
y
)
2
=
4
x
2
−
12
x
y
+
9
y
2
{\displaystyle (2x-3y)^{2}=4x^{2}-12xy+9y^{2}\,}
Producto de binomios con un término común [ editar ] Dos binomios con un término común [ editar ] Ilustración gráfica del producto de binomios con un término común. Para efectuar un producto de dos binomios con término común se tiene que identificar el término común, en este caso x , luego se aplica la fórmula siguiente:
(
x
+
a
)
(
x
+
b
)
=
x
2
+
(
a
+
b
)
x
+
a
b
{\displaystyle (x+a)(x+b)=x^{2}+(a+b)x+ab\,}
Demostración
(
x
+
a
)
⋅
(
x
+
b
)
=
(
x
+
a
)
x
+
(
x
+
a
)
b
=
(
x
⋅
x
+
a
⋅
x
)
+
(
x
⋅
b
+
a
⋅
b
)
=
{\displaystyle (x+a)\cdot (x+b)=(x+a)x+(x+a)b=(x\cdot x+a\cdot x)+(x\cdot b+a\cdot b)=}
x
⋅
x
+
a
⋅
x
+
x
⋅
b
+
a
⋅
b
=
{\displaystyle x\cdot x+a\cdot x+x\cdot b+a\cdot b=}
x
2
+
(
a
+
b
)
x
+
a
⋅
b
{\displaystyle x^{2}+(a+b)x+a\cdot b}
Ejemplo:
(
x
+
4
)
(
x
−
7
)
=
x
2
−
3
x
+
(
−
28
)
{\displaystyle (x+4)(x-7)=x^{2}-3x+(-28)\,}
(
2
y
−
1
)
(
2
y
−
3
)
=
(
2
y
)
2
+
(
−
1
−
3
)
(
2
y
)
+
(
(
−
1
)
(
−
3
)
)
=
4
y
2
−
8
y
+
3
{\displaystyle (2y-1)(2y-3)=(2y)^{2}+(-1-3)(2y)+((-1)(-3))=4y^{2}-8y+3}
Tres binomios con término común [ editar ] Fórmula general:
(
x
+
a
)
(
x
+
b
)
(
x
+
c
)
=
x
3
+
(
a
+
b
+
c
)
x
2
+
(
a
b
+
c
a
+
c
b
)
x
+
a
b
c
{\displaystyle (x+a)(x+b)(x+c)=x^{3}+(a+b+c)x^{2}+(ab+ca+cb)x+abc}
Binomios con un término común [ editar ] Fórmula general:
(
x
+
a
1
)
⋅
.
.
.
⋅
(
x
+
a
n
)
=
{\displaystyle (x+a_{1})\cdot ...\cdot (x+a_{n})=}
x
n
+
(
a
1
+
.
.
.
+
a
n
)
x
n
−
1
+
{\displaystyle x^{n}+(a_{1}+...+a_{n})x^{n-1}+}
(
(
a
1
a
2
+
a
1
a
3
+
.
.
.
+
a
1
a
n
)
+
{\displaystyle ((a_{1}a_{2}+a_{1}a_{3}+...+a_{1}a_{n})+}
(
a
2
a
3
+
.
.
.
+
a
2
a
n
)
+
{\displaystyle (a_{2}a_{3}+...+a_{2}a_{n})+}
.
.
.
+
{\displaystyle ...+}
(
a
n
−
1
a
n
)
)
x
n
−
2
+
{\displaystyle (a_{n-1}a_{n}))x^{n-2}+}
.
.
.
+
{\displaystyle ...+}
(
a
1
⋅
.
.
.
⋅
a
n
)
.
{\displaystyle (a_{1}\cdot ...\cdot a_{n}).}
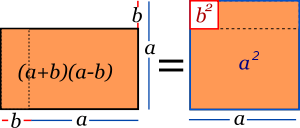
Producto de dos binomios conjugados [ editar ] Producto de binomios conjugados . Dos binomios conjugados se diferencian solo en el signo de la operación. Para su multiplicación basta elevar los monomios al cuadrado y restarlos (obviamente, un término conserva el signo negativo), con lo cual se obtiene una diferencia de cuadrados
(
a
+
b
)
(
a
−
b
)
=
a
2
−
b
2
{\displaystyle (a+b)(a-b)=a^{2}-b^{2}\,}
Ejemplo:
(
3
x
+
5
y
)
(
3
x
−
5
y
)
=
{\displaystyle (3x+5y)(3x-5y)=\,}
(
3
x
)
(
3
x
)
+
(
3
x
)
(
−
5
y
)
+
(
5
y
)
(
3
x
)
+
(
5
y
)
(
−
5
y
)
{\displaystyle (3x)(3x)+(3x)(-5y)+(5y)(3x)+(5y)(-5y)\,}
Agrupando términos:
(
3
x
+
5
y
)
(
3
x
−
5
y
)
=
9
x
2
−
25
y
2
{\displaystyle (3x+5y)(3x-5y)=9x^{2}-25y^{2}\,}
A este producto notable también se le conoce como suma por la diferencia
En el caso
(
p
−
a
+
b
+
c
)
(
p
−
a
−
b
−
c
)
=
(
p
−
a
)
2
−
(
b
+
c
)
2
{\displaystyle (p-a+b+c)(p-a-b-c)=(p-a)^{2}-(b+c)^{2}}
[ n 1] Cuadrado de un polinomio [ editar ] Elevación de un trinomio al cuadrado de forma gráfica. Para elevar un polinomio de cualquier cantidad de términos se suman los cuadrados de cada término individual y luego se añade el doble de la suma de los productos de cada posible par de términos.
(
a
+
b
+
c
)
2
=
a
2
+
b
2
+
c
2
+
2
(
a
b
+
a
c
+
b
c
)
{\displaystyle (a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2(ab+ac+bc)\,}
(
a
+
b
+
c
+
d
)
2
=
a
2
+
b
2
+
c
2
+
d
2
+
2
(
a
b
+
a
c
+
a
d
+
b
c
+
b
d
+
c
d
)
{\displaystyle (a+b+c+d)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+2(ab+ac+ad+bc+bd+cd)\,}
Ejemplo:
(
3
x
+
2
y
−
5
z
)
2
=
(
3
x
+
2
y
−
5
z
)
(
3
x
+
2
y
−
5
z
)
{\displaystyle (3x+2y-5z)^{2}=(3x+2y-5z)(3x+2y-5z)\,}
Multiplicando los monomios :
(
3
x
+
2
y
−
5
z
)
2
=
3
x
⋅
3
x
+
3
x
⋅
2
y
+
3
x
⋅
(
−
5
z
)
{\displaystyle (3x+2y-5z)^{2}=3x\cdot 3x+3x\cdot 2y+3x\cdot (-5z)\,}
+
2
y
⋅
3
x
+
2
y
⋅
2
y
+
2
y
⋅
(
−
5
z
)
{\displaystyle +2y\cdot 3x+2y\cdot 2y+2y\cdot (-5z)\,}
+
(
−
5
z
)
⋅
3
x
+
(
−
5
z
)
⋅
2
y
+
(
−
5
z
)
⋅
(
−
5
z
)
{\displaystyle +(-5z)\cdot 3x+(-5z)\cdot 2y+(-5z)\cdot (-5z)\,}
Agrupando términos:
(
3
x
+
2
y
−
5
z
)
2
=
9
x
2
+
4
y
2
+
25
z
2
+
2
(
6
x
y
−
15
x
z
−
10
y
z
)
{\displaystyle (3x+2y-5z)^{2}=9x^{2}+4y^{2}+25z^{2}+2(6xy-15xz-10yz)\,}
Luego:
(
3
x
+
2
y
−
5
z
)
2
=
9
x
2
+
4
y
2
+
25
z
2
+
12
x
y
−
30
x
z
−
20
y
z
{\displaystyle (3x+2y-5z)^{2}=9x^{2}+4y^{2}+25z^{2}+12xy-30xz-20yz\,}
Romper moldes
x
(
x
+
1
)
(
x
+
2
)
(
x
+
3
)
+
1
=
(
x
2
+
3
x
+
1
)
2
{\displaystyle x(x+1)(x+2)(x+3)+1=(x^{2}+3x+1)^{2}}
[ n 2] Cubo de un binomio [ editar ] Descomposición volumétrica del binomio al cubo. Para calcular el cubo de un binomio se suman, sucesivamente:
El cubo del primer término.
El triple producto del cuadrado del primero por el segundo.
El triple producto del primero por el cuadrado del segundo.
El cubo del segundo término.
(
a
+
b
)
3
=
a
3
+
3
a
2
b
+
3
a
b
2
+
b
3
{\displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\,}
Identidades de Cauchy:
(
a
+
b
)
3
=
a
3
+
b
3
+
3
a
b
(
a
+
b
)
{\displaystyle (a+b)^{3}=a^{3}+b^{3}+3ab(a+b)\,}
Ejemplo:
(
x
+
2
y
)
3
=
x
3
+
3
(
x
)
2
(
2
y
)
+
3
(
x
)
(
2
y
)
2
+
(
2
y
)
3
{\displaystyle (x+2y)^{3}=x^{3}+3(x)^{2}(2y)+3(x)(2y)^{2}+(2y)^{3}\,}
Agrupando términos:
(
x
+
2
y
)
3
=
x
3
+
6
x
2
y
+
12
x
y
2
+
8
y
3
{\displaystyle (x+2y)^{3}=x^{3}+6x^{2}y+12xy^{2}+8y^{3}\,}
Si la operación del binomio implica resta, el resultado es:
El cubo del primer término.
Menos el triple producto del cuadrado del primero por el segundo.Más el triple producto del primero por el cuadrado del segundo.Menos el cubo del segundo término.
(
a
−
b
)
3
=
a
3
−
3
a
2
b
+
3
a
b
2
−
b
3
{\displaystyle (a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}\,}
Identidades de Cauchy:
(
a
−
b
)
3
=
a
3
−
b
3
−
3
a
b
(
a
−
b
)
{\displaystyle (a-b)^{3}=a^{3}-b^{3}-3ab(a-b)\,}
Ejemplo:
(
x
−
2
y
)
3
=
x
3
−
3
(
x
)
2
(
2
y
)
+
3
(
x
)
(
2
y
)
2
−
(
2
y
)
3
{\displaystyle (x-2y)^{3}=x^{3}-3(x)^{2}(2y)+3(x)(2y)^{2}-(2y)^{3}\,}
Agrupando términos:
(
x
−
2
y
)
3
=
x
3
−
6
x
2
y
+
12
x
y
2
−
8
y
3
{\displaystyle (x-2y)^{3}=x^{3}-6x^{2}y+12xy^{2}-8y^{3}\,}
Identidad de Argand [ editar ]
(
x
2
+
x
+
1
)
(
x
2
−
x
+
1
)
=
x
4
+
x
2
+
1
{\displaystyle (x^{2}+x+1)(x^{2}-x+1)=x^{4}+x^{2}+1\,}
Identidades de Gauss [ editar ]
a
3
+
b
3
+
c
3
−
3
a
b
c
=
(
a
+
b
+
c
)
(
a
2
+
b
2
+
c
2
−
a
b
−
b
c
−
a
c
)
{\displaystyle a^{3}+b^{3}+c^{3}-3abc=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ac)\,}
a
3
+
b
3
+
c
3
−
3
a
b
c
=
1
2
(
a
+
b
+
c
)
[
(
a
−
b
)
2
+
(
b
−
c
)
2
+
(
a
−
c
)
2
]
{\displaystyle a^{3}+b^{3}+c^{3}-3abc={\frac {1}{2}}(a+b+c)[(a-b)^{2}+(b-c)^{2}+(a-c)^{2}]\,}
Identidades de Legendre [ editar ]
(
a
+
b
)
2
+
(
a
−
b
)
2
=
2
(
a
2
+
b
2
)
{\displaystyle (a+b)^{2}+(a-b)^{2}=2(a^{2}+b^{2})\,}
(
a
+
b
)
2
−
(
a
−
b
)
2
=
4
a
b
{\displaystyle (a+b)^{2}-(a-b)^{2}=4ab\,}
(
a
+
b
)
4
−
(
a
−
b
)
4
=
8
a
b
(
a
2
+
b
2
)
{\displaystyle (a+b)^{4}-(a-b)^{4}=8ab(a^{2}+b^{2})\,}
Identidades de Lagrange [ editar ]
(
a
2
+
b
2
)
(
x
2
+
y
2
)
=
(
a
x
+
b
y
)
2
+
(
a
y
−
b
x
)
2
{\displaystyle (a^{2}+b^{2})(x^{2}+y^{2})=(ax+by)^{2}+(ay-bx)^{2}\,}
(
a
2
+
b
2
+
c
2
)
(
x
2
+
y
2
+
z
2
)
=
(
a
x
+
b
y
+
c
z
)
2
+
(
a
y
−
b
x
)
2
+
(
a
z
−
c
x
)
2
+
(
b
z
−
c
y
)
2
{\displaystyle (a^{2}+b^{2}+c^{2})(x^{2}+y^{2}+z^{2})=(ax+by+cz)^{2}+(ay-bx)^{2}+(az-cx)^{2}+(bz-cy)^{2}\,}
Otras identidades [ editar ] Dado que la notabilidad de un producto es un concepto ambiguo, no existe una lista determinante que indique a cuáles productos se les puede considerar notables, y a cuáles no. A otras fórmulas, aunque menos usadas que las anteriores, en ciertos contextos se les puede calificar de productos notables . Entre ellas se destacan:
Adición de cubos:
a
3
+
b
3
=
(
a
+
b
)
(
a
2
−
a
b
+
b
2
)
{\displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})\,}
Diferencia de cubos:
a
3
−
b
3
=
(
a
−
b
)
(
a
2
+
a
b
+
b
2
)
{\displaystyle a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})\,}
factorización, ya que los productos no tienen una forma particularmente simétrica, pero el resultado sí (contrástese, por ejemplo, con la fórmula de binomio al cubo).
(
a
+
b
)
(
a
2
−
a
b
+
b
2
)
=
a
3
+
b
3
{\displaystyle (a+b)(a^{2}-ab+b^{2})=a^{3}+b^{3}\,}
(
a
−
b
)
(
a
2
+
a
b
+
b
2
)
=
a
3
−
b
3
{\displaystyle (a-b)(a^{2}+ab+b^{2})=a^{3}-b^{3}\,}
La suma y la diferencia de cubos se pueden generalizar a sumas y diferencias de potencias enésimas (o n - ésimas : xn ).
Suma de dos cuadrados
a
2
+
b
2
=
(
a
+
b
i
)
(
a
−
b
i
)
{\displaystyle a^{2}+b^{2}=(a+bi)(a-bi)\,}
Dónde i es la unidad imaginaria (√-1)
Demostración
(
a
+
b
i
)
(
a
−
b
i
)
=
a
2
−
(
b
i
)
2
=
a
2
−
(
b
2
⋅
i
2
)
=
a
2
−
(
b
2
(
−
1
)
)
=
a
2
−
(
−
b
2
)
=
a
2
+
b
2
{\displaystyle (a+bi)(a-bi)=a^{2}-(bi)^{2}=a^{2}-(b^{2}\cdot i^{2})=a^{2}-(b^{2}(-1))=a^{2}-(-b^{2})=a^{2}+b^{2}}
Suma de potencias enésimas:
Si –sólo si– n es impar,
a
n
+
b
n
=
(
a
+
b
)
(
a
n
−
1
−
a
n
−
2
b
+
a
n
−
3
b
2
−
⋯
+
b
n
−
1
)
{\displaystyle a^{n}+b^{n}=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^{2}-\cdots +b^{n-1})\,}
Diferencia de potencias enésimas:
a
n
−
b
n
=
(
a
−
b
)
(
a
n
−
1
+
a
n
−
2
b
+
a
n
−
3
b
2
+
⋯
+
b
n
−
1
)
{\displaystyle a^{n}-b^{n}=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^{2}+\cdots +b^{n-1})\,}
Las fórmulas de binomio al cuadrado y binomio al cubo se pueden generalizar mediante el teorema del binomio .
Para representar el cubo de un monomio, como diferencia de dos cuadrados , existe la siguiente fórmula[ 4]
a
3
=
(
(
a
+
1
)
a
2
)
2
−
(
(
a
−
1
)
a
2
)
2
{\displaystyle a^{3}=\left({\frac {(a+1)a}{2}}\right)^{2}-\left({\frac {(a-1)a}{2}}\right)^{2}}
Véase también [ editar ]
↑ Ya no se está ante binomios conjugados. El nombre clásico e histórico es «diferencia de cuadrados».
↑ Hay que multiplicar en el primer miembro. Luego tantear y poner como el cuadrado de un trinomio.
Referencias [ editar ] Bibliografía [ editar ] 


































































![{\displaystyle a^{3}+b^{3}+c^{3}-3abc={\frac {1}{2}}(a+b+c)[(a-b)^{2}+(b-c)^{2}+(a-c)^{2}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c861b04d0eb0a8d7e5f8bec4a258a7d9665049b4)













