Lógica temporal
La lógica temporal es una extensión de la lógica modal, la cual es prácticamente usada en sistemas de reglas, donde está presente el tiempo. Existe una cierta relación con otras variedades de lógica, por ejemplo, la lógica modal. Su estudio tiene importancia en la informática hasta nuestros días.
Por ejemplo, tomemos la sentencia: "Tengo hambre"; aunque su significado es independiente del tiempo, el valor de verdad o falsedad de la misma puede variar con el tiempo en un determinado sistema que incluya acciones de comer; así, en función del sistema, algunas veces será cierta y otras falsa, aunque nunca será cierta y falsa simultáneamente.
Historia[editar]
La lógica temporal fue estudiada por Aristóteles, en algunos de sus escritos hay expresiones que guardan una cierta analogía con la lógica temporal de primer orden; es de esta manera como aparecen expresiones con cuantificadores existenciales y cuantificadores universales
Sistemas basados en lógica temporal[editar]
En lógica temporal aparecen los mismos operadores que en una lógica de primer orden, junto con otros nuevos, entre los que se pueden encontrar: Siempre, algunas veces y nunca.
Algunos sistemas lógicos basados en lógica temporal son: Lógica computacional en árbol (Computational tree logic, CTL), lógica lineal temporal (Linear temporal logic, LTL) y Lógica temporal de intervalos (Interval temporal logic, ITL). Lógica de acciones temporal (Temporal Logic of Actions, TLA).
Operadores temporales[editar]
La lógica temporal tiene dos clases de operadores: operadores lógicos y operadores modales. Los operadores lógicos son usualmente operadores truth-functional (). Los operadores modales usan el Linear Temporal Logic y Computation Tree Logic son definidos como sigue.
| Textual | Símbólico | Definición | Explicación | Diagrama' |
| Operadores binarios | ||||
| U | Until: se cumple en el estado actual o uno posterior, y se tiene que cumplir hasta esa posición. A partir de esa posición no es necesario que se siga cumpliendo. |  | ||
| R | Release: releases si se cumple hasta que la primera posición en la cual se cumple (o siempre si dicha posición no existe). | 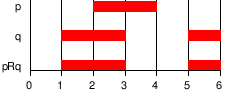 | ||
| Operadores unarios | ||||
| X | Next: se cumple en el siguiente estado. (X es usado como sinónimo.) |  | ||
| F | Finally: finalmente se cumple (en algún lugar del camino). |  | ||
| G | Globally: se tiene que cumplir en todo el camino. | 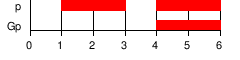 | ||
| A | All: se tiene que cumplir en todos los caminos empezando en el estado actual. | |||
| E | Exists: existe al menos un camino que parte en el estado actual en el cual se cumple. | |||
Símbolos alternativos:
- El operador R es algunas veces denotado por V
- El operador W es el operador weak until: es equivalente a
Operadores unarios son well-formed formulas cuandoquiera que B() es bien formado. Los operadores binarios son fórmulas bien formadas cuandoquiera que B() y C() son bien formadas.
En algunas lógicas, algunos operadores no pueden ser expresados. Por ejemplo, el operador N no puede ser expresado en la Temporal Logic of Actions.
Equivalencias[editar]
- donde V = verdadero
Ejemplo[editar]

En la figura se muestra una estructura de Kripke de tres estados. Se puede describir de la siguiente manera:
- En el estado rojo (eR) se cumple p, y hay transiciones hacia el resto de los estados.
- En el estado verde (eV) q es verdadero, y las transiciones van hacia el estado azul o el mismo estado.
- En el estado azul (eA) son verdaderas q y r, y tiene una única transición, hacia el estado verde.
Si se considera arbitrariamente al estado rojo como estado inicial, se cumple lo siguiente:
- EXr : pues tomando el camino eReAeVeV... , en el segundo estado (eA) r es verdadero, con lo que se encontró un camino que cumple Xr.
- AFq: pues para cualquier camino que se escoja inevitablemente habrá que entrar en los estados que hacen cumplir q, es decir, eV o eA.
Véase también[editar]
Bibliografía[editar]
- Venema, Yde, 2001, "Temporal Logic," in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic. Blackwell.
- E. A. Emerson and C. Lei, modalities for model checking: branching time logic strikes back, in Science of Computer Programming 8, p 275-306, 1987.
- E.A. Emerson, Temporal and modal logic, Handbook of Theoretical Computer Science, Chapter 16, the MIT Press, 1990
Enlaces externos[editar]
- Anthony Galton, Temporal Logic en la Stanford Encyclopedia of Philosophy.






















