Giróscopo

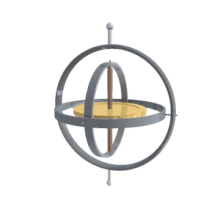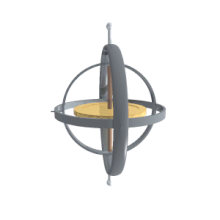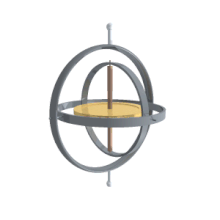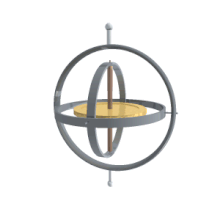
El giróscopo o giroscopio (del griego σκοπέω, skopeo, ‘ver’ y γῦρος, giros, ‘giro’) es un dispositivo mecánico que sirve para medir, mantener o cambiar la orientación en el espacio de algún aparato o vehículo.
Está formado esencialmente por un cuerpo con simetría de rotación que gira alrededor del eje de dicha simetría. Cuando el giróscopo se somete a un momento de fuerza que tiende a cambiar la orientación de su eje de rotación, tiene un comportamiento aparentemente paradójico, ya que cambia de orientación (o experimenta un momento angular en todo caso, si está restringido) girando respecto de un tercer eje, perpendicular tanto a aquel respecto del cual se lo ha empujado a girar, como a su eje de rotación inicial. Si está montado sobre un soporte de Cardano que minimiza cualquier momento angular externo, o si simplemente gira libre en el espacio, el giróscopo conserva la orientación de su eje de rotación ante fuerzas externas que tiendan a desviarlo mejor que un objeto no giratorio; se desvía mucho menos, y en una dirección diferente.
Presenta, por tanto, dos propiedades fundamentales: la inercia giroscópica o "rigidez en el espacio" y la precesión, que es la inclinación del eje en ángulo recto ante cualquier fuerza que tienda a cambiar el plano de rotación. Estas propiedades se manifiestan a todos los cuerpos en rotación, incluida la Tierra. El término giróscopo se aplica generalmente a objetos esféricos o en forma de disco montados sobre un eje, de forma que puedan girar libremente en cualquier dirección; estos instrumentos se emplean para demostrar las propiedades anteriores, para indicar movimientos en el espacio, o para producirlos.
Este fenómeno físico, el efecto giroscópico, puede observarse fácil y cotidianamente en peonzas, o monedas lanzadas a rodar, por ejemplo, aunque por supuesto, cualquier objeto giratorio funciona en cierto modo, como giróscopo. El giro en vuelo impartido por el jugador a un balón de rugby, o el de una bala disparada desde un arma de ánima rayada para estabilizar su trayectoria son ejemplos de aplicación del efecto.
Historia y aplicaciones[editar]

La peonza o trompo es seguramente el elemento cultural más viejo y sencillo que ilustra de forma clara el efecto giroscópico en funcionamiento. En sus diversas formas se conoce desde muy antiguo, con restos y referencias pictóricas o epigráficas que datan al menos desde el primer milenio a. C. en Mesopotamia, aunque seguramente sea muy anterior. Hay evidencias de su uso temprano en la Antigua Roma, en Grecia, China, India y muchos otros lugares. Permanece en esencia un juguete inalterado, variando ligeramente la forma, los materiales (arcilla, madera, plástico, metal, etc.) y la decoración. Por supuesto, conocer empíricamente su funcionamiento, el hecho de que al girar se mantiene en pie, no implica que se conociesen las causas del fenómeno, ni poder calcular la magnitud y los factores que influyen en el efecto, con lo que las aplicaciones más potentes no fueron evidentes hasta mucho más tarde, concluida la revolución científica y hacia el final de la Revolución Industrial.

Al parecer, uno de los primeros intentos conocidos de aplicación de las propiedades de la peonza fue el "espejillo giratorio" de John Serson, un capitán inglés. En 1743, inventó una especie de peonza que serviría para localizar el horizonte en alta mar, en condiciones de visibilidad reducida, gracias a su estabilidad dinámica. Sería un precursor muy rudimentario del horizonte artificial moderno, aunque no parece haber tenido gran impacto.
A quien se atribuye el descubrimiento del efecto giroscópico y la construcción del primer instrumento parecido al giróscopo moderno es al astrónomo alemán Johann Gottlieb Friedrich von Bohnenberger, quien en 1817 escribió acerca del tema en un escrito titulado Descripción de una máquina para la explicación de las leyes de rotación de la Tierra en torno a su eje, y del cambio de orientación del mismo. Llamó a su aparato, una esfera rotatoria pesada, "la máquina".[1] El matemático francés Siméon Denis Poisson ya menciona[2] dicha máquina en 1813, en una memoria suya, y su compatriota y colega Pierre-Simon Laplace, trabajando por aquel entonces en la escuela politécnica de París, recomendó su uso en la enseñanza, como ayuda didáctica. Así fue como llegó a saber de ella Léon Foucault.[3]
El giróscopo como tal fue inventado, con ese mismo nombre, en 1852 por Foucault, montando una masa rotatoria en un soporte de Cardano para un experimento de demostración de la rotación de la Tierra. La rotación ya había sido demostrada con el péndulo de Foucault. Sin embargo, la velocidad de rotación del péndulo es más lenta que la velocidad de rotación de la Tierra por un factor , donde representa la latitud en que se localiza el péndulo. Se necesitaba otro aparato para demostrar la rotación de la Tierra de forma más simple.

Foucault presentó así un aparato capaz de conservar una rotación suficientemente rápida (150 a 200 vueltas por segundo) durante un tiempo suficiente (una decena de minutos) para que se pudiesen hacer medidas. Esta proeza mecánica (para la época) ilustra el talento de Foucault y su colaborador Froment en mecánica.

Foucault también se dio cuenta de que su aparato podía servir para indicar el Norte. En efecto, si se impiden ciertos movimientos del soporte del giróscopo, este se alinea con el meridiano. Esto permitió la invención del girocompás, una brújula giroscópica.
Otra de sus aplicaciones industriales iniciales fue servir como sistema de guía a los primeros torpedos, permitiendo programar una rudimentaria ruta a seguir antes del lanzamiento y corregir, hasta cierto punto, las desviaciones sobre la marcha. En general se han empleado mucho para la navegación inercial en aviones, misiles y similares construidos antes de la aparición del GPS (aún son imprescindibles, pero ya no como único o principal sistema de guiado, sino para controlar con precisión la orientación). En este campo últimamente comienzan a sustituirse por giróscopos de fibra óptica, y en muchas aplicaciones industriales y cotidianas, como la tableta o el teléfono inteligente, se utilizan giróscopos del tipo "MEMS" (Micro Electro Mechanical System), "SMEM" en español, con menor tamaño y peso, y mayor precisión y sencillez, que solo comparten la función con el giróscopo mecánico, no el efecto giroscópico como principio operativo.
También se utilizan giróscopos mecánicos para disminuir el balanceo de navíos y para estabilizar plataformas de tiro.
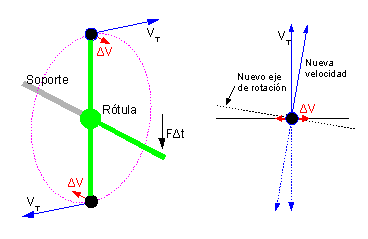
| Vista desde arriba del dibujo de la izquierda. Las velocidades de la masa de arriba están dibujadas en trazos continuos y las de la masa de abajo en punteado. |
Descripción del efecto giroscópico[editar]
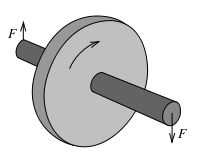
Supongamos un giróscopo formado por un disco montado sobre un eje horizontal, alrededor del cual el disco gira libremente a gran velocidad, como se observa en la figura de la derecha. Un observador mantiene el eje del fondo con la mano izquierda y el eje de delante con la mano derecha. Si el observador trata de hacer girar el eje hacia la derecha (bajando la mano derecha y subiendo la mano izquierda) sentirá un comportamiento muy curioso, ya que el giróscopo empuja su mano izquierda y tira de su mano derecha . El observador acaba de sentir el efecto giroscópico. Es una sensación muy sorprendente porque da la impresión de que el giróscopo no se comporta como un objeto «normal».
Descripción detallada del efecto[editar]
Las masas giran rápidamente alrededor del punto fijo con una velocidad tangencial . En el momento en que las masas pasan por la posición del dibujo se da un impulso hacia abajo en la extremidad libre de la T. La barra verde transmite ese impulso a las dos masas y le da a cada una, una pequeña velocidad horizontal perpendicular a su velocidad actual. Hacia la derecha en la masa de arriba y hacia la izquierda en la masa de abajo; es decir, la barra gira un poco respecto del eje longitudinal.
En el dibujo de la derecha aparecen las dos masas vistas desde arriba. Las velocidades comunicadas por el impulso se suman a las velocidades corrientes. La consecuencia inmediata es que la velocidad de la masa de arriba se desvía ligeramente hacia la derecha y la velocidad de la masa de abajo se desvía hacia la izquierda. Sorprendentemente, el resultado final es que el plano de rotación de las dos masas ha girado (aparte de respecto del eje longitudinal, también respecto del eje vertical) O, dicho de otra manera, el eje de rotación de las dos masas ha girado respecto de dos ejes, y no solo respecto del que intentábamos hacerlo girar.
En un giróscopo no se trata de dos masas puntuales sino de masas distribuidas sobre todo el disco o el cilindro, pero eso no cambia el fondo de la explicación. Y cuando, en lugar de darle un impulso a un giróscopo, se le aplica un momento, se puede considerar este momento como una sucesión de cortos impulsos. Cada uno de ellos añade a las masas una ínfima velocidad perpendicular a sus velocidades. Eso hace que la velocidad cambie de dirección sin cambiar de módulo.

Explicación intuitiva de la causa del efecto giroscópico[editar]
Supongamos frente a nosotros un giróscopo, un disco atravesado por un eje. Imaginémoslo de forma tal que el eje se encuentre en horizontal, frente a nuestros ojos, y nuestras dos manos agarren los extremos; por tanto, veremos el "canto" del disco en vertical. Imaginemos ahora que el disco comienza a girar en el sentido en el que su parte superior se "aleja" de nosotros y la inferior se "acerca" a nosotros. Imaginemos por ejemplo un punto rojo pintado sobre el canto, de modo que lo vemos girar con el disco, va siempre de abajo arriba al pasar frente a nosotros. Ahora subimos un poco nuestra mano izquierda y bajamos un poco la derecha, inclinando el eje de giro del disco. Si ahora miramos nuestro punto rojo, veremos que ya no viaja de abajo arriba, sino en diagonal, es decir, de abajo arriba y de izquierda a derecha. Ahora dividimos mentalmente el disco, sin detenerlo, en dos mitades: la más alejada de nosotros (la mitad del disco que no vemos, desde nuestra perspectiva) y la más cercana (la que vemos), y nos damos cuenta de que, en la parte más alejada del disco, el punto rojo viaja siempre hacia abajo y a la izquierda. En la más cercana, viaja hacia arriba y a la derecha. Por supuesto, no solo el punto rojo, toda la masa del disco sigue estas direcciones en cada mitad. La componente vertical del movimiento (arriba o abajo) podemos ignorarla, porque ya existía antes de inclinar el eje, aunque era mayor. Lo realmente nuevo son las componentes horizontales del movimiento. La masa se está desplazando de derecha a izquierda en la parte más alejada del disco, y de izquierda a derecha en la más cercana, en la que vemos. Estos movimientos de masa con una componente horizontal, que aparecen al inclinar el eje, originan reacciones (3.ª Ley de Newton) opuestas a ellos, y por tanto el disco experimentará una fuerza hacia la derecha en su parte alejada, y hacia la izquierda en su parte cercana. Es decir que nuestras manos, que sostienen el eje, al inclinarlo, subiendo la mano izquierda y bajando la derecha (además de notar la resistencia habitual de sentido opuesto a nuestro esfuerzo y que notaríamos aunque el disco no girase, 3.ª Ley de N), notarán una fuerza "extraña" que empuja hacia atrás nuestra mano derecha, y hacia delante la izquierda. Esta fuerza, sorprendente y desconcertante para quien no conoce el fenómeno, es el efecto giroscópico. Es por ese nuevo momento angular perpendicular al plano de rotación inicial por el que, si el giróscopo no está restringido en sus ejes de movimiento, al pretender girar dicho plano experimenta otra rotación (como reacción newtoniana a dicho momento) también en un tercer eje perpendicular al giro y a su eje de rotación inicial.
En resumen, la causa del efecto giroscópico es el cambio en la dirección de desplazamiento de la masa del disco, con una componente paralela al eje de rotación inicial, de sentido contrario en cada extremo del disco. Esta nueva componente del movimiento implica una reacción de sentido contrario (3.ª Ley de Newton), que se manifiesta en el momento angular que experimenta el giróscopo.

Esto se ve aún más claro si sustituímos el disco del giroscopio, una vez inclinado, por otros dos cuyos ejes de giro son ortogonales, como en las viñetas de la imagen de abajo. El disco vertical representa el momento angular que se conserva en el plano de giro inicial, y el horizontal el que ha pasado a este plano. Si el giroscopio permanece vertical, no hay rueda horizontal, solo equivale a un disco vertical de su mismo tamaño. Cuando comienza a inclinarse, aparece el disco horizontal, al principio muy pequeño, en comparación con el vertical. A medida que el giroscopio se va inclinando, y decrece el ángulo, el tamaño de la rueda vertical disminuiría, y aumentaría el de la horizontal. Es evidente que si las dos ruedas están acopladas en un único mecanismo, este experimentará un momento angular en el plano horizontal, contrario al sentido de giro del disco horizontal a medida que este crezca en tamaño (y por tanto en momento angular) para mantener la conservación del momento angular del mecanismo total.
Movimientos del giróscopo y planteamiento matemático[editar]
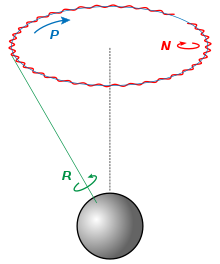
De acuerdo con la mecánica del sólido rígido, además de la rotación alrededor de su eje de simetría, un giróscopo presenta en general dos movimientos principales: la precesión y la nutación. Este hecho se deduce directamente de las ecuaciones de Euler.
Para entender cuantitativamente el movimiento de un giróscopo, podemos utilizar la segunda ley de Newton para la rotación.
Junto con las relaciones
y
Donde Ι es el momento de inercia y ω es la velocidad angular de la rueda respecto a su eje de spin.
En un giroscopio debemos tener en cuenta que el cambio en el momento angular de la rueda debe darse en la dirección del momento de la fuerza que actúa sobre la rueda.
La velocidad angular de precesión puede calcularse de la siguiente manera:
En un pequeño intervalo de tiempo dt, el cambio experimentado por el momento angular tiene módulo dL:
En donde MgD es el módulo del momento respecto al punto donde pivota. El ángulo θ barrido por el eje en su movimiento es
Y por lo tanto la velocidad angular de precesión es
Precesión[editar]

Cuando se aplica un momento a un cuerpo en rotación cuyo momento angular es , y siempre que no sea colineal con el momento angular original , la dirección del eje de rotación del cuerpo se anima de un movimiento de rotación de velocidad angular . Esta velocidad angular, llamada velocidad de precesión, está relacionada con el momento y el momento angular por la fórmula:
La velocidad de precesión, como todas las velocidades angulares, se mide en radianes/segundo. En módulo, la velocidad de precesión es igual a . Es decir, para una misma cantidad de momento, la magnitud de la velocidad de precesión es tanto más pequeña cuanto más grande sea el momento angular. Y como el momento angular es el producto de la velocidad de rotación del giróscopo multiplicada por su momento de inercia, se puede reducir la velocidad de precesión aumentando el momento de inercia, la velocidad de rotación o ambas.
Aquí encontramos el interés de utilizar un giróscopo para conservar una referencia de dirección. Partiendo del reposo, todos los cuerpos conservan la orientación que tienen salvo cuando se les aplican momentos externos. En ese caso, cuando un cuerpo no gira, el efecto del momento es el de crear una aceleración angular, la cual crea una velocidad angular creciente. Cuando el momento se interrumpe, el objeto sigue girando con la velocidad angular que adquirió. En cambio, cuando el mismo momento se aplica a un objeto en rotación, este comienza a girar con la velocidad de precesión calculada antes. Y cuando el momento se interrumpe, la precesión del objeto también se interrumpe. El resultado es que, en un giróscopo, los momentos parásitos tienen mucho menos efecto a largo plazo que en un objeto sin rotación. Además, se puede disminuir el efecto de esos momentos, aumentando el momento de inercia y la velocidad de rotación del giróscopo.
Nutación[editar]
Cuando el momento que causa la precesión cambia de valor, la velocidad de precesión también cambia de valor. Pero ese cambio no sucede instantáneamente. Hay un periodo de transición durante el cual el giróscopo «cede» un poquito al momento en la misma dirección que un objeto que no gira. Después el giróscopo recobra lo que había cedido, oscilando en la dirección del momento alrededor de la trayectoria de precesión final. Este movimiento de oscilación transitorio se llama nutación.
Si el cambio de valor de los momentos se prolonga, la nutación puede durar mucho. Es el caso de la Tierra. La atracción de la Luna y del Sol sobre el abombamiento de la Tierra en el ecuador es diferente entre el lado próximo y el lado lejano respecto al astro. Esa diferencia de atracción crea un momento, el cual causa la precesión de los equinoccios. Pero, como ni el Sol ni la Luna están en el plano del ecuador terrestre, el momento producido por estos astros cambia periódicamente y el movimiento de nutación de la Tierra no se amortigua.
-
Peonza. Precesión uniforme.
-
Peonza. Precesión con cambio de signo.
-
Peonza. Puntos con velocidad de precesión nula.
Bicicleta[editar]
Se ha supuesto durante mucho tiempo que el efecto giroscópico era el único o el principal fenómeno físico relacionado con el equilibrio de las bicicletas y motocicletas, aunque ha sido varias veces refutado.[4] La forma más sencilla de comprobar que el efecto giroscópico no aporta la mayor parte de su estabilidad a una bicicleta es compensarlo con giróscopos en las ruedas. El experimento ha sido realizado[5] y se ha comprobado que la bicicleta es perfectamente estable sin efecto giroscópico neto. Sin embargo, es imposible conducir una bicicleta con el manillar bloqueado, lo que demuestra que son las fuerzas centrífugas (en el sistema de referencia de la bicicleta) que aparecen al mover el manillar las que le confieren estabilidad. Una bicicleta o una motocicleta lanzadas en movimiento sin conductor, siguen avanzando sin caerse hasta que encuentren un obstáculo o que pierdan su impulso. La trayectoria será una espiral, un círculo o, raramente, una recta.

En el dibujo está representada una bicicleta en movimiento con el manillar derecho e inclinada un poco hacia la izquierda. El peso de la bicicleta crea un momento que tiende a inclinar aún más la bicicleta y a hacerla caer. Pero como la bicicleta avanza, la rueda de delante tiene un momento angular dirigido hacia la izquierda. La rueda de atrás también tiene un momento angular, pero la manera en la cual está sujeta no le permite tener efecto en el equilibrio de la bicicleta. Este momento crea una variación , dirigida hacia atrás, del momento angular de la rueda de delante. Esto quiere decir que la rueda de delante gira hacia la izquierda, como si se hubiese girado el manillar hacia la izquierda. La bicicleta comienza a voltear hacia la izquierda. Mientras el momento haga inclinarse más la bicicleta, el momento angular de la rueda de delante se inclinará hacia atrás, el manillar hacia la izquierda y el radio de la trayectoria de la bicicleta disminuirá.
Visto desde el sistema acelerado y no inercial de la bicicleta, el radio de rotación disminuye, lo cual aumenta la fuerza centrífuga. Esta fuerza centrífuga crea un momento que tiende a enderezar la bicicleta y a compensar el momento del peso que tiende a hacerla caer. Cuando los dos momentos terminan por compensarse, la bicicleta deja de inclinarse y el manillar de girar hacia la izquierda. La bicicleta continúa en su trayectoria circular con radio constante. Si el frotamiento con el aire u otras cosas disminuyen la velocidad de la bicicleta, la fuerza centrífuga disminuirá, la bicicleta recomenzará a caerse, lo cual hará girar el manillar hacia la izquierda. El radio de giro disminuirá, lo cual aumentará la fuerza centrífuga hasta que ésta compense de nuevo el momento del peso. Cuando el manillar llega a 90° o se bloquea, la bicicleta se cae.
Si se lanza una bicicleta con el manillar inmovilizado (amarrado), la bicicleta se caerá como si estuviese parada.
Véase también[editar]
Referencias[editar]
- ↑ Johann G. F. Bohnenberger (1817) "Beschreibung einer Maschine zur Erläuterung der Gesetze der Umdrehung der Erde um ihre Axe, und der Veränderung der Lage der letzteren" (Descripción de una máquina para la explicación de las leyes de rotación de la Tierra en torno a su eje, y del cambio de orientación del mismo), Tübinger Blätter für Naturwissenschaften und Arzneikunde, vol. 3, páginas 72–83.
- ↑ El matemático francés Poisson menciona la máquina de Bohnenberger ya en 1813: Simeon-Denis Poisson (1813) "Mémoire sur un cas particulier du mouvement de rotation des corps pesans" [Memoria sobre un caso particular del movimiento de rotación de los cuerpos pesados.], Journal de l'École Polytechnique, vol. 9, páginas 247–262. Disponible en Internet en: http://www.ion.org/museum/files/File_2.pdf .
- ↑ (En inglés) Wagner JF, "La Máquina de Bohnenberger", Instituto de la Navegación. (Wagner JF, "The Machine of Bohnenberger", The Institute of Navigation)
- ↑ Klein, Richard E.; et al. «Bicycle Science». Archivado desde el original el 10 de septiembre de 2007. Consultado el 4 de agosto de 2006.
- ↑ Jones, David E. H. (1970). «The stability of the bicycle» (PDF). Physics Today 23 (4): 34-40. Consultado el 4 de agosto de 2006.
Bibliografía[editar]
- Feynman, Leighton and Sands. Lectures on physics. Addison-Wesley. (en inglés)
Enlaces externos[editar]
 Wikimedia Commons alberga una galería multimedia sobre Giróscopo.
Wikimedia Commons alberga una galería multimedia sobre Giróscopo. Wikcionario tiene definiciones y otra información sobre giróscopo.
Wikcionario tiene definiciones y otra información sobre giróscopo. Wikcionario tiene definiciones y otra información sobre giroscopio.
Wikcionario tiene definiciones y otra información sobre giroscopio.- The Precession and Nutation of a Gyroscope. Archivado el 30 de marzo de 2010 en Wayback Machine. (en inglés)
- Everything you needed to know about gyroscopes (en inglés)
- Cómo construir giroscopios
- Magnetal AB - Giroscópico efecto y el volante - un estudio (en inglés)




















