Arco (geometría)

Arco, en geometría, es cualquier curva continua que une dos puntos.​ También, se denomina arco a un segmento de circunferencia; un arco de circunferencia queda definido por tres puntos, o dos puntos extremos y el radio, o por su cuerda.

Arco de una circunferencia.

Cálculo de la longitud de un arco

Métodos históricos

Antigüedad

A lo largo de la historia de las matemáticas, muchos grandes pensadores consideraron imposible calcular la longitud de un arco irregular. Arquímedes había descubierto un método por aproximación de rectángulos para calcular el área de un polígono curvilíneo mediante el método de exhausción, aunque pocos creyeron que era posible que una curva tuviese una longitud medible, como en las líneas rectas.

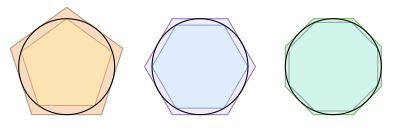
Las primeras mediciones se hicieron, como ya es común en el cálculo, a través de métodos de aproximación. Los matemáticos de la época empezaron a trazar polígonos dentro de la curva, y calculando la longitud de los lados de estos, obtenían la longitud aproximada de la curva. Mientras más segmentos se usaban, y se disminuía la longitud de cada segmento, se obtenía una aproximación cada vez mejor.

Método de exhausción: cálculo de la longitud de la circunferencia mediante la aproximación de polígonos inscritos y circunscritos.

Siglo XVII

En esta época, el método de agotamiento llevó a la rectificación por métodos geométricos de muchas curvas trascendentales: la espiral logarítmica por Torricelli en 1645 (algunos piensan que fue John Wallis en 1650); el cicloide por Christopher Wren en 1658, y la catenaria por Gottfried Leibniz en 1691.

Determinar la longitud de arco de un segmento irregular —también llamado rectificación de una curva— históricamente fue difícil. Aunque fueron utilizados varios métodos para curvas específicas, la llegada del cálculo trajo consigo fórmulas generales que daban soluciones concretas para algunos casos.

La longitud de un arco de circunferencia de radio r y ángulo θ (medido en radianes), con el centro en el origen, es igual a θr. Para un ángulo α, medido en grados, la longitud en radianes es α/180° × π, siendo la longitud de arco igual a (α/180°)πr.

Métodos modernos

Al considerar una función $f\left(x\right)$ y su respectiva derivada $f'\left(x\right)$, que son continuas en un intervalo [a, b], la longitud suya del arco delimitado por a y b es dada por la fórmula:

$s=\int _{a}^{b}{\sqrt {1+\left[f'\left(x\right)\right]^{2}}}\,dx$

Si la función está definida paramétricamente, donde $x=f\left(t\right)$ e $y=g\left(t\right)$:

$s=\int _{a}^{b}{\sqrt {\left[f'\left(t\right)\right]^{2}+\left[g'\left(t\right)\right]^{2}}}\,dt$

Si la función está en coordenadas polares, donde la coordenada radial y el ángulo están relacionados $r=f(\theta )$, la longitud de una curva se reduce a:

$s=\int _{a}^{b}{\sqrt {r^{2}+\left[{\frac {dr}{d\theta \ }}\right]^{2}}}\,d\theta \$

En la mayoría de los casos no hay una solución disponible y será necesario usar métodos de integración. Por ejemplo, aplicar esta fórmula a una elipse llevará a una integral elíptica de segundo orden.

Entre las curvas con soluciones conocidas están la circunferencia, catenaria, cicloide, espiral logarítmica y parábola.

Longitud de arco

La longitud de arco es una medida de la longitud de un arco de una curva cualquiera, si viene dada en coordenadas cartesianas la longitud de arco puede calcularse como:

$L_{a}=\int _{x_{1}}^{x_{2}}{\sqrt {1+f'(x)^{2}}}\ dx$

Si la curva viene especificada en coordenadas polares, la longitud entre el ángulo $\phi _{1}$ y $\phi _{2}$ viene dada por:

$L_{a}=\int _{\phi _{1}}^{\phi _{2}}{\sqrt {\rho '(\phi )^{2}+\rho (\phi )^{2}}}\ d\phi$

De esta última se deduce que para una circunferencia, dado que $\scriptstyle \rho (\phi )=R$ y $\scriptstyle \rho '(\phi )=0$, la longitud de arco puede expresarse sencillamente como:

$L_{a}=R(\phi _{2}-\phi _{1})\,$

Notas

Bibliografía

• Spiegel, Murray R.; Abellanas, Lorenzo (1992). McGraw-Hill, ed. Fórmulas y tablas de matemática aplicada. Aravaca (Madrid). ISBN 84-7615-197-7. 

Enlaces externos

• Arc, en mathworld

Véase también

• Método de exhausción
• Geometría diferencial de curvas en ℝ³